Día Internacional de la Mujer: Emmy Noether
- Detalles
- Categoría: Comsol
- Visto: 2840

Hoy se conmemora el día internacional de la mujer. Sin duda que han existido y existe un gran número de notables científicas e ingenieras. Sin embargo, en esta ocasión tomamos nota del trabajo de Emmy Noether, cuyo cumpleaños fue justamente en el mes de marzo, en 1882. Emmy nació en Erlangen, Alemania, y dedicó a su vida a las matemáticas. Sin embargo, su trabajo fue más allá, teniendo profundas implicancias en la física teórica. En pocas palabras, ya con su primer teorema conectó las matemáticas y la física, mostrando el vínculo entre la simetría en la naturaleza y las leyes universales de conservación [1]. ¿Qué implica esto? Es lo que pasamos a explicar ahora.
Algo de historia
Por el año 1900, no se admitían mujeres en las universidades. Por ello, Emmy tuvo que pedir la autorización a cada profesor para poder asistir a clases como oyente. En 1903 pasó los exámenes para estudiar en la Universidad de Gotinga, no obstante, sin poder inscribirse. El siguiente año se levantó la restricción y volvió Erlangen, donde obtuvo el Doctorado en Matemáticas en 1907. Desde 1908 a 1915 investigó en el instituto de matemáticas de Erlangen, sin sueldo ni nombramiento oficial, puesto que no se les permitía a las mujeres contratadas.
Con todo lo anterior en contra, Emmy (junto con David Hilbert y Felix Klein) estaba centrada en la Teoría General de la Relatividad, publicada por A. Einstein en 1915. Como grupo vieron un posible problema que posiblemente no se respetaban las leyes de la conservación de la energía. No obstante, Emmy utilizó su trabajo sobre la invariancia, donde teorizó que la energía de un objeto podría no conservarse localmente, pero la cantidad total no cambia durante una transformación. Su teorema establece que para cada simetría existe una ley de conservación correspondiente, lo que demuestra que las leyes de conservación de la física tienen sus raíces en la simetría matemática [1].
Impacto en la Física Teórica
Actualmente sabemos que la física se basa en ciertas reglas de conservación: conservación de la energía, cantidad del movimiento, etc. Si no existiera el teorema de Noether, todo lo que se puede decir es que se conservan, simplemente se dan. En cambio, con el Teorema de Noether, se puede decir que cada conservación surge de la simetría del espacio en el cual vivimos. Un espacio sin estas simetrías sería diferente e irreconocible del espacio que conocemos. De manera concreta, el teorema de Noether, probado por Emmy Noether en 1915, permite obtener cantidades conservadas a partir de simetrías en mecánica clásica, relativista y cuántica, etc, por mencionar algunas áreas de la física. Ejemplos:
- La simetría de traslación del tiempo resulta en la conservación de la energía.
- la simetría de traslación espacial da la conservación del momento lineal.
- la simetría de rotación lleva a la conservación del momento angular.
El significado de estos resultados va más lejos que cualquier elogio, puesto que, una teoría no llega a ser sólo lógica y precisa, sino que revela profundas verdades fundamentales sobre la naturaleza en forma de nuevos patrones, tocando la belleza misma.
Impacto en las matemáticas aplicadas e ingeniería
Los conceptos que trabajó o surgieron a partir del trabajo de Emmy llegaron muy lejos, incluso hasta nuestros días cuando abrimos la ventana de COMSOL Multiphysics. Por ejemplo, los conceptos de simetría. Una simetría de un objeto se produce cuando éste luce idéntico al observarlo desde perspectivas distintas. Existen varios tipos de simetrías como la simetría esférica, axial o reflexiva (ver Figura 1). La elección de la dimensión va a influir en cómo se tratan las ecuaciones que gobiernen el fenómeno de interés, y, por ende, las leyes de conservación.
Figura 1: Selección de la dimensión en COMSOL Multiphysics.
Otro ejemplo de los conceptos de Noether descrito en la sección anterior es el de la conservación de la energía, conservación del momento lineal y conservación del momento angular. En la Galería de Aplicaciones de COMSOL se encuentra el modelo tutorial que ilustra la conservación de energía cuando se utiliza la interfaz de física Thermoviscous Acoustics, Frequency Domain. El modelo en particular consiste en una pequeña configuración de prueba conceptual de un tubo principal con un resonador Helmholtz [2] (Figura 2).
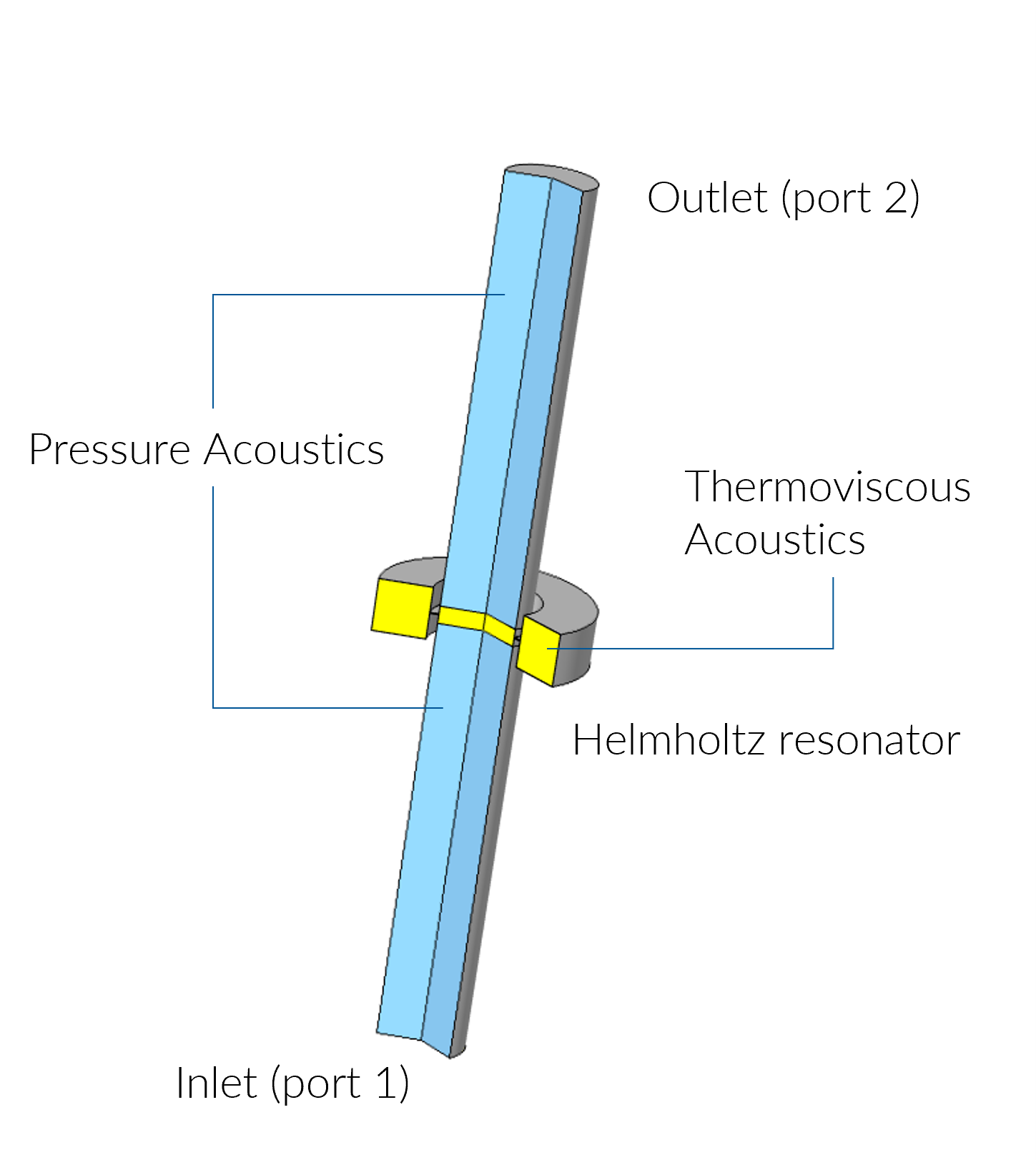
Figura 2: Geometría del resonador (ver [1]) en COMSOL Multiphysics.
Por otra parte, en el Blog de COMSOL sobre la dinámica de un giróscopo [3] se puede indagar sobre la conservación del momento angular (ver Figura 3). Un cuerpo giratorio quiere mantener la orientación de su eje en ausencia de momentos externos. La resistencia a cambiar de orientación cuando se perturba depende del momento angular, es decir, el producto de la velocidad angular y el momento de inercia asociado a la masa.
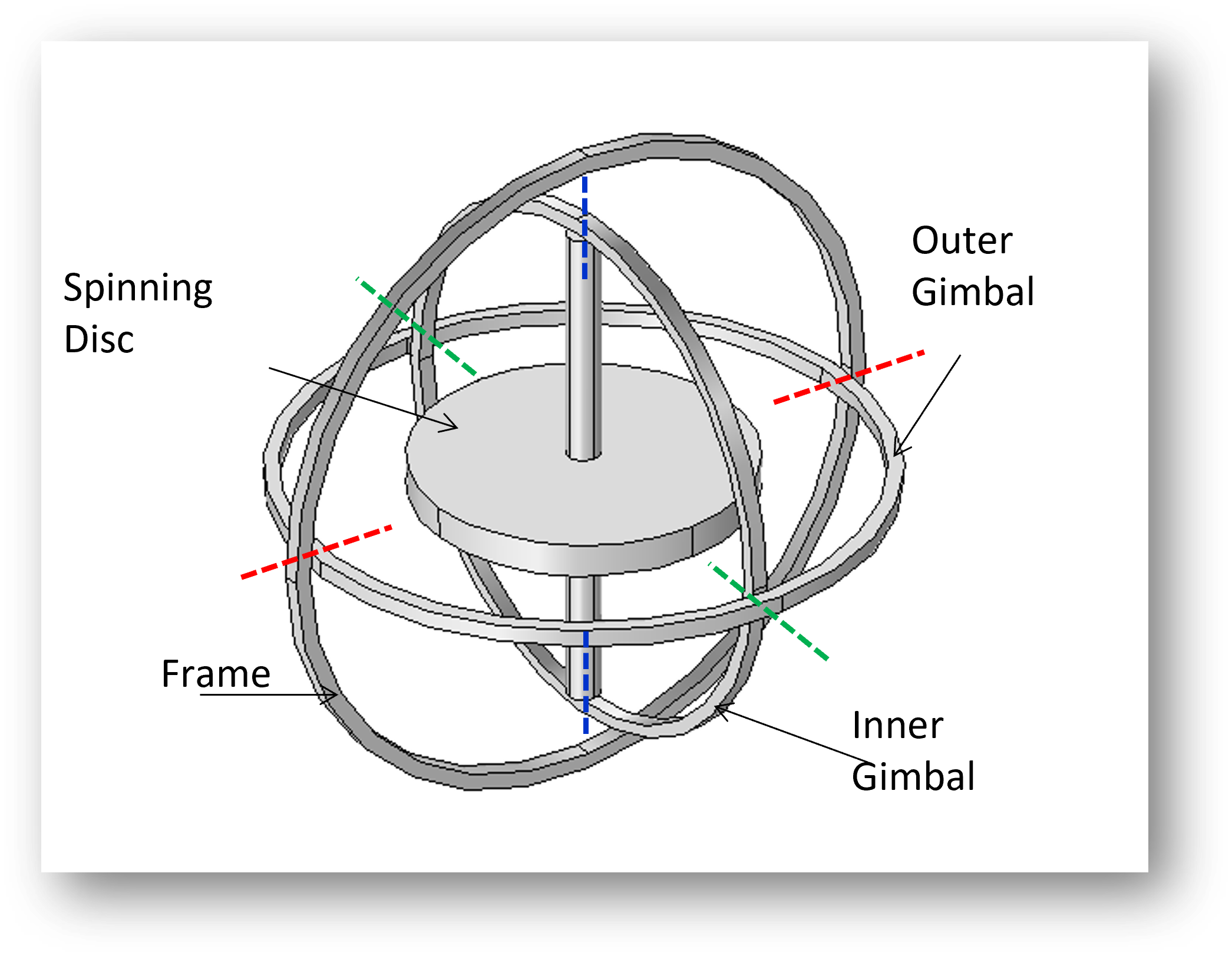
Figura 3: Geometría del giróscopo (ver [3]).
Referencias
[1]
[2]
[3]

