Modelado basado en Ecuaciones en COMSOL Multiphysics
- Detalles
- Categoría: Comsol
- Visto: 6647
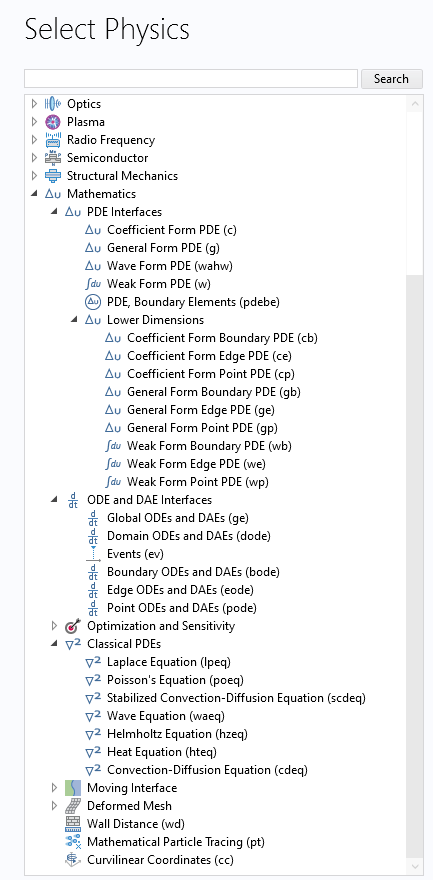
En COMSOL Multiphysics, la rama de Matemáticas contiene interfaces para resolver Ecuaciones en Derivadas Parciales (EDP), Ecuaciones Diferenciales Ordinarias (ODE) y Ecuaciones Diferenciales Algebraicas (DAE), realizar análisis de sensibilidad, modelar mallas móviles y geometrías deformadas, entre otras cosas. Dicha rama se encuentra en el Mathematics Module, que viene por defecto con la adquisición de la Licencia de COMSOL Multiphysics. Las diferentes interfaces son:
- PDE Interfaces: Resuelve EDP en forma de coeficiente, forma general y forma débil.
- ODE and DAE Interfaces: Permite añadir ecuaciones globales, ecuaciones independientes de la posición que representan otros estados.
- Optimization and Sensitivity: Permite la optimización (requiere Optimization module) y análisis de sensibilidad (por defecto en licencia básica).
- Classical PDE: Permite trabajar con casos especiales de EDP en forma de coeficientes. Dichas son la Ecuación de Laplace, Poisson, Ondas, Calor, Helmholtz, Convección-Difusión y Convección- Difusión Estabilizada.
- Deformed Mesh: Permite añadir estudios considerado una geometría deformada y de malla deformada como resultado de una carga.
- Wall Distance: Permite resolver la Ecuación de la eikonal para obtener la distancia a las paredes, lo cual se emplea en modelización de la turbulencia en fluido dinámica.
- Curvilinear Coordinates: Permite incorporar un sistema de coordenadas curvilíneo para definir propiedades de materiales del tipo anisotrópico, siguiendo la geometría de un objeto.
En esta ocasión nos centraremos en las EDP para dar una interpretación útil a los usuarios sobre cada término en la ecuación.
Las EDP y su interpretación
La EDP con una única variable dependiente u, en forma general en dominio Ω y sus condiciones de contorno en la frontera ∂Ω, se encuentran de la siguiente manera en la General Form PDE de COMSOL Multiphysics:
Los términos Γ, f, g, q, R y r son definidos por el usuario. Es decir, pueden ser funciones de las coordenadas espaciales, la solución u y las derivadas espaciales de u, así como otras variables definidas por el usuario. Los términos f, g, q, R y r son escalares. El término Γ es el vector de flujo.
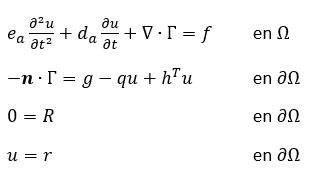
El vector Γ puede representar el flujo de una cantidad conservada, como calor, carga, masa o momento. Este flujo está usualmente relacionado mediante una ley material con el gradiente de la variable dependiente. Por lo tanto, Γ puede ser un vector cuyas componentes son funciones de las derivadas de la variable dependiente. El vector de flujo Γ puede también contener términos que son proporcionales a un campo de velocidad, cuando se tiene un transporte convectivo.
Las condiciones de contorno de la segunda línea de la ecuación corresponden a una condición de contorno tipo Neumann. Esta condición se denomina de flujo o fuente, debido a que especifica el valor del flujo numérico Γ en el contorno.
En la tercera y cuarta línea se tienen condiciones contorno del tipo Dirichlet. En el campo e los Elementos Finitos se les llama esenciales porque imponen una restricción en el espacio de prueba, que no es parte de la ecuación principal. La restricción de la tercera línea indica que una expresión arbitraria R es igual a cero en el contorno. La condición de Dirichlet de la línea 4 es un caso particular, especificando el valor de la variable dependiente en el contorno.
Forma de coeficientes
La forma de coeficientes de la EDP se encuentra de la siguiente manera en la Coefficient Form PDE interface de COMSOL Multiphysics. La primera línea de la ecuación es la EDP, que se cumple en el en el dominio Ω. Las ecuaciones en la segunda y tercera línea son las condiciones de contorno, que deben cumplir en ∂Ω. La segunda ecuación es una generalización de la condición de contorno de Neumann. La tercera ecuación es una restricción general, con la condición de contorno de Dirichlet como caso especial.
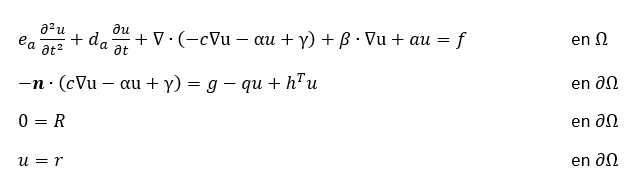
El usuario puede definir los coeficientes c, α, γ, β y a y los términos de contorno f, g, R y r. Cada uno de ellos pueden ser funciones de las coordenadas espaciales, así como variables dependientes y otras predeterminadas o variables definidas por el usuario y parámetros. Notar que para una única variable dependiente u, todos los coeficientes en la ecuación anterior son escalares excepto α, β y γ, que son vectores con 𝑛 componentes. El coeficiente c puede ser especificado como un escalar o como una matriz para materiales anisotrópicos.
Dualidad entre General Form y Coefficient Form PDE
La forma general y de coeficientes guardan una estrecha relación. En efecto, la forma de coeficientes es un caso particular de la forma general. Si se aplica una sustitución (ver ecuaciones siguientes) en la forma general, ésta se convierte en la forma de coeficientes. Este hecho da al usuario la posibilidad de escoger la representación en la que sea más sencillo trabajar una EDP.
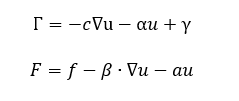
Una interpretación de los coeficientes de EDP

Ejemplos
Existen numerosos ejemplos de modelado basado en las interfaces del Mathematics Module. Por mencionar algunos que se encuentran disponible en el material de COMSOL tenemos: kdv equation-and solitons [1], Electrical Signals in a Heart [2] y A Lorenz Attractor [3]. Una breve descripción de cada modelo viene a continuación.
La Ecuación de Korteweg-de Vries (KdV) se creó en 1895 para modelar ondas de agua. Dado que la ecuación no introduce la disipación, las ondas viajan aparentemente para siempre. Estas ondas ahora se llaman solitones, que pueden viajar largas distancias sin alterar su forma o velocidad. Hoy, la ecuación KdV se usa para comprender las ondas de luz. Como resultado, una de las principales aplicaciones modernas de los solitones es en fibras ópticas (Figura 1).
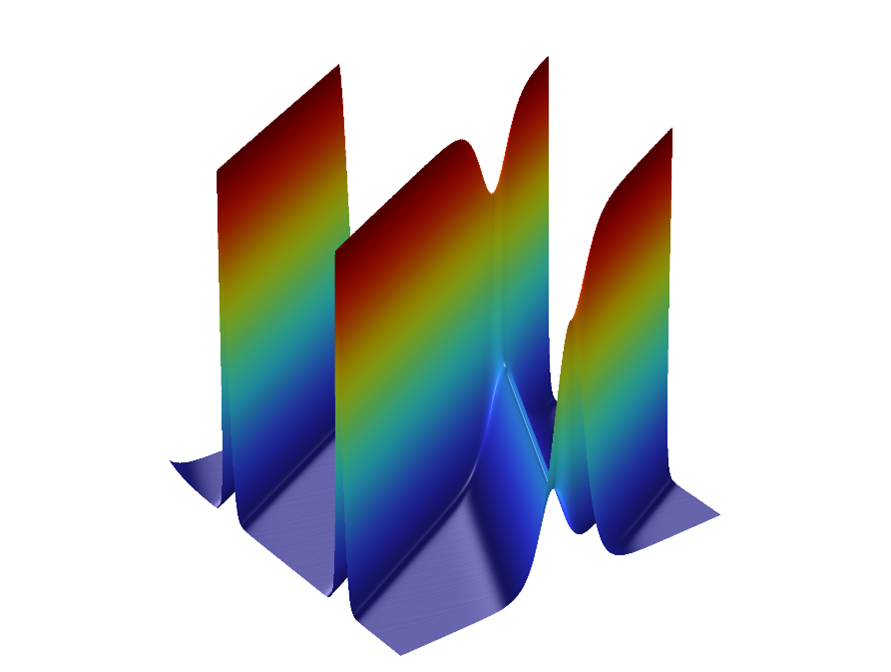
Figura 1: Resultado donde los solitones mantienen la forma intacta al colisionar, reapareciendo.
Modelar la actividad eléctrica en el tejido cardíaco es un paso importante para comprender los patrones de contracciones y dilataciones en el corazón. El corazón produce pulsos eléctricos rítmicos, que desencadenan las contracciones mecánicas del músculo. Varias afecciones cardíacas implican un riesgo elevado de reingreso de las señales. Esto significa que se altera el pulso constante normal, una condición grave y aguda que a menudo se denomina arritmia. La profesora Dra. Simonetta Filippi y el Dr. Christian Cherubini del Campus Universitario Biomédico di Roma, Italia, han proporcionado este modelo. En sí, son dos modelos matemáticos que describen diferentes aspectos de la propagación de la señal eléctrica en el tejido cardíaco: las ecuaciones de FitzHugh-Nagumo y las ecuaciones de Ginzburg-Landau, ambas resueltas en la misma geometría (Figura 2).

Figura 2: Solución de las ecuaciones de FitzHugh-Nagumo a 120 s.
Un atractor de Lorenz se puede describir mediante un sistema de ecuaciones diferenciales ordinarias (El sistema Lorenz). A principios de la década de 1960, Lorenz descubrió el comportamiento caótico de este sistema para ciertos valores de parámetros y condiciones iniciales. La solución, cuando se grafica como un espacio de fase, se asemeja a la Figura 3. Este ejemplo utiliza el método explícito de Dormand-Prince para resolver las ODE y un diagrama de trayectorias de puntos para visualizar el atractor de Lorenz.

Figura 3: Forma del Atractor de Lorenz.
Estos 3 modelos se encuentran en la Librería de Aplicaciones de COMSOL y además están descritos en el Blog de COMSOL Multiphysics [4].
Referencias
[1] https://www.comsol.com/model/the-kdv-equation-and-solitons-85
[2] https://www.comsol.com/model/electrical-signals-in-a-heart-981#:~:text=Modeling%20the%20electrical%20activity%20in,mechanical%20contractions%20of%20the%20muscle
[3] https://www.comsol.com/model/lorenz-attractor-16635
[4] https://www.comsol.com/blogs/3-examples-of-equation-based-modeling-in-comsol-multiphysics/

