Aspectos de los Elementos Finitos en COMSOL Multiphysics
- Detalles
- Categoría: Comsol
- Visto: 2860
Cuando se trabaja con una interfaz física en COMSOL, en la parte de ajustes, existe una sección de Discretización. Allí se puede escoger el orden de elemento que se está utilizando. Esta ocasión abordaremos el tema del orden de los elementos y la discretización para una simulación. Esta elección es importante porque tiene efectos en la malla y la solución del modelo.
¿Qué significan el orden y la discretización de los elementos?
La mayoría de las interfaces de física dentro de COMSOL Multiphysics utilizan el método de elementos finitos para resolver las ecuaciones diferenciales parciales subyacentes. El método de elementos finitos funciona discretizando los dominios de modelado en dominios más pequeños y simples llamados elementos. La solución se calcula ensamblando y resolviendo un conjunto de ecuaciones sobre todos los elementos del modelo. La solución de estas ecuaciones se aproxima a la solución real de la ecuación diferencial parcial.
Las ecuaciones dentro de cada elemento también se conocen como funciones de forma y pueden ser de distinto orden. Por ejemplo, en el caso más simple de un modelo de elementos finitos unidimensional, las funciones de forma dentro de cada elemento son simplemente un conjunto de polinomios definidos sobre el dominio. En la imagen siguiente se representa el conjunto de funciones de forma lineales (primer orden), cuadráticas (segundo orden) y cúbicas (tercer orden). La solución dentro de los elementos se basa en una suma lineal de estas funciones de forma. Ver Fig. 1.
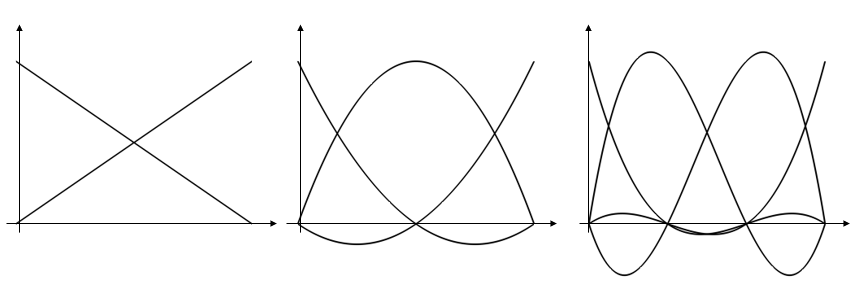
Fig. 1. Gráficos de funciones de forma lineal (izquierda), cuadrática (centro) y cúbica (derecha) en un elemento unidimensional (imagen obtenida del Blog de COMSOL [1]).
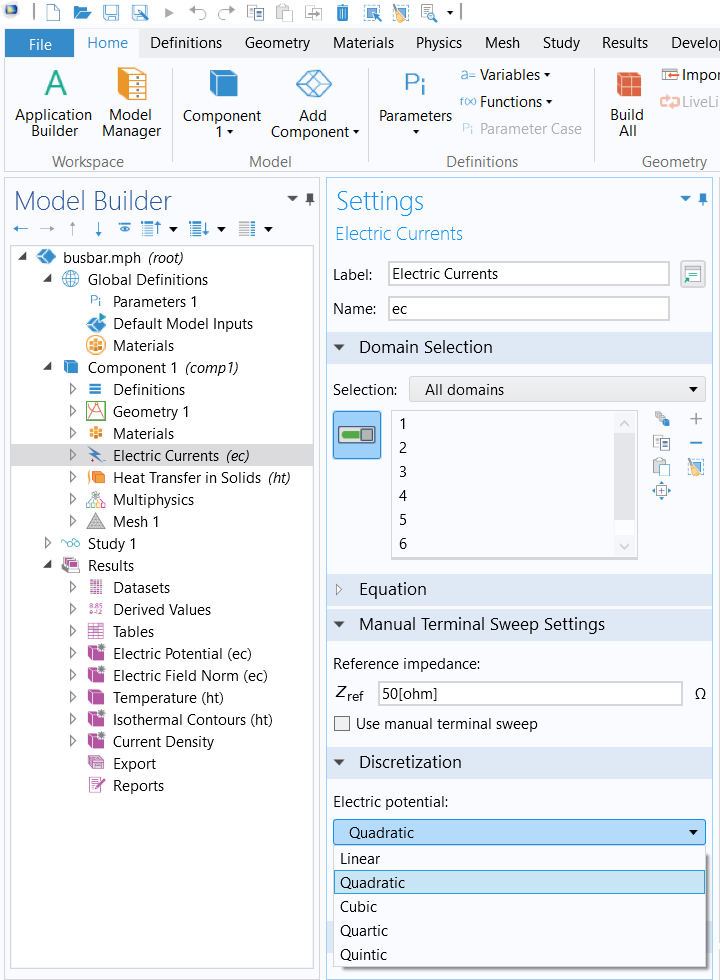
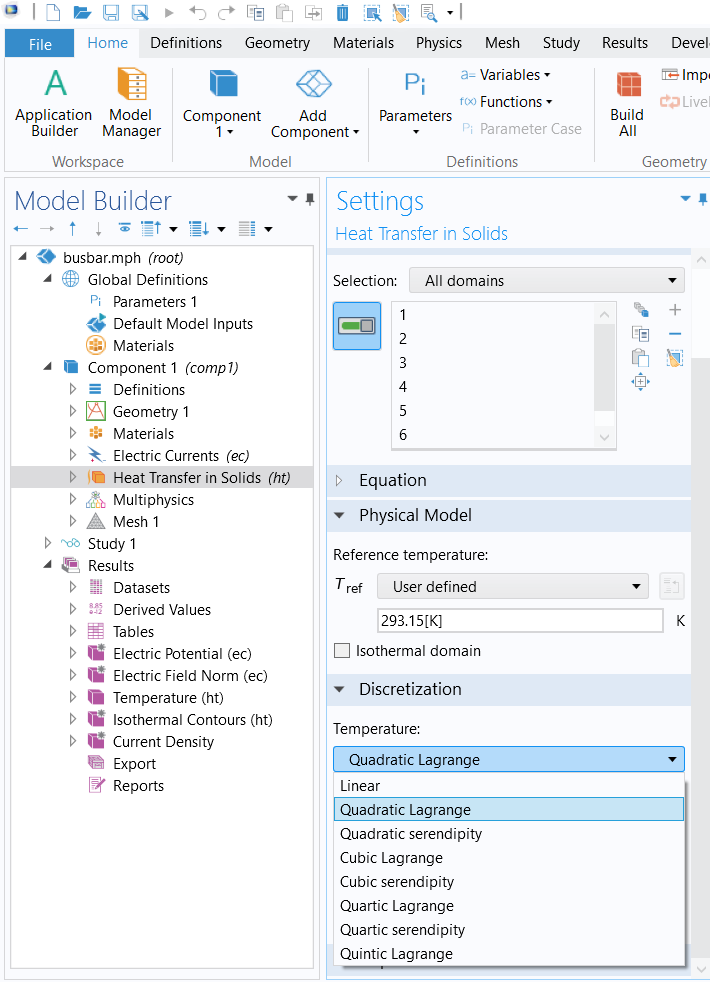
Un modelo que contiene varias interfaces físicas puede utilizar diferentes conjuntos de funciones de forma. Es decir, cada interfaz de física tiene sus propios ajustes de discretización únicos que gobiernan qué funciones de forma de orden se utilizan para esas variables dependientes, como se muestra en la captura de pantalla del ejemplo a continuación para la interfaz de física de Corrientes Eléctricas y Heat Transfer in Solids (Fig. 2).
 |
 |
|
Fig. 2. Funciones de forma utilizadas en el desplegable de discretización en la interfaz de Electric Currents (izquierda) y en la interfaz de Heat Transfer in Solids (derecha). En ambos casos se trata del modelo Busbar de la librería de aplicaciones. Ver [2]. |
|
La discretización por defecto en muchos casos es de segundo orden (cuadrática), y esto se debe en parte a que muchas de las ecuaciones diferenciales parciales tienen un término de segunda derivada dominante. Los problemas de flujo y transporte de fluidos suelen utilizar por defecto una discretización lineal de primer orden. Basado en la situación particular de modelado, cambiar la discretización puede estar motivado, y es posible cambiar la discretización para cada interfaz física diferente independientemente, pero hacerlo tiene varias consecuencias. Disminuir la discretización sin cambiar el número de elementos conducirá a un modelo que requiere menos recursos computacionales, pero tendrá menor precisión. Aumentar la discretización sin cambiar el número de elementos conducirá a una solución más precisa, pero requerirá mayores recursos computacionales. Se debe tener en cuenta que el aumento del orden de los elementos es un enfoque para validar el modelo, pero que es probable que desee estudiar el refinamiento de la malla mediante la realización de un estudio de refinamiento de malla.
Efecto en la malla
Al modelar en 2D, axis simétrico 2D o 3D, los ajustes de discretización dentro de la física también afectan a los elementos de malla. Los elementos de malla en 2D y 3D sirven además para aproximar la geometría CAD real, y lo hacen aproximando la forma de los contornos del modelo mediante un conjunto de funciones de forma geométrica que tienen el mismo orden que el orden de discretización más bajo utilizado en cualquiera de las interfaces de física habilitadas dentro del modelo.
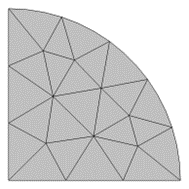
Lo anterior se puede visualizar considerando un dominio semicircular, discretizado con la malla más simple posible consistiendo en un único elemento triangular. Los lados rectos del dominio de modelado se representan con precisión sin importar las funciones de forma, pero el contorno curvo sólo puede representarse aproximadamente mediante las funciones de forma geométrica. Con una función de forma lineal, esta aproximación se reduce a un elemento triangular que representa bastante mal el dominio de modelización. Las funciones de forma cuadrática y cúbica ofrecen una representación mucho mejor de la geometría subyacente. Una consecuencia de esto es que, cuando se utilizan funciones de forma de geometría lineal, generalmente se necesita una malla mucho más fina en los límites curvos sólo para obtener una representación precisa de la geometría CAD subyacente.
De acuerdo con el Blog de COMSOL [3], una buena regla general, cuando se utilizan funciones de forma de geometría lineal, se necesitan al menos 8 elementos por arco de 90° para resolver el límite con menos del 1% de error. Por otro lado, con funciones de forma cuadráticas y de orden superior, incluso dos elementos por arco de 90° son suficientes para representar la geometría CAD con un error significativamente inferior al 1%. Estas reglas empíricas son sólo puntos de partida sobre cómo crear una malla inicial; siempre es necesario un estudio de refinamiento de la malla [3]. Notar que, al construir y visualizar la malla, los elementos aparecerán siempre con lados rectos, aunque las funciones de forma subyacentes sean de orden superior. Sólo cuando se trazan los resultados, los límites de los elementos se trazarán de forma que muestren la función de forma subyacente (ver Fig. 3)
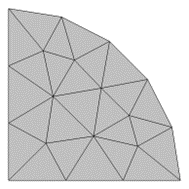 |
 |
|
Fig. 3. Se malla un dominio semicircular utilizando una función de forma lineal de Lagrange (izquierda) y Lagrange cúbica (derecha). Se observa la diferencia en la representación de la frontera curva. |
|
Más información sobre la inspección de los elementos de malla se puede ver en [4].
Referencias
[1]
[2]
[3]
[4]

