El diseño de experimentos (DOE) es una herramienta estadística muy eficaz y potente que puede ayudar a comprender y mejorar los procesos y diseñar mejores productos.

DOE permite evaluar los efectos principales de un proceso, así como los efectos de interacción (el efecto del factor A, por ejemplo, puede ser mucho mayor cuando el factor B se establece en un nivel específico, lo que lleva a una interacción). En ciencia y en negocios, necesitamos realizar experimentos para identificar los factores que tienen un efecto significativo. El objetivo del DOE es reducir los costes experimentales, la cantidad de pruebas, tanto como sea posible mientras se estudian tantos factores como sea posible para identificar los más importantes.

Fraccionamiento de un diseño

Supongamos que se necesitan estudiar los efectos de 6 factores de dos niveles en una respuesta. Un diseño factorial completo requeriría no menos de 64 ejecuciones. En la práctica, tener seis variables predictivas es muy común, pero ejecutar 64 pruebas es muy costoso y difícil de justificar. Es por eso que los diseños factoriales fraccionados se utilizan a menudo para reducir el número de ejecuciones en DOE de dos niveles. Los diseños factoriales fraccionarios son muy populares, y hacer una media fracción, un cuarto de fracción o una octava fracción de un diseño factorial completo puede reducir considerablemente los costes y el tiempo necesarios para un experimento.

Para estudiar 6 factores, se puede utilizar un diseño de 32 ejecuciones (media fracción del diseño completo), un diseño de 16 ejecuciones (fracción de cuarto) o incluso un diseño de 8 ejecuciones (octava fracción). En Minitab, se puede acceder rápidamente a la tabla de diseños factoriales que se muestra a continuación seleccionando Estadísticas> DOE> Factorial> Crear diseño factorial ... y haciendo clic en "Mostrar diseños disponibles".

Obsérvese que el diseño de 8 ejecuciones para estudiar los efectos de 6 factores de dos niveles está coloreado de rojo. Esto se debe a que se pagam un precio por reducir el número de ejecuciones de 64 a 8: se han generado alias (efectos confusos), por lo que la interpretación de los resultados se vuelve más difícil y arriesgada. En la tabla, rojo significa que algunos factores se confunden con interacciones de dos factores:

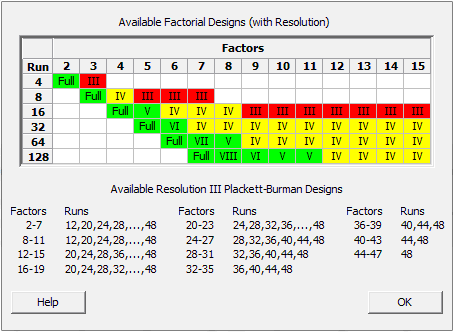
Diseño de resolución III

En un diseño de 8 carreras con seis factores, por ejemplo, el factor A se confunde con la interacción BD. Llamamos a esto un diseño de resolución III desde A = BD, lo que significa que tenemos tres elementos en esta cadena de alias. Un experimentador no puede separar sus efectos confusos: si el efecto de A o BD es significativo, no puede estar absolutamente seguro de si esto se debe al factor A o a la interacción BD.

¿Qué efectos e interacciones se confunden?

Cuando creas un diseño factorial fraccional, Minitab te dice qué efectos principales e interacciones se confunden con una estructura de alias y las "cadenas de alias" como éstas:

Generadores de diseño: D = AB, E = AC, F = BC

Estructura de alias

I + ABD + ACE + BCF + DEF + ABEF + ACDF + BCDE
A + BD + CE + BEF + CDF + ABCF + ADEF + ABCDE
B + AD + CF + AEF + CDE + ABCE + BDEF + ABCDF
C + AE + BF + ADF + BDE + ABCD + CDEF + ABCEF
D + AB + EF + ACF + BCE + ACDE + BCDF + ABDEF
E + AC + DF + ABF + BCD + ABDE + BCEF + ACDEF
F + BC + DE + ABE + ACD + ABDF + ACEF + BCDEF
AF + BE + CD + ABC + ADE + BDF + CEF + ABCDEF

Las interacciones de tres y cuatro factores (orden superior) rara vez son consideradas. ¿Por qué? Una interacción de tres factores, por ejemplo, significaría que el efecto de un factor se modifica al establecer otro factor, y que el efecto de esta interacción de dos factores se modificará al establecer un tercer factor. Este es un evento improbable y complejo, por lo que estas interacciones de orden superior no son tan preocupantes en un diseño fraccional.

Elegir un diseño fraccional apropiado

A veces, el precio que pagamos por una reducción en el número de pruebas es demasiado alto. Ese es el caso de los diseños de resolución III que se muestran en rojo arriba.

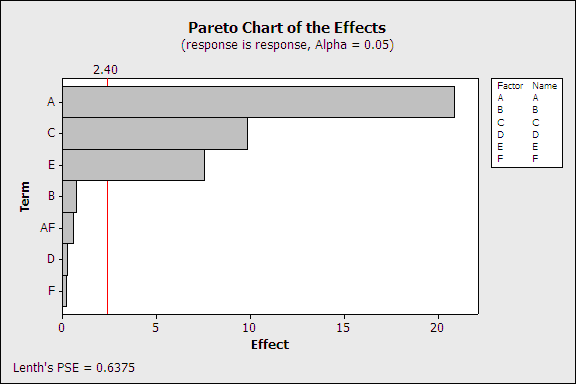
En el gráfico de efectos de Pareto, el factor A parece ser significativo (por encima del umbral de significación), pero A también se confunde con la interacción CE (por ejemplo). Solo se muestra A en el gráfico de Pareto, pero es solo el primer término de una larga cadena de alias:

A + BD + CE + BEF + CDF + ABCF + ADEF + ABCDE

 

Diseño de resolución IV

Los diseños amarillos en la tabla Diseños factoriales disponibles son mucho menos arriesgados. Estos diseños confunden las interacciones de dos factores con otras interacciones de dos factores. Por ejemplo, en un diseño factorial de 16 ejecuciones, 6 niveles de dos niveles, la interacción AB se confunde con la interacción CE. Este es un diseño de resolución IV, porque tenemos cuatro elementos en la cadena de alias AB = CE. De nuevo, no se pueden separar los efectos de AB y CE.

Estructura de alias

I + ABCE + ADEF + BCDF
A + BCE + DEF + ABCDF
B + ACE + CDF + ABDEF
C + ABE + BDF + ACDEF
D + AEF + BCF + ABCDE
E + ABC + ADF + BCDEF
F + ADE + BCD + ABCEF
AB + CE + ACDF + BDEF
AC + BE + ABDF + CDEF
AD + EF + ABCF + BCDE "
AE + BC + DF + ABCDEF
AF + DE + ABCD + BCEF
BD + CF + ABEF + ACDE
BF + CD + ABDE + ACEF
ABD + ACF + BEF + CDE
ABF + ACD + BDE + CEF

Aunque obviamente ya es menos arriesgado que los diseños de resolución III en rojo, este diseño de resolución IV (amarillo) no es tan arriesgado como podría parecer por dos razones:

• Efecto "Sparsity": por lo general, solo algunos de los muchos factores investigados eventualmente resultarán ser importantes (la "regla de Pareto").
• El principio de "herencia" (o "jerarquía"): cuando dos interacciones se confunden entre sí, la interacción que es más probable que sea significativa es la que contiene factores cuyos efectos principales son significativos en sí mismos.

Como consecuencia de esto, de los muchos factores que se investigan, se espera que solo unos pocos sean estadísticamente significativos y podemos centrarnos en las interacciones que contienen factores cuyos efectos principales son importantes en sí mismos. En esta etapa, también tendremos una mejor comprensión de nuestro proceso desde un punto de vista físico. Saber qué factores tienen un efecto real nos ayudará a determinar qué interacciones son más probables.

En un diseño de resolución IV, las interacciones de dos factores no se confunden con ningún efecto principal, por lo que este diseño es mucho más seguro que un diseño de resolución III, y le permite estudiar hasta 8 factores en solo 16 ejecuciones: ¡una solución bastante rentable!

Doblando un diseño

Supongamos que, a pesar de todo esto, AB y CE están confundidos y todavía no estamos realmente seguros de qué interacción es significativa. Realmente queremos separar los efectos de las interacciones AB y CE, y creemos que AB es tan probable que sea tan importante como CE. Quizás todos o ninguno de los efectos principales de A, B, C y E sean significativos, en cuyo caso el principio de "herencia" no será útil.

Como solución de último recurso, podríamos realizar pruebas adicionales para separar las interacciones confusas. En Minitab, iríamos a Estadísticas> DOE> Modificar diseño:

 

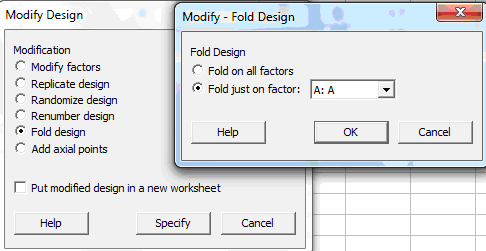
Esto aumentará el diseño inicial del DOE al agregar pruebas de seguimiento (un diseño "plegado"). Si el diseño inicial tenía 16 ejecuciones, será necesario agregar 16 ejecuciones plegadas para obtener un diseño en el que las interacciones AB y CE se puedan analizar por separado. Plegado significa que la serie adicional de pruebas será similar al DOE inicial. La sección de seguimiento es una imagen de espejo de la serie inicial de pruebas, excepto que el nivel de un factor (o de todos los factores) se cambiará sistemáticamente en las pruebas "plegadas" posteriores.

Al “fraccionar” un diseño se reduce el número de pruebas. Al "plegar" una fracción, se duplica su tamaño para separar interacciones/efectos principales.

Si se necesita separar el AB de la interacción CE, puede plegarse en el factor A (o alternativamente en el factor B o en C o en E) para romper la "cadena de alias". El plegamiento de todos los factores puede separar todos los efectos principales de las interacciones de dos factores cuando se ha realizado un diseño de resolución III (que se muestra en la zona roja de la tabla Diseños factoriales disponibles).

Incluso puede reducir la cantidad de pruebas de seguimiento adicionales para no duplicar la cantidad de pruebas doblando el diseño inicial, pero eso requiere técnicas más avanzadas.

Una estrategia segura para un DOE eficiente

Ningún diseño de experimentos está totalmente, 100%, libre de riesgos, pero esperamos convencer de que fraccionar y reducir el tamaño del diseño es una estrategia sensata y rentable. En la práctica, la fracción inicial casi siempre es suficiente por sí misma, pero si los resultados resultan ambiguos, como solución de último recurso, aún se puede modificar la fracción inicial y agregar una "fracción plegada".