La Universidad de Birmingham impulsa el aprendizaje utilizando herramientas digitales. Vea ejemplos de nuevos enfoques basados en la investigación y experiencia con la tecnología de Maplesoft.

La tecnología se expande a una rápida velocidad, revolucionando la forma en la que se accede a la información y se distribuye la educación. Esto proporciona a los educadores y estudiantes los beneficios de la conveniencia, facilidad de acceso, mayor interactividad y un uso más económico de los recursos. En el medio de estos beneficios, algunos se preguntan si la dependencia de las herramientas de aprendizaje en línea pone algún obstáculo a la eficiencia o si estas soluciones son capaces de cumplir todas las necesidades de aprendizaje de los estudiantes. Instructores de la Universidad de Birmingham en el Reino Unido han examinado estos asuntos a través de la introducción de herramientas en línea en su arsenal de enseñanza, y han dirigido preguntas y preocupaciones presentadas por educadores externos, para ilustrar cómo herramientas como Maple y Maple T.A. son realmente soluciones de aprendizaje efectivas.

La Universidad de Birmingham implementó Maple T.A. hace varios años, mejorando en gran medida las iniciativas de aprendizaje y enseñanza en la escuela, lo que incluye programas de pregrado y postgrado en asignaturas de ciencias, tecnología, ingeniería y matemáticas (STEM). Maple T.A. es un potente sistema de aprendizaje y evaluación diseñado específicamente para cursos STEM, respaldado por la potencia de cálculo simbólico del motor de Maple. La universidad fue capaz de incrustar el software dentro de su sistema de gestión de aprendizaje (LMS) existente, CANVAS. Al ampliar de forma efectiva su LMS de forma que es capaz de entender las matemáticas, ahora pueden distribuir con mayor extensión y de forma más robusta aprendizajes y evaluaciones de cursos basados en matemáticas.

Además de Maple y Maple T.A., la escuela recientemente adoptó Möbius, el material didáctico STEM completo, en línea, de Maplesoft. Möbius fue introducido en la universidad por el Dr. Tim Jackson para simplificar su curso de ingeniería de primer año, y actualmente existe un grupo de internos en la escuela comprobando las posibilidades de Möbius y trabajando con el profesorado para desarrollar contenido.

El Dr. Jonathan Watkins, un investigador y graduado de doctorado de la Universidad de Birmingham, fue una de las fuerzas creativas detrás de la integración de Maple T.A. con el LMS de la escuela. También fue responsable de la introducción del equipo de creación de contenidos de la escuela. Continúa trabajando con Maplesoft para mejorar el uso de la tecnología de Maplesoft en la escuela y proporcionar a los instructores el conocimiento para optimizar las capacidades de cada herramienta.

Nuevos enfoques

La Universidad de Birmingham adoptó Maple T.A. para mejorar la experiencia de aprendizaje de los estudiantes y optimizar el tiempo de los instructores para trabajar con los estudiantes. A medida que el profesorado se fue haciendo más familiar con las capacidades de Maple T.A., la Universidad decidió utilizar Maple T.A. en toda la universidad, no solo para proporcionar cursos con núcleo matemático. Como resultado, hicieron prioritario desarrollar sus propios contenidos para ajustarse a las necesidades individuales de todos sus estudiantes. Esto también les proporcionó la capacidad de controlar la calidad y cantidad, y asegurar que todos los materiales distribuidos se ajustaban a los altos estándares educaciones de la escuela.

Armados con contenidos personalizado y robusto, el personal introdujo nuevos enfoques a sus estilos de enseñanza y aprendizaje. A continuación se muestran dos ejemplos específicos que detallan cómo la universidad ha utilizado Maple T.A. para involucrar mejor a sus estudiantes y optimizar sus rutas de aprendizaje. El primer ejemplo ilustra cómo la universidad utilizó Maple T.A. para recompensar a los estudiantes por el proceso de llegar a una respuesta, no solo por la respuesta final. Esto anima a los estudiantes a pensar a través del problema y en cada paso para alcanzar la respuesta final. El segundo ejemplo muestra varios métodos introducidos para animar a los estudiantes a pensar más críticamente y desafiarse más para comprender conceptos matemáticos.

Parámetros de evaluación personalizados

Los miembros del grupo de creación de contenidos de Maple T.A. de la Universidad de Birmingham investigaron menearas de aplicar un mayor nivel de juicio humano a sus herramientas de evaluación, para proporcionar a los profesores un mayor control sobre los detalles y la calidad de las entradas que los estudiantes pueden proporcionar, así como la manera en que las pruebas y tareas son evaluadas en Maple T.A. Su equipo de contenidos trabajó con Maple T.A. para implementar maneras para reconocer los esfuerzos de los estudiantes y los procesos de pensamiento a medida que trabajan en la pregunta, más allá de la respuesta final.

Como un problema de ejemplo, los investigadores examinaron el gráfico de la Figura 1 más abajo. El gráfico se generó automáticamente utilizando Maple.

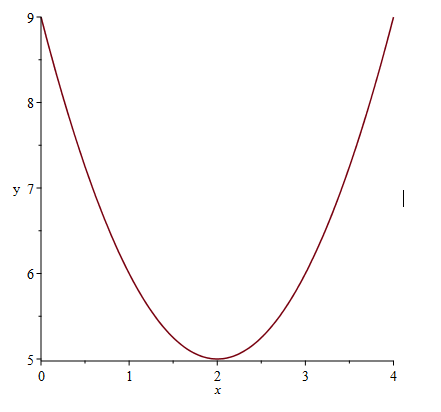
Figura 1. Gráfico generado por Maple

Para este gráfico, la forma de la respuesta puede especificarse en la pregunta como una lista [x, y]. Un estudiante puede identificar el mínimo como [2,5] pero igualmente pueden entrar [2.1, 4.9]. Ambos de estos intentos deben de ser recompensados igual, igual que si estuvieran marcados por una única persona.

Los pasos más abajo ilustran cómo crear esta pregunta en Maple T.A.

PASO 1

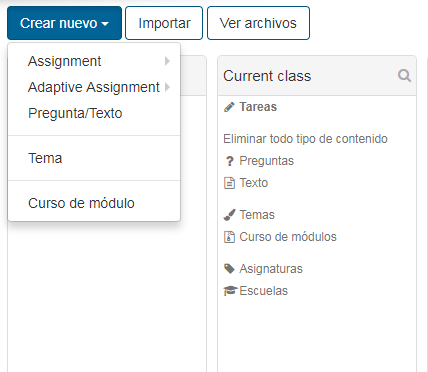
PASO 2

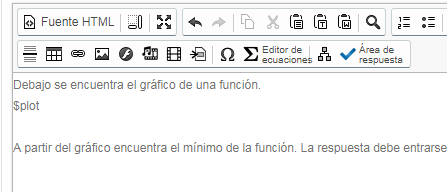
Los creadores de contenidos pueden entrar el texto de la pregunta, como se muestra más abajo. Para el área de respuesta, se escoge Maple-graded y se entra el código de evaluación como sigue:

evalb(abs($TA[1]-$RESPONSE[1]) < $abserr and abs($TA[2]-$RESPONSE[2]) < $abserr)

Se selecciona $TA como la respuesta y se escoge Maple syntax y “Text entry only”.

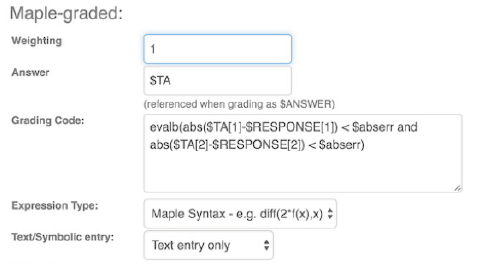
PASO 3

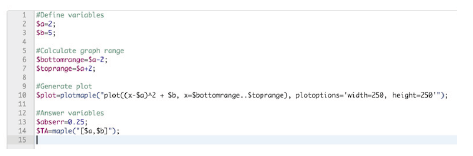
Se entra el algoritmo como sigue:

#Define variables
$a=2;
$b=5;
#Calculate graph range
$bottomrange=$a-2;
Stoprange=$a+2;
#Generate plot
$plot=plotmaple(“plot((x-$a)^2 + $b, x=$bottomrange..$toprange), plotoptions=’width=250, height=250’”);
#Answer variables
$abserr=0.25;
$TA=maple(“[$a,$b]”);

Ahora la pregunta está completada. Esto proporciona una ilustración de cómo los instructores que trabajan con Maple T.A. pueden estructurar las preguntas para que les proporcione un mayor grado de control sobre su evaluación de las respuestas de los estudiantes.

Cálculo de la comprensión conceptual

A medida que los estudiantes progresan en su educación pueden convertirse en adeptos en preparar pruebas y evaluaciones, y resolver los problemas que se les presentan. Sin embargo, la investigación ha mostrado que esto no es un indicador de la comprensión conceptual. En otras palabras, solo porque un estudiante pueda tener el conocimiento para resolver un problema no significa que realmente comprendan el concepto que existe detrás del problema en sí.

Durante el curso de un programa de grado, los estudiantes a menudo se hacen expertos en resolver problemas cuando se les proporciona los conjuntos de ecuaciones que necesitan resolver. Como la mayoría de instructores darán fe, la habilidad que a menudo les falta es la capacidad de producir este conjunto de ecuaciones en primer lugar. Con Maple T.A., es una tarea bastante trivial pedir a un estudiante que entre la solución a un sistema de ecuaciones y tener el sistema de verificación de que lo ha entrado correctamente. El Dr. Watkins encontró que muchos profesores con los que habló querían ser capaces de desafiar a sus alumnos a pensar más allá sobre los conceptos en sí mismo. Querían que sus estudiantes tuvieran la habilidad de proporcionar las ecuaciones gobernantes y las condiciones de contorno para un problema específico.

Maple T.A. permite a los instructores calcular la comprensión conceptual, utilizando su motor matemático único para verificar si los estudiantes son capaces o no de formar el sistema de ecuaciones por ellos mismos, además de resolverlo. Utilizando un flujo de Couette 2D como ejemplo, el Dr. Watkins exploró cómo Maple T.A. podría ser utilizado para configurar una pregunta que abordara estos objetivos. Un flujo de Couette es una configuración de dinámica de fluidos que consiste en el flujo de un líquido viscoso en el espacio entre dos superficies, una de las cuales se mueve tangencialmente en relación a la otra. La Figura 2 se creó utilizando el diseñador de preguntas de Maple T.A., que proporciona una interfaz uniforme para el diseño de preguntas y más flexibilidad sobre la disposición del texto de la pregunta presentada al estudiante.

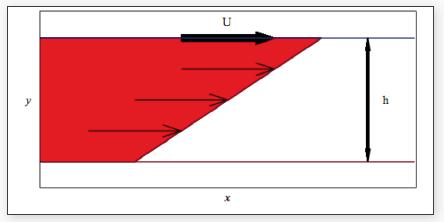
Figura 2. Flujo laminar de un líquido viscoso incompresible entre dos líneas paralelas

Al determinar el sistema de ecuaciones que especifica este sistema, los términos se pueden introducir como una lista separada por comas, seguida por la inserción de un cuadro de respuesta evaluado por Maple. Al utilizar el diseñador de preguntas, las respuestas a menudo son más largas que el ancho del cuadro de respuestas. Una manera de solucionarlo es cambiar el ancho de todas las cajas de entrada de una pregunta utilizando una etiqueta de estilo. Por ejemplo, uno puede hacer clic en el botón “source” del editor y entrar lo siguiente al principio de la pregunta:

<style id=”previewTextHidden” type=”text/css”>
input[type=”text”] {width:300px !important}
</style>

Aprentando “source” otra vez se mostrará el resultado de este cambio. El cuadro de entrada ahora será significativamente más ancho. Después necesitaremos añadir el algoritmo para esta pregunta. La respuesta del profesor para esta pregunta es el sistema de ecuaciones para el flujo de la figura:

$TA=”diff(u(y),y,y) = 0, u(0) = 0, u(h) = U”;
$sol=maple(“dsolve({$TA})”);

Es recomendable que los que desarrollen preguntas establezcan esto en $TA por consistencia entre preguntas. Para comprobar que existe una solución, utilice una llamada de Maple a la función dsolve de Maple, que devolverá la solución al sistema proporcionado de ecuaciones. Apretar refresco después de que el algoritmo realice estas operaciones y verifique la respuesta del instructor.

La parte clave de esta pregunta es el código de evaluación en el cuadro de respuesta evaluada por Maple. Añada el cuadro de respuesta al texto de la cuestión al final del texto que añadimos en el paso anterior. Haga clic en el área Insert Response y escoja el cuadro de respuesta evaluado por Maple en el menú de la izquierda. Para la respuesta, entre la variable $TA que definimos en el algoritmo. Para el código de evaluación, entre:

a:=dsolve({$RESPONSE}): evalb({$sol}={a})

Este código verifica que el sistema de ecuaciones del estudiante produce la misma solución que la del professor. Al preguntar la cuestión de esta manera se permite una respuesta más abierta del estudiante. Para finalizar asegúrese que el tipo de expresión es Maple syntax y que ha seleccionado “Text entry only”. Pulse OK y entonces Finish en la ventana de diseño de preguntas.

Esto proporcionará una ilustración de cómo Maple T.A. proporciona a los instructores la capacidad de comprobar el conocimiento conceptual de sus estudiantes para asegurarse de que ellos comprenden cómo se desarrollan las ecuaciones además de saber resolverlas.

Conclusión

Las herramientas de aprendizaje en línea, como las desarrolladas por Maplesoft, proporcionan a los instructores las capacidades para educar con efectividad a sus estudiantes y comprobar su comprensión. La conveniencia proporcionada por estas soluciones de aprendizaje no niega la habilidad para encontrar con efectividad las necesidades de aprendizaje de los estudiantes. A través de la investigación y una creciente familiaridad con Maple, Maple T.A., y ahora Möbius, los educadores pueden mantener un control sobre los contenidos y la evaluación, a la vez que optimizan completamente las funcionalidades de estas herramientas.