- Detalles
- Categoría: Comsol
- Visto: 4402
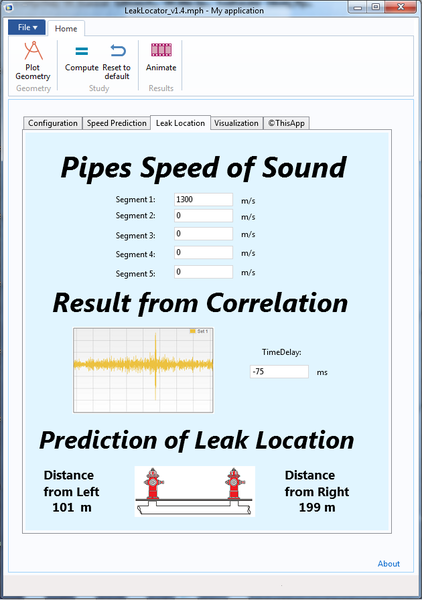
La revista en línea Sensors, publica un interesante artículo sobre una app creada con COMSOL por la empresa Echologics para la detección de fugas en tuberías.
En el artículo, titulado “Multiphysics Analysis Advances Water Main Leak Detection”, Valerio Marra, director de marketing en COMSOL inc. nos explica cómo la empresa Echologics, con sede en Toronto, utiliza el sonido generado por las fugas en las tuberías para detectarlas por medio de sensores acústicos, midiendo el tiempo de propagación de estos sonidos y sus correlaciones.
En la app se aplica un análisis de redes de tuberías, con acoplamientos multifísicos entre la acústica, el flujo y la mecánica estructural.
- Detalles
- Categoría: Maple
- Visto: 6250
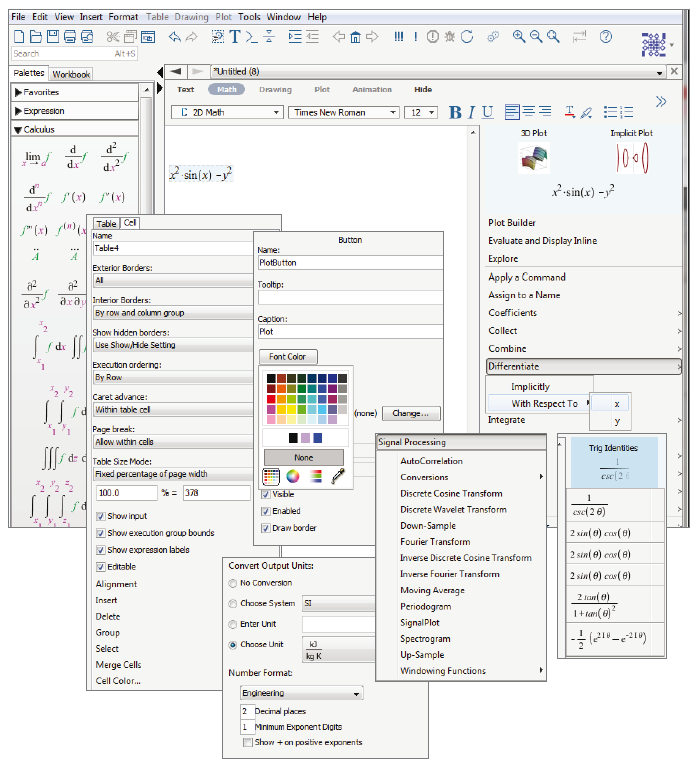
La versión incluye mejoras sustanciales en cómo los usuarios interactúan con Maple
Maplesoft™ acaba de anunciar una nueva versión principal de su producto insignia, Maple™, el programa matemático que facilita enormemente el análisis, exploración, visualización y resolución de problemas matemáticos. Maple 2018 incluye mejoras sustanciales a cómo los clientes interactúan con Maple, proporcionando beneficios significativos a todos los usuarios, sin importar para que usen Maple. La versión también incluye una extensa colección de mejoras en matemática avanzada, visualización, áreas de aplicación especializada, y más, que serán de gran utilidad para matemáticos, educadores, ingenieros y científicos que dependan de estas funcionalidades particulares.
La gente utiliza Maple para realizar muchas tareas diferentes, así que naturalmente el valor de las mejoras en cualquier nueva versión varía para cada usuario. Sin embargo, Maple 2018 no es una versión que cualquier cliente pueda saltarse. Maple 2018 contiene un gran número de mejoras sustanciales en cómo los usuarios interactúan con Maple, lo que significa que todos los clientes verán beneficios inmediatos en esta versión. Estas mejoras incluyen:
- Un Panel Contextual inteligente, que agrupa y mejora algunas de las herramientas Clickable Math™ más potentes, proporcionando un acceso del tipo apuntar y hacer clic a una amplia variedad de operaciones matemáticas y otras herramientas de Maple.
- Mejoras significativas al editor de código de Maple, que hace más fácil y rápida que antes, la escritura, depuración y mantenimiento de código de Maple y las aplicaciones basadas en Maple.
- Integración más profunda de las unidades dentro del motor matemático que simplifica significativamente los cálculos basados en unidades.
- Nuevas opciones para proteger el trabajo de modificaciones o vistas, de forma que los clientes puedan compartir su trabajo mientras mantienen el control de sus contenidos.
Maple 2018 también incluye una amplia variedad de mejoras que profundizan sus capacidades, así como nuevas funcionalidades que amplían su aplicabilidad. Se han realizado mejoras matemáticas en integración, ecuaciones diferenciales ordinarias y parciales, simplificación, teoría de grafos y más. Las nuevas habilidades incluyen geometría computacional, soporte para realizar cálculos que involucren propiedades termoquímicas de especies químicas, generación de hojas prácticas para estudiantes que son evaluadas automáticamente por Maple e interpolación de datos no estructurados.
"Mientras que cada versión de Maple incluye una multitud de mejoras en muchas áreas del producto, la gente utiliza Maple para tareas muy diferentes, y no todos los cambios serán de igual importancia para todos los usuarios. Pero Maple 2018 no es una versión que saltarse," dice el Dr. Laurent Bernardin, Director de Operaciones de Maplesoft. “Con mejoras en tantas de las maneras en que los usuarios interactúan con Maple, ni importa para qué usan Maple, nuestros clientes encontrarán que Maple 2018 hace que el trabajo que hacen en Maple sea much más fácil.”
Para más información sobre las nuevas funcionalidades de Maple 2018 visite la página del producto
- Detalles
- Categoría: Comsol
- Visto: 4214
COMSOL vuelve a ser, junto con Mouse Electronics el patrocinador principal del concurso Create the Future Design Contest. Este concurso fue lanzado en 2002 por los editores de la revista NASA Tech Briefs para ayudar a estimular y premiar la innovación en la ingeniería. Este evento anual ha atraído a más de 14.000 ideas de diseño de productos de ingenieros, empresarios y estudiantes de todo el mundo.
La edición de 2018 ya está abierta y admite propuestas. El concurso reconoce diseños innovadores de productos en siete categorías, con un Gran Premio de 20,000 dólares. No existe coste alguno para participar, y las propuestas pueden ser realizadas por individuos o equipos.
- Detalles
- Categoría: Comsol
- Visto: 5570
Muchos tipos de análisis se benefician de la posibilidad de correr COMSOL Multiphysics® en hardware de computación de alto rendimiento (HPC). Esta es una de las principales razones que están detrás del nodo Cluster Computing, que ayuda a integrar con sencillez el software COMSOL® con cualquier infraestructura HPC, a la vez que se mantiene la conveniencia de la interfaz gráfica de usuario. En esta entrada del blog, Lars Drögemüller nos enseña cómo correr grandes simulaciones de forma remota sobre hardware HPC directamente desde el entorno gráfico de COMSOL Desktop®.
En esta extensa e ilustrativa entrada del blog, Lars nos explica en qué consiste la computación en clúster, cómo añadir un nodo de computación clúster en un modelo sencillo de COMSOL Multiphysics, los ajustes necesarios para el nodo de computación en clúster, cómo se corre un estudio en un clúster, el uso de la funcionalidad de computación en clúster para las simulaciones de COMSOL Multiphysics, la computación clúster con Apps y algunas conclusiones.
- Detalles
- Categoría: Maple T.A.
- Visto: 7724
La Universidad de Birmingham impulsa el aprendizaje utilizando herramientas digitales. Vea ejemplos de nuevos enfoques basados en la investigación y experiencia con la tecnología de Maplesoft.
La tecnología se expande a una rápida velocidad, revolucionando la forma en la que se accede a la información y se distribuye la educación. Esto proporciona a los educadores y estudiantes los beneficios de la conveniencia, facilidad de acceso, mayor interactividad y un uso más económico de los recursos. En el medio de estos beneficios, algunos se preguntan si la dependencia de las herramientas de aprendizaje en línea pone algún obstáculo a la eficiencia o si estas soluciones son capaces de cumplir todas las necesidades de aprendizaje de los estudiantes. Instructores de la Universidad de Birmingham en el Reino Unido han examinado estos asuntos a través de la introducción de herramientas en línea en su arsenal de enseñanza, y han dirigido preguntas y preocupaciones presentadas por educadores externos, para ilustrar cómo herramientas como Maple y Maple T.A. son realmente soluciones de aprendizaje efectivas.
La Universidad de Birmingham implementó Maple T.A. hace varios años, mejorando en gran medida las iniciativas de aprendizaje y enseñanza en la escuela, lo que incluye programas de pregrado y postgrado en asignaturas de ciencias, tecnología, ingeniería y matemáticas (STEM). Maple T.A. es un potente sistema de aprendizaje y evaluación diseñado específicamente para cursos STEM, respaldado por la potencia de cálculo simbólico del motor de Maple. La universidad fue capaz de incrustar el software dentro de su sistema de gestión de aprendizaje (LMS) existente, CANVAS. Al ampliar de forma efectiva su LMS de forma que es capaz de entender las matemáticas, ahora pueden distribuir con mayor extensión y de forma más robusta aprendizajes y evaluaciones de cursos basados en matemáticas.
Además de Maple y Maple T.A., la escuela recientemente adoptó Möbius, el material didáctico STEM completo, en línea, de Maplesoft. Möbius fue introducido en la universidad por el Dr. Tim Jackson para simplificar su curso de ingeniería de primer año, y actualmente existe un grupo de internos en la escuela comprobando las posibilidades de Möbius y trabajando con el profesorado para desarrollar contenido.
El Dr. Jonathan Watkins, un investigador y graduado de doctorado de la Universidad de Birmingham, fue una de las fuerzas creativas detrás de la integración de Maple T.A. con el LMS de la escuela. También fue responsable de la introducción del equipo de creación de contenidos de la escuela. Continúa trabajando con Maplesoft para mejorar el uso de la tecnología de Maplesoft en la escuela y proporcionar a los instructores el conocimiento para optimizar las capacidades de cada herramienta.
Nuevos enfoques
La Universidad de Birmingham adoptó Maple T.A. para mejorar la experiencia de aprendizaje de los estudiantes y optimizar el tiempo de los instructores para trabajar con los estudiantes. A medida que el profesorado se fue haciendo más familiar con las capacidades de Maple T.A., la Universidad decidió utilizar Maple T.A. en toda la universidad, no solo para proporcionar cursos con núcleo matemático. Como resultado, hicieron prioritario desarrollar sus propios contenidos para ajustarse a las necesidades individuales de todos sus estudiantes. Esto también les proporcionó la capacidad de controlar la calidad y cantidad, y asegurar que todos los materiales distribuidos se ajustaban a los altos estándares educaciones de la escuela.
Armados con contenidos personalizado y robusto, el personal introdujo nuevos enfoques a sus estilos de enseñanza y aprendizaje. A continuación se muestran dos ejemplos específicos que detallan cómo la universidad ha utilizado Maple T.A. para involucrar mejor a sus estudiantes y optimizar sus rutas de aprendizaje. El primer ejemplo ilustra cómo la universidad utilizó Maple T.A. para recompensar a los estudiantes por el proceso de llegar a una respuesta, no solo por la respuesta final. Esto anima a los estudiantes a pensar a través del problema y en cada paso para alcanzar la respuesta final. El segundo ejemplo muestra varios métodos introducidos para animar a los estudiantes a pensar más críticamente y desafiarse más para comprender conceptos matemáticos.
Parámetros de evaluación personalizados
Los miembros del grupo de creación de contenidos de Maple T.A. de la Universidad de Birmingham investigaron menearas de aplicar un mayor nivel de juicio humano a sus herramientas de evaluación, para proporcionar a los profesores un mayor control sobre los detalles y la calidad de las entradas que los estudiantes pueden proporcionar, así como la manera en que las pruebas y tareas son evaluadas en Maple T.A. Su equipo de contenidos trabajó con Maple T.A. para implementar maneras para reconocer los esfuerzos de los estudiantes y los procesos de pensamiento a medida que trabajan en la pregunta, más allá de la respuesta final.
Como un problema de ejemplo, los investigadores examinaron el gráfico de la Figura 1 más abajo. El gráfico se generó automáticamente utilizando Maple.
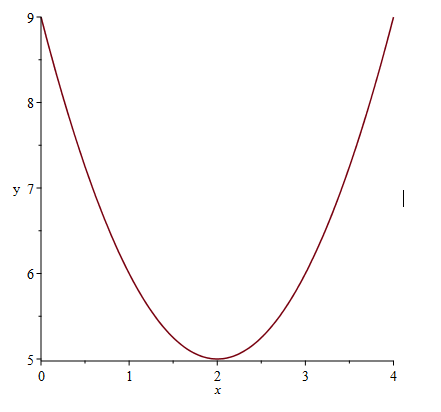
Figura 1. Gráfico generado por Maple
Para este gráfico, la forma de la respuesta puede especificarse en la pregunta como una lista [x, y]. Un estudiante puede identificar el mínimo como [2,5] pero igualmente pueden entrar [2.1, 4.9]. Ambos de estos intentos deben de ser recompensados igual, igual que si estuvieran marcados por una única persona.
Los pasos más abajo ilustran cómo crear esta pregunta en Maple T.A.
PASO 1
PASO 2
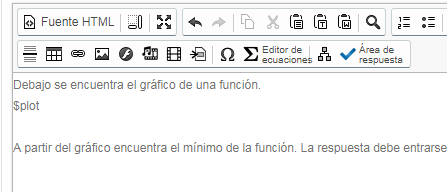
Los creadores de contenidos pueden entrar el texto de la pregunta, como se muestra más abajo. Para el área de respuesta, se escoge Maple-graded y se entra el código de evaluación como sigue:
evalb(abs($TA[1]-$RESPONSE[1]) < $abserr and abs($TA[2]-$RESPONSE[2]) < $abserr)
Se selecciona $TA como la respuesta y se escoge Maple syntax y “Text entry only”.
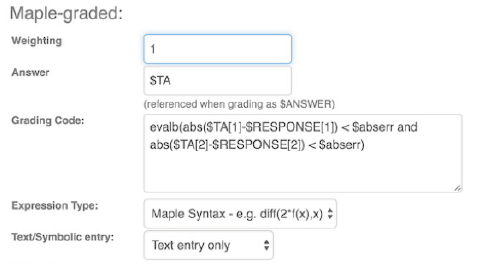
PASO 3
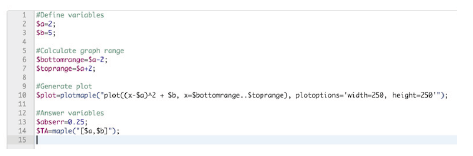
Se entra el algoritmo como sigue:
#Define variables
$a=2;
$b=5;
#Calculate graph range
$bottomrange=$a-2;
Stoprange=$a+2;
#Generate plot
$plot=plotmaple(“plot((x-$a)^2 + $b, x=$bottomrange..$toprange), plotoptions=’width=250, height=250’”);
#Answer variables
$abserr=0.25;
$TA=maple(“[$a,$b]”);
Ahora la pregunta está completada. Esto proporciona una ilustración de cómo los instructores que trabajan con Maple T.A. pueden estructurar las preguntas para que les proporcione un mayor grado de control sobre su evaluación de las respuestas de los estudiantes.
Cálculo de la comprensión conceptual
A medida que los estudiantes progresan en su educación pueden convertirse en adeptos en preparar pruebas y evaluaciones, y resolver los problemas que se les presentan. Sin embargo, la investigación ha mostrado que esto no es un indicador de la comprensión conceptual. En otras palabras, solo porque un estudiante pueda tener el conocimiento para resolver un problema no significa que realmente comprendan el concepto que existe detrás del problema en sí.
Durante el curso de un programa de grado, los estudiantes a menudo se hacen expertos en resolver problemas cuando se les proporciona los conjuntos de ecuaciones que necesitan resolver. Como la mayoría de instructores darán fe, la habilidad que a menudo les falta es la capacidad de producir este conjunto de ecuaciones en primer lugar. Con Maple T.A., es una tarea bastante trivial pedir a un estudiante que entre la solución a un sistema de ecuaciones y tener el sistema de verificación de que lo ha entrado correctamente. El Dr. Watkins encontró que muchos profesores con los que habló querían ser capaces de desafiar a sus alumnos a pensar más allá sobre los conceptos en sí mismo. Querían que sus estudiantes tuvieran la habilidad de proporcionar las ecuaciones gobernantes y las condiciones de contorno para un problema específico.
Maple T.A. permite a los instructores calcular la comprensión conceptual, utilizando su motor matemático único para verificar si los estudiantes son capaces o no de formar el sistema de ecuaciones por ellos mismos, además de resolverlo. Utilizando un flujo de Couette 2D como ejemplo, el Dr. Watkins exploró cómo Maple T.A. podría ser utilizado para configurar una pregunta que abordara estos objetivos. Un flujo de Couette es una configuración de dinámica de fluidos que consiste en el flujo de un líquido viscoso en el espacio entre dos superficies, una de las cuales se mueve tangencialmente en relación a la otra. La Figura 2 se creó utilizando el diseñador de preguntas de Maple T.A., que proporciona una interfaz uniforme para el diseño de preguntas y más flexibilidad sobre la disposición del texto de la pregunta presentada al estudiante.
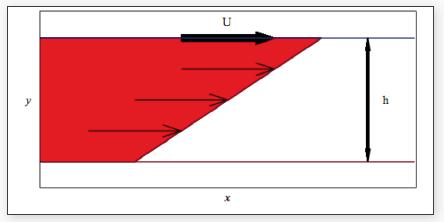
Figura 2. Flujo laminar de un líquido viscoso incompresible entre dos líneas paralelas
Al determinar el sistema de ecuaciones que especifica este sistema, los términos se pueden introducir como una lista separada por comas, seguida por la inserción de un cuadro de respuesta evaluado por Maple. Al utilizar el diseñador de preguntas, las respuestas a menudo son más largas que el ancho del cuadro de respuestas. Una manera de solucionarlo es cambiar el ancho de todas las cajas de entrada de una pregunta utilizando una etiqueta de estilo. Por ejemplo, uno puede hacer clic en el botón “source” del editor y entrar lo siguiente al principio de la pregunta:
<style id=”previewTextHidden” type=”text/css”>
input[type=”text”] {width:300px !important}
</style>
Aprentando “source” otra vez se mostrará el resultado de este cambio. El cuadro de entrada ahora será significativamente más ancho. Después necesitaremos añadir el algoritmo para esta pregunta. La respuesta del profesor para esta pregunta es el sistema de ecuaciones para el flujo de la figura:
$TA=”diff(u(y),y,y) = 0, u(0) = 0, u(h) = U”;
$sol=maple(“dsolve({$TA})”);
Es recomendable que los que desarrollen preguntas establezcan esto en $TA por consistencia entre preguntas. Para comprobar que existe una solución, utilice una llamada de Maple a la función dsolve de Maple, que devolverá la solución al sistema proporcionado de ecuaciones. Apretar refresco después de que el algoritmo realice estas operaciones y verifique la respuesta del instructor.
La parte clave de esta pregunta es el código de evaluación en el cuadro de respuesta evaluada por Maple. Añada el cuadro de respuesta al texto de la cuestión al final del texto que añadimos en el paso anterior. Haga clic en el área Insert Response y escoja el cuadro de respuesta evaluado por Maple en el menú de la izquierda. Para la respuesta, entre la variable $TA que definimos en el algoritmo. Para el código de evaluación, entre:
a:=dsolve({$RESPONSE}): evalb({$sol}={a})
Este código verifica que el sistema de ecuaciones del estudiante produce la misma solución que la del professor. Al preguntar la cuestión de esta manera se permite una respuesta más abierta del estudiante. Para finalizar asegúrese que el tipo de expresión es Maple syntax y que ha seleccionado “Text entry only”. Pulse OK y entonces Finish en la ventana de diseño de preguntas.
Esto proporcionará una ilustración de cómo Maple T.A. proporciona a los instructores la capacidad de comprobar el conocimiento conceptual de sus estudiantes para asegurarse de que ellos comprenden cómo se desarrollan las ecuaciones además de saber resolverlas.
Conclusión
Las herramientas de aprendizaje en línea, como las desarrolladas por Maplesoft, proporcionan a los instructores las capacidades para educar con efectividad a sus estudiantes y comprobar su comprensión. La conveniencia proporcionada por estas soluciones de aprendizaje no niega la habilidad para encontrar con efectividad las necesidades de aprendizaje de los estudiantes. A través de la investigación y una creciente familiaridad con Maple, Maple T.A., y ahora Möbius, los educadores pueden mantener un control sobre los contenidos y la evaluación, a la vez que optimizan completamente las funcionalidades de estas herramientas.
- Detalles
- Categoría: ChemOffice
- Visto: 162212
La estereoquímica es la parte de la química que estudia la distribución espacial de los átomos que componen las moléculas con el fin de conocer la influencia de estos sobre sus propiedades químicas y físicas, así como su reactividad. Proporciona conocimientos para la química en general, ya sea inorgánica, orgánica, biología, fisicoquímica o química de polímeros.
Uno de los casos médicos en los que la estereoquímica jugó una mala pasada es el conocido “desastre de la Talidomida”. En el año 1953 una compañía farmacéutica, Ciba, desarrolló este fármaco sin pensar en los resultados que podría tener. Fue comercializado como sedante y calmante para las náuseas producidas durante los primeros meses de embarazo. Se realizaron estudios en diversos animales de laboratorio para comprobar los efectos secundarios, pero no se encontró ninguno. Más tarde se conoció que la talidomida se había dispensado en dosis tan altas que los fetos de los animales embarazados habían fallecido.
Los resultados habían sido falseados y, por consiguiente, el fármaco salió al mercado con problemas serios en su estructura química que podría desencadenar graves problemas en los pacientes que lo ingirieran. Tras múltiples investigaciones se descubrió que existían dos talidomidas distintas, aunque de igual fórmula molecular, en las cuales cambiaba la disposición de los grupos en un carbono en el espacio, cosa que hasta entonces no se tenía en cuenta. Se trataba, por tanto, de una sola molécula con dos enantiómeros. Están pues (según la nomenclatura actual) la forma R (que producía el efecto sedante que se buscaba) y la S (que producía efectos teratogénicos y producía focomelia). Este descubrimiento produjo que a partir de ese momento se tuviese en cuenta la estereoisomería en moléculas, utilizando el sistema R/S actual.
Es por ello por lo que la estereoquímica es fundamental en la preparación de medicamentos o compuestos destinados a actuar sobre organismos. Por ello, ChemDraw 17 pone a disposición del usuario herramientas tan precisas y completas como:
- Dibujo de enlaces especiales.
- Estereoquímica de proyecciones y representaciones.
- Estequiometría absoluta.
- Estequiometría relativa.
- Creación de enantiómeros: imagen de espejo.
Dibujo de enlaces especiales
ChemDraw nos ofrece una amplia gama de enlaces simples y dobles que podemos utilizar para dibujar con mayor precisión nuestras estructuras químicas.
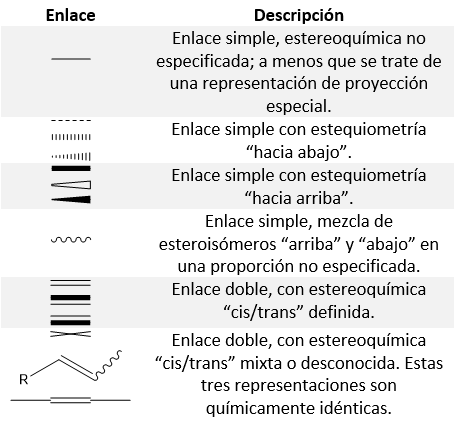
El tipo de enlace que seleccionemos para dibujar nuestra estructura será vital para la obtención de las propiedades adecuadas de la misma. De esta forma, en función de que nuestro compuesto químico presente disposición “cis” o “trans” sus propiedades pueden ser unas u otras debido a las interacciones entre los grupos funcionales en consecuencia del tamaño de los mismos.
Estereoquímica en proyecciones y representaciones
La representación de enlaces simples sin disposición espacial puede suponer varios estereocentros dentro de la misma estructura.
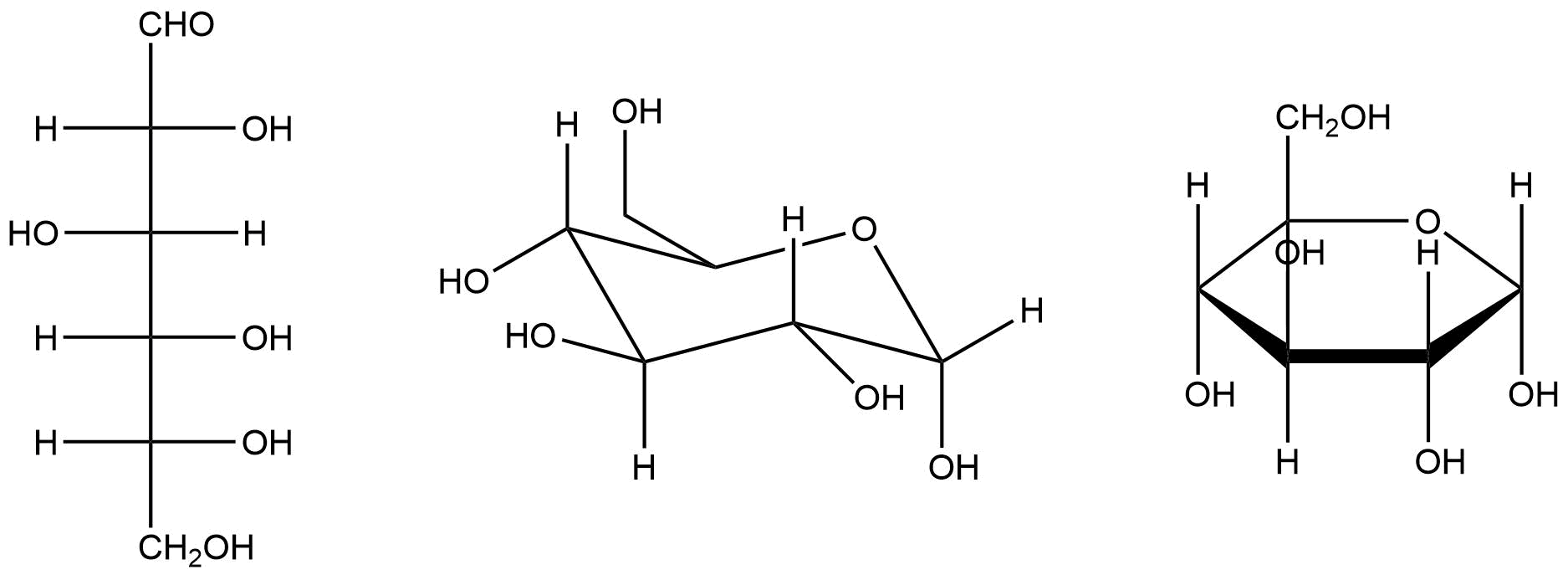
Las tres proyecciones anteriores representan variaciones de glucosa, molécula con múltiples centros quirales. En este caso, debido a las reglas utilizadas en las representaciones utilizadas, no será necesario indicar la orientación de los grupos funcionales con enlaces tipo “cuña” o “hash”. ChemDraw interpreta la estereoquímica de acuerdo con las convenciones establecidas para cada proyección. A continuación, se muestran las tres mismas moléculas especificando la estereoquímica de sus centros quirales, para lo cual hay que seguir los siguientes pasos:
- Selección de la molécula a estudiar.
- “Object” – “Show Stereochemistry”
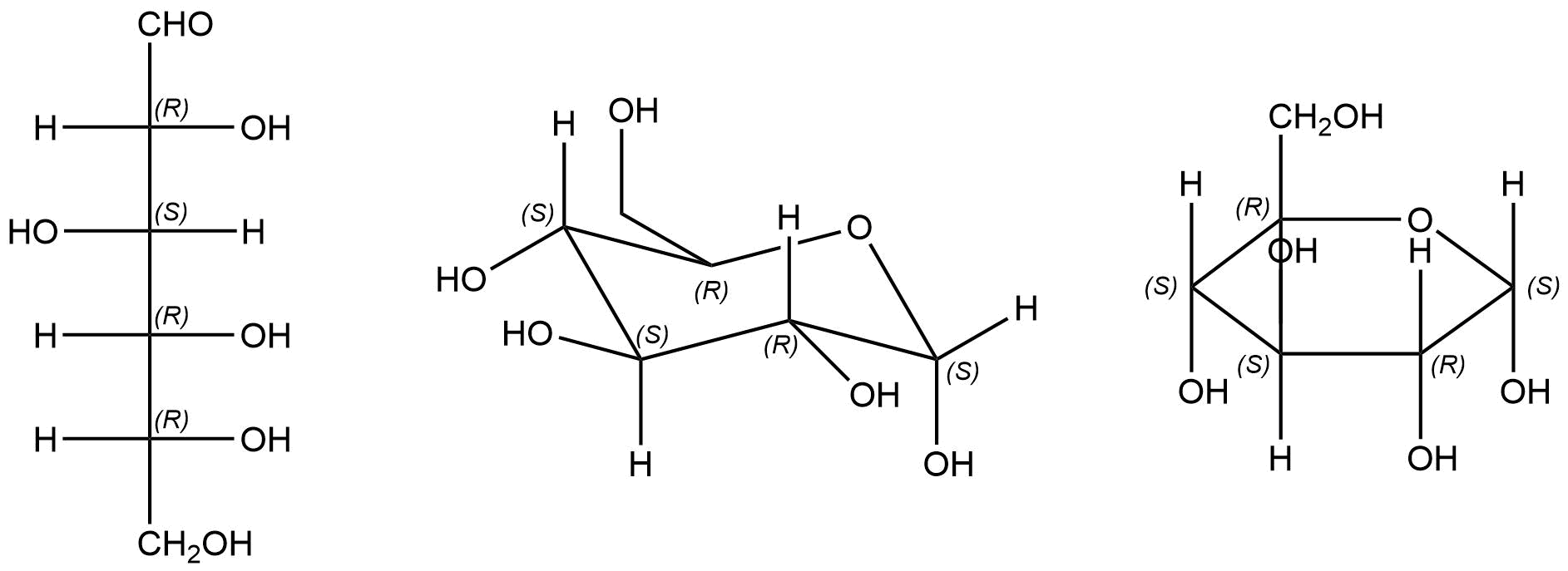
ChemDraw también puede interpretar representaciones mixtas. En la proyección de Haworth de la glucosa (abajo a la izquierda), la forma alfa-glucofuranosa, presenta orientaciones de enlaces muy variadas. A pesar de ello ChemDraw es capaz de identificar la orientación de los grupos funcionales y de mostrar sin ningún tipo de error la estereoquímica del carbono.
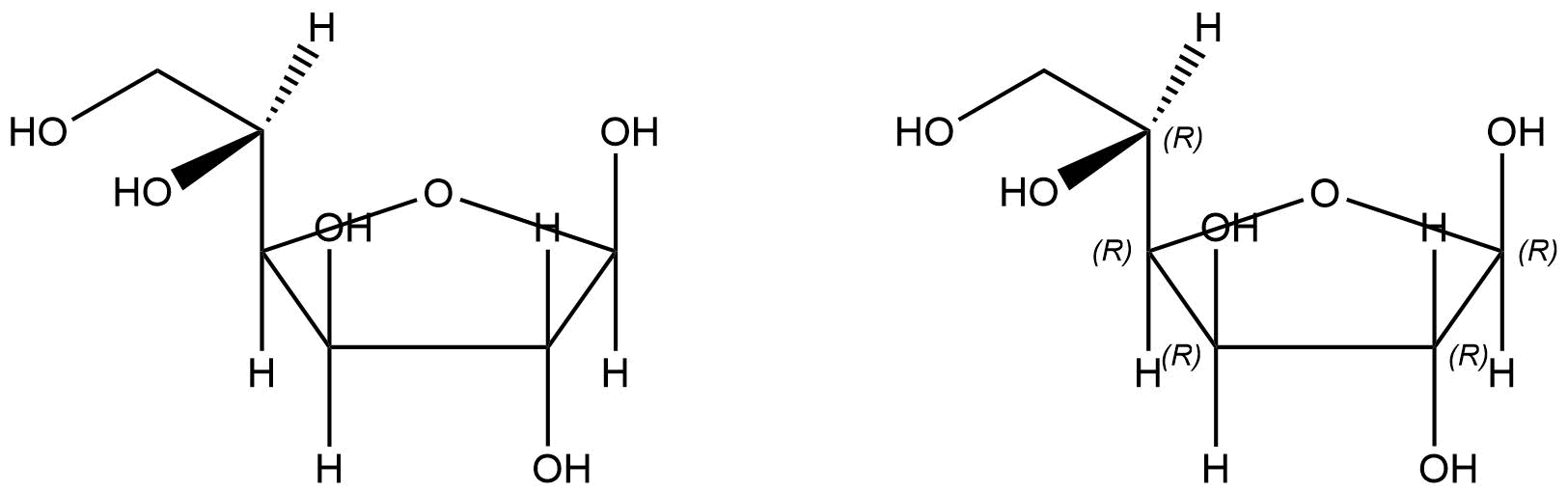
Estereoquímica absoluta
Podemos calcula la estequiometría absoluta de acuerdo con las reglas de prioridad de Cahn-Ingold-Prelog (CIP). Dentro de la opción “Object” – “Show stereochemistry” solo podremos analizar estructuras con geometría tetraédrica o dobles enlaces, como se muestra a continuación.
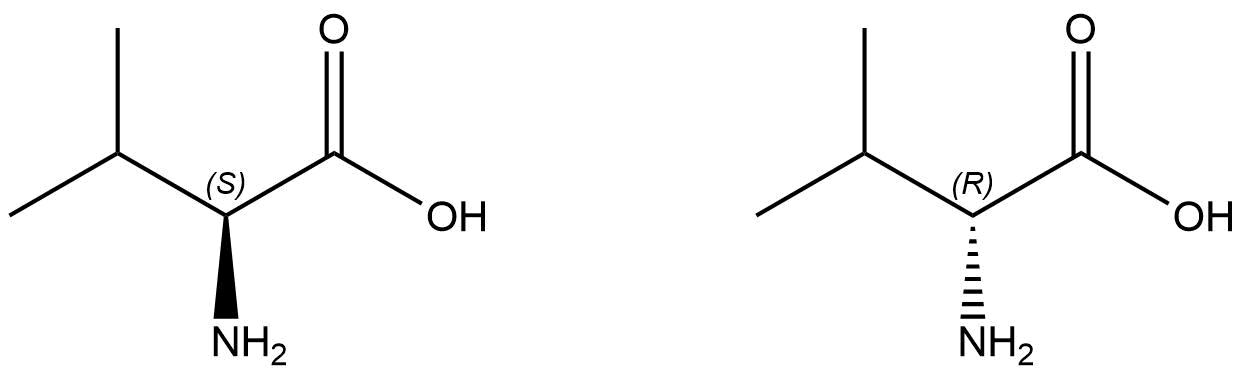
Como podemos ver, en el caso de la valina, la estequiometría que nos aporta sobre el carbono quiral indica que se trata de un centro asimétrico, átomo que ChemDraw es capaz de reconocer a la perfección.
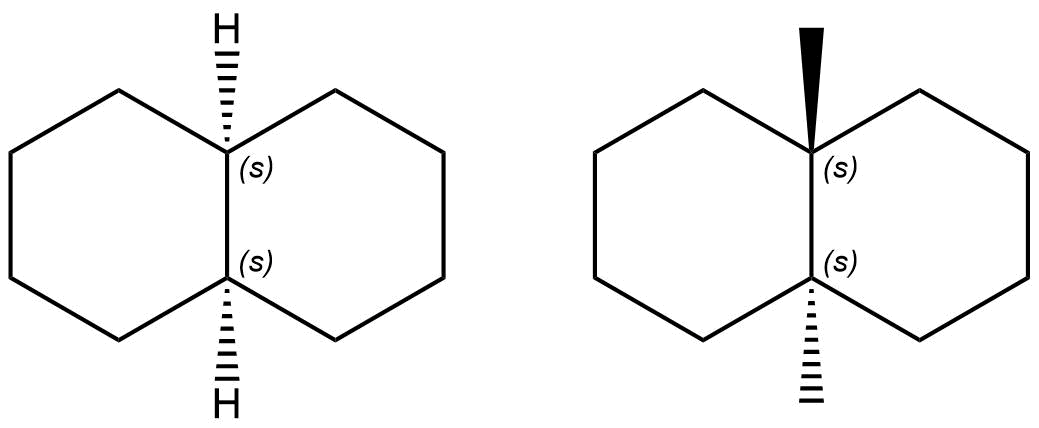
En cambio, para el análisis estereoquímico de la Cis/trans-decalina la información que ChemDraw nos aporta está relacionada con centros pseudoasimétricos (r) y (s).
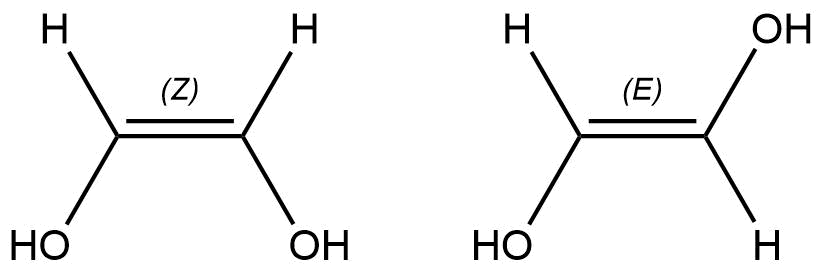
En el caso de estructuras con dobles enlaces, la opción citada al inicio de este apartado nos aporta información sobre la distribución en el espacio de los grupos funcionales asociados al doble enlace (Z) o (E).
Estereoquímica relativa
Los investigadores pueden especificar relaciones entre grupos de estereocentros dentro de la misma molécula. Este tipo de notación aporta más información de lo que los indicadores estequiométricos de ChemDraw anteriores pudiera aportar. A continuación, se muestra un ejemplo de como utilizar esta notación estequiométrica.
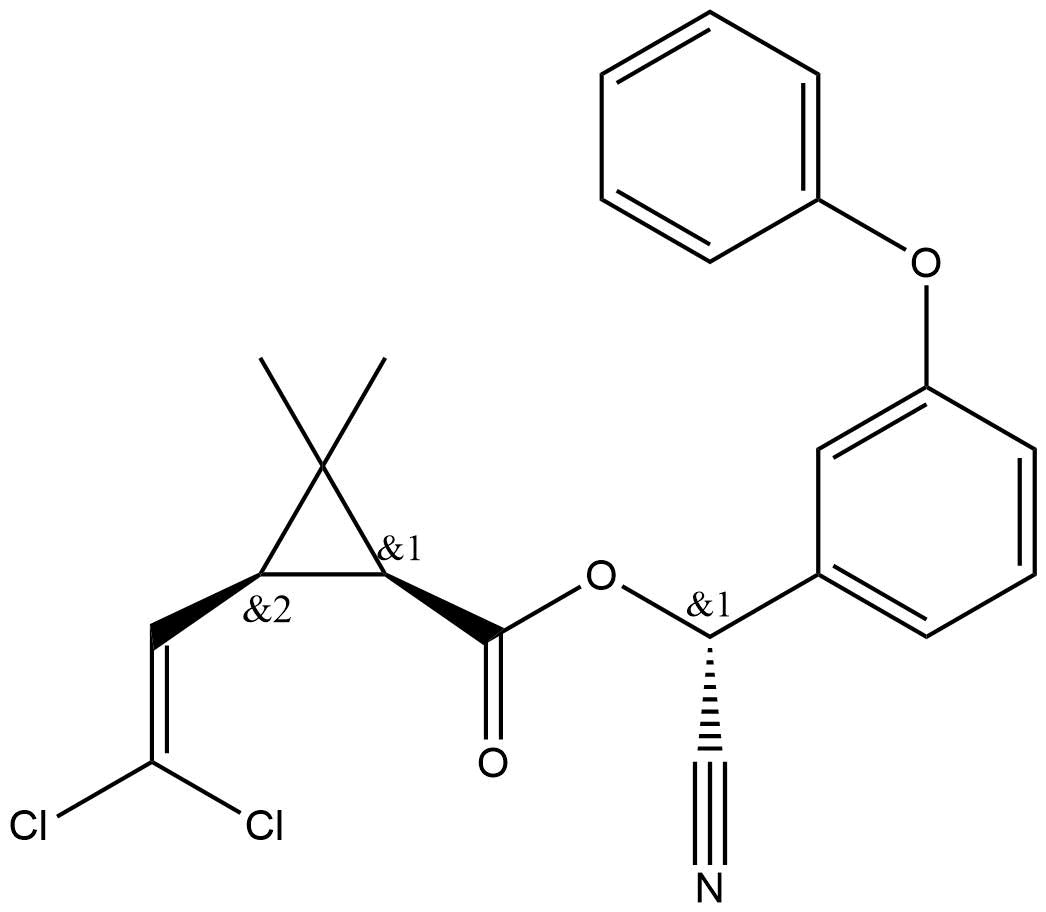
Dos estereocentros tienen designación “&1” debido a su configuración relativa fija: cuando uno es “R”, el otro debe ser “S”. Como resultado, forman un grupo. El tercer estereocentro varía de forma independientemente y se designa como “&2”. Los números de grupo se incrementan automáticamente.
Creación de enantiómeros: imagen de espejo
Los investigadores pueden reflejar estructuras a través de planos perpendiculares en el eje X o Y. De esta forma se pueden representar mezclas racémicas y otros esteroisómeros. También se puede crear una vista del lado reverso de una estructura con estereoquímica definida una vez rotada. Las estructuras giradas no son imágenes especulares, pero a menudo se confunden con imágenes reflejadas.
¿Qué ocurre con las moléculas cuando se rotan? El cambio de orientación de la misma produce un cambio R/S, automáticamente ChemDraw realiza este cambio sin que el usuario tenga que seleccionar ninguna herramienta más.
Conclusiones
La estereoquímica es indispensable para un buen uso de la química. Es inevitable disponer de estos conocimientos para poder aportar la conformación necesaria a nuestros compuestos químicos. Como hemos podido ver, un simple cambio en la orientación de los grupos funcionales puede suponer un gran cambio en las propiedades de un compuesto, convirtiendo nuestra estructura en un compuesto potencialmente peligroso. ChemDraw ofrece herramientas para solucionar estos problemas, ayudando al investigador a plantear las diferentes posibilidades, permitiendo de esta forma un estudio más profundo previo a la síntesis.
- Detalles
- Categoría: Minitab
- Visto: 8140
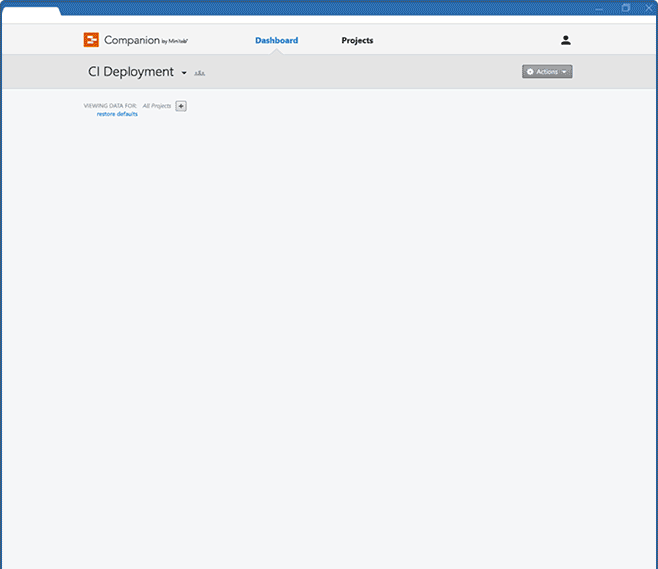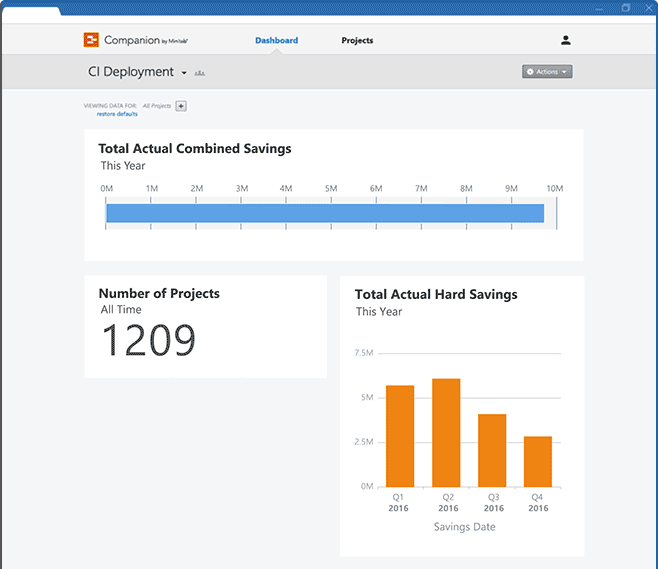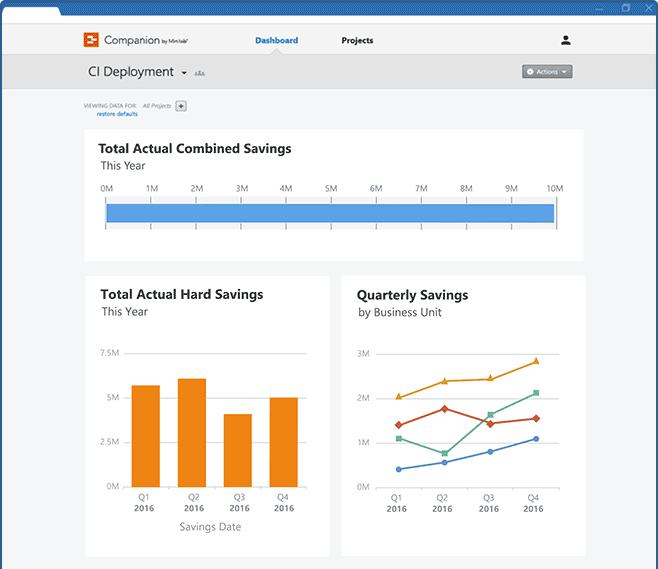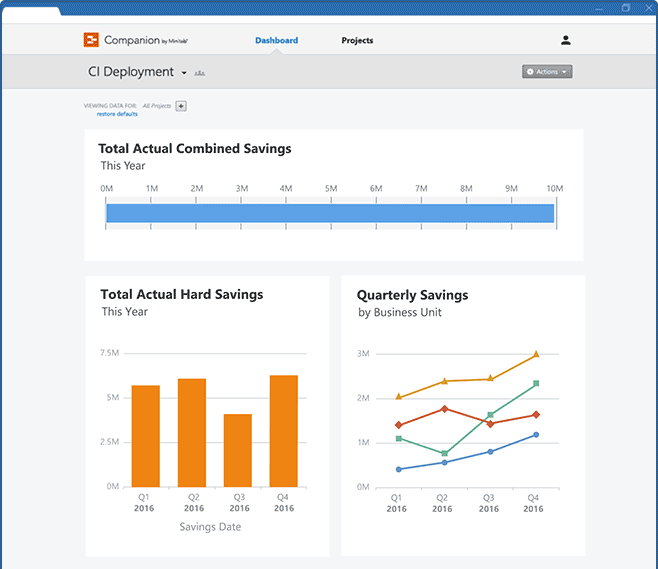
Companion by Minitab® es una extensa plataforma para desarrollar e informar sobre los proyectos de mejora de procesos. Incluye un conjunto de herramientas de escritorio integrado para completar proyectos y un tablero basado en la web que instantáneamente recopila todos los datos del proyecto.
Desde el inicio de cada proyecto, a través de los inormes de las métricas y finanzas clave, Companion permite ver el impacto de los programas demejora con resúmenes automáticos, actualizados al minuto. Companion ayuda a los equipos a completar sus proyectos de forma más rápida y consistente, a la vez que proporciona a todos los participantes la visión necesaria para tomar decisiones críticas para el negocio.
Companion se despliega rápidamente- toda la organización puede estar funcionando en cuestión de días. Los mapas de ruta y las plantillas, fáciles de personalizar, aseguran que los equipos sigan los métodos de la empresa y proporcionen la información necesaria.
Companion es la solción para gestionar, comprender y compartir el impacto de los programas de mejora continua.
Manténgalo unido
 |
Organiza todos los elementos del proyecto en mapas de ruta personalizables (incluyendo DMAIC, Kaizen, QFD, CDOV, PDCA, y Just Do It), todo almacenado en un archivo de proyecto compartible. La aplicación de escritorio incluye mapa de flujo de valor (VPM), simulación Monte Carlo, despliegue de la función de calidad (QFD), tormenta de ideas, FMEA, mapeo de procesos y más de otras 100 herramientas y formularios integrados. Cuando los equipos siguen mapas de ruta estandarizados y utilizan las mismas herramientas se asegura la consistencia entre proyectos. Los datos de los proyectos fluyen sin esfuerzo a una estructura de informes centralizada para mantener a todos los participantes informados. |
Conozca su balance
 |
El tablero de Companion proporciona visibilidad dentro de todo el programa-es fácil calcular el progreso de todos los proyectos, o solo de un subconjunto. Monitorización de los indicadores clave de rendimiento (KPI) necesarios para tomar importantes decisiones de negocio. Búsqueda, apertura y exploración de proyectos para ver actividades detalladas al nivel de proyecto individual. Los informes dinámicos proporcionan a todos en la compañía acceso a la información que se desea compartir. Se puede restringir el acceso a proyectos y datos sensibles a las personas apropiadas. |
Incremento de acceso y reducción de la demanda IT
 |
El almacenamiento centralizado, basado en la web, elimina la necesidad de servidores in-situ y sistemas de respaldo. Puede accederse a companion.minitab.com desde cualquier ordenador conectado a internet, tableta o dispositivo móvil. Los proyectos, plantillas e informes son almacenados con seguridad en la nube. Las copias de respaldo diarias, semanales y mensuales, automáticas, salvaguardan los datos utilizando los últimos métodos. La seguridad del sistema es verificada y comprobada por expertos de terceras partes. |