Bonnie K. Stone

En la Parte 1 de esta serie de entradas en el blog de Minitab, Bonnie escribió sobre cómo la inferencia estadística utiliza datos de una muestra de individuos para llegar a conclusiones sobre toda la población. Esa es una herramienta muy potente, pero cuando se hagan inferencias estadísticas se deben de verificar las suposiciones. La violación de cualquiera de estas suposiciones puede dar lugar a falsos positivos o falsos negativos, invalidando así los resultados.

Los suposiciones respecto a los datos más comunes son: muestras aleatorias, independencia, normalidad, igual varianza, estabilidad, y que el sistema de medición es preciso y exacto.

La última vez se habló de las muestras aleatorias y la independencia estadística. Ahora se considerarán los supuestos de Normalidad e Igualdad de Varianza.

¿Qué es la asunción de la normalidad?

Antes de realizar una prueba estadística, debe averiguarse la distribución de los datos. Si no se hace, hay riesgo de seleccionar una prueba estadística inadecuada. Muchos métodos estadísticos comienzan con el supuesto de que los datos siguen la distribución normal, incluidas las pruebas t de 1 y 2 muestras, la capacidad del proceso, I-MR y ANOVA. Si no se tienen datos distribuidos normalmente, podrá usarse una prueba no paramétrica equivalente basada en la mediana en lugar de la media, o probar la Transformación de Box-Cox o Johnson para transformar los datos no normales en una distribución normal.

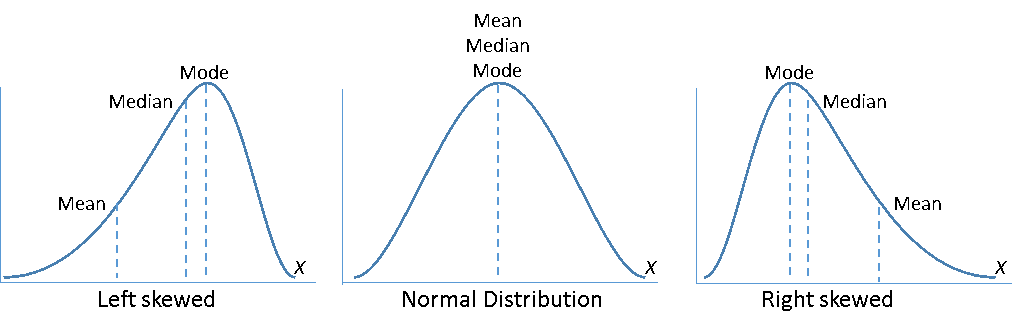
Pero se ha de tener en cuenta que muchas herramientas estadísticas basadas en el supuesto de normalidad no requieren datos distribuidos normalmente si los tamaños de muestra son al menos 15 o 20. Pero si los tamaños muestrales son menores de 15 y los datos no están distribuidos normalmente, el p valor puede ser inexacto y deberán interpretarse los resultados con precaución.

Hay varios métodos para determinar la normalidad en Minitab, y en este artículo veremos dos de las herramientas: la Prueba de Normalidad y el Resumen Gráfico.

La prueba de normalidad de Minitab generará un gráfico de probabilidad y realizará una prueba de hipótesis de una muestra para determinar si la población de la que se extrae la muestra no es normal. La hipótesis nula establece que la población es normal. La hipótesis alternativa establece que la población no es normal.

Seleccione Estadísticas> Estadísticas básicas> Prueba de normalidad

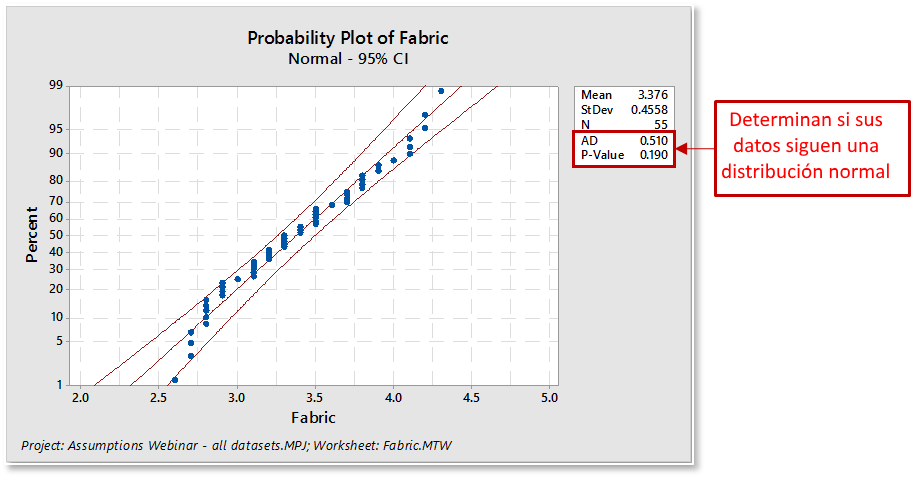
Al evaluar el ajuste de la distribución para una prueba de normalidad:

• Los puntos trazados formarán aproximadamente una línea recta. Alguna desviación de la línea recta en las colas puede estar bien siempre y cuando se mantenga dentro de los límites de confianza.
• Los puntos trazados deben caer cerca de la línea de distribución ajustada y pasar la prueba del "lápiz grueso". Imagine un "lápiz grueso" que se encuentra en la parte superior de la línea ajustada: si cubre todos los puntos de datos de la gráfica, es probable que los datos sean normales.
• La estadística de Anderson-Darling asociada será pequeña.
• El p valor asociado será mayor que el nivel α elegido (los niveles comúnmente elegidos para α incluyen 0.05 y 0.10).

La estadística de Anderson-Darling es una medida de lo lejos que caen los puntos del gráfico de la línea ajustada en una gráfica de probabilidad. La estadística es una distancia cuadrada ponderada desde los puntos del gráfico hasta la línea ajustada con pesos más grandes en las colas de la distribución. Para un conjunto de datos y una distribución específicos, cuanto mejor se ajuste la distribución a los datos, más pequeña será esta estadística.

Las estadísticas descriptivas de Minitab con el resumen gráfico generarán una buena visualización de sus datos y calcularán el valor de Anderson-Darling & p-valor. El resumen gráfico muestra cuatro gráficos: histograma de datos con una curva normal superpuesta, diagrama de caja e intervalos de confianza del 95% para la media y la mediana.

Seleccione Estadísticas> Estadísticas básicas> Resumen gráfico

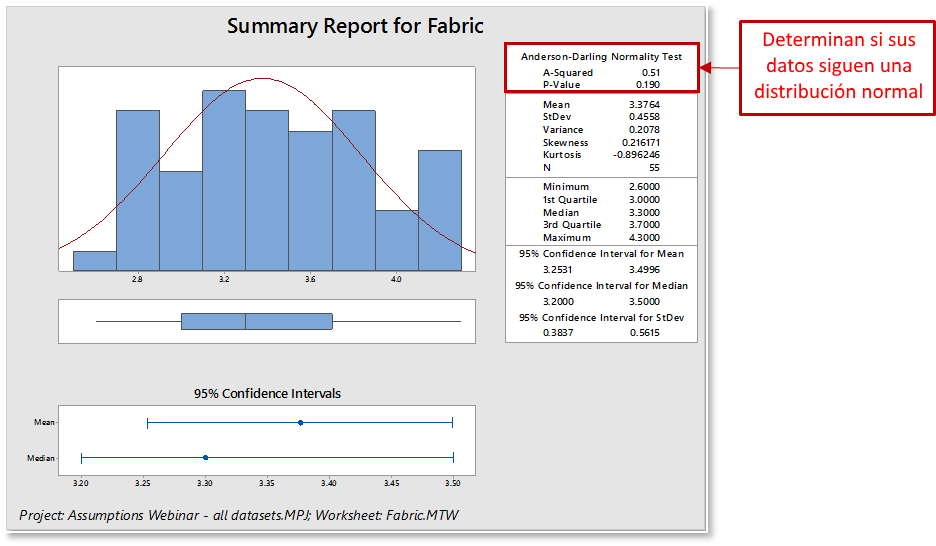
Al interpretar un informe de resumen gráfico para la normalidad:

• Los datos se mostrarán como un histograma. Busque la forma en que se distribuyen sus datos (normal o sesgada), cómo se distribuyen los datos en el gráfico y si hay valores atípicos.
• La estadística asociada de Anderson-Darling será pequeña.
• El valor p asociado será mayor que el nivel α elegido (los niveles comúnmente elegidos para α incluyen 0.05 y 0.10).

Para algunos procesos, como los datos de tiempo y ciclo, los datos nunca se distribuirán normalmente. Los datos no normales están bien para algunos métodos estadísticos, pero asegúrese de que sus datos cumplan con los requisitos para su análisis particular.

¿Qué es la asunción de igual varianza?

En términos simples, la varianza se refiere al ensanchamiento o dispersión de los datos. Las pruebas estadísticas, como el análisis de varianza (ANOVA), suponen que, aunque diferentes muestras pueden provenir de poblaciones con diferentes medias, tienen la misma varianza. Varianzas iguales (homoscedasticidad) es cuando las varianzas son aproximadamente iguales en todas las muestras. Las varianzas desiguales (heterocedasticidad) pueden afectar a la tasa de error de Tipo I y llevar a falsos positivos. Si se están comparando dos o más medias de muestra, como en la prueba t de 2 muestras y ANOVA, una varianza significativamente diferente podría ocultar las diferencias entre las medias y llevar a conclusiones incorrectas.

Minitab ofrece varios métodos para probar la igualdad de varianzas. Se puede consultar la Ayuda de Minitab para decidir qué método usar de acuerdo con el tipo de datos que se tienen. También es posible utilizar el Asistente de Minitab para verificar esta suposición. (Consejo: cuando se use el Asistente, haciendo clic en "más" se pueden ver consejos de recopilación de datos e información importante sobre cómo Minitab calcula los resultados).

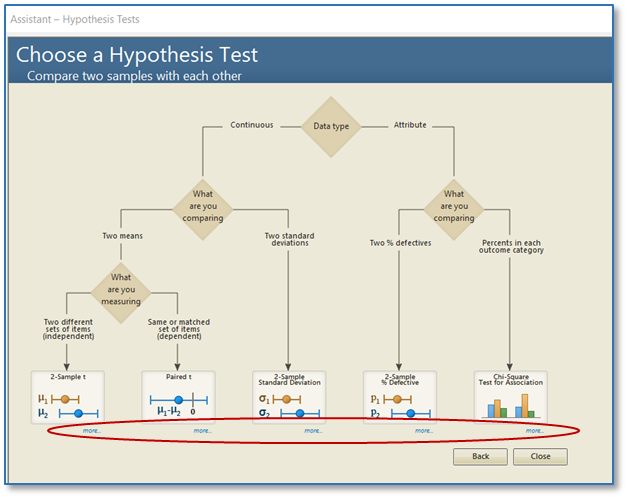
Después de realizar el análisis, verifique el Informe de diagnóstico para la interpretación de la prueba y la Tarjeta de informe para las alertas de puntos de datos inusuales o suposiciones que no se cumplieron. (Consejo: Al realizar la prueba t de 2 muestras y ANOVA, el Asistente adopta un enfoque más conservador y utiliza cálculos que no dependen de la suposición de la misma varianza).

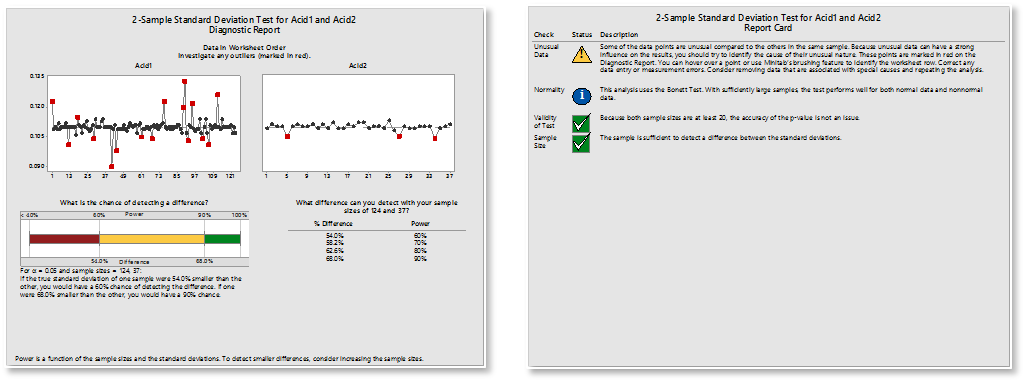
La verdadera razón por la que se necesitan verificar las suposiciones

Se dedica mucho tiempo y esfuerzo a recopilar y analizar datos. Después de todo el trabajo que se ha puesto en el análisis, es deseable poder llegar a conclusiones correctas. Algunos análisis son robustos a los alejamientos de estas suposiciones, ¡pero tome la ruta segura y verifique! ¡Se quiere estar seguro de poder decir si las diferencias observadas entre las muestras de datos se deben simplemente al azar, o si las poblaciones son realmente diferentes!

Es fácil colocar el carro antes que el caballo y simplemente sumergirse en la recopilación y análisis de datos, pero es mucho más inteligente tomarse el tiempo para comprender qué suposiciones de datos se aplican a las pruebas estadísticas que se usarán y planificar en consecuencia.

En la próxima publicación se revisarán las suposiciones comunes sobre la estabilidad y el sistema de medición.