- Detalles
- Categoría: Minitab
- Visto: 4517
Cuando se habla de Big Data todo el mundo entiende que se hace referencia a conjuntos de datos enormes, tanto estructurados como no estructurados, capturados en multitud de ambientes y que requieren de técnicas de procesamiento de datos especiales para poder extraer la información valiosa que pueden contener.
No todas las aplicaciones informáticas están preparadas para realizar este tipo de procesado tanto por el hecho de tener que manejar mucha información como por la necesidad de disponer de herramientas específicas para encontrar patrones, desechar valores sin efecto, visualizarlos adecuadamente, etc.
El interés creciente por manejar estas cantidades inmensas de datos viene por la posibilidad cada vez más fácil de captarlos y después almacenarlos, que además ofrece la posibilidad de realizar estudios estadísticos y obtener modelos predictivos, que luego pueden ser utilizados en ámbitos tan variados como el análisis de negocios, estudios publicitarios, análisis de enfermedades infecciosas, espionaje, seguimiento de la población o en la lucha contra el crimen organizado. Además, el límite de procesamiento ha ido creciendo a lo largo de los años y parece que ese crecimiento va a ser imparable, como mínimo durante las próximas décadas.
Pero es obvio que lo importante no es capturar los datos y almacenarlos. Los datos por si solos no aportan nada. Lo verdaderamente importante es tener la capacidad de saber interpretarlos y para ellos es necesario disponer de una herramienta de análisis como Minitab, que sea capaz de explotar el valor de esos datos.
Atienda al webinar del próximo 25 de septiembre, ofrecido por Addlink Software Científico, titulado “Minitab como herramienta para explotar el VALOR de los DATOS” y conocerá cómo interaccionar con Minitab para obtener diferentes tipos de resultados según el reto que se persigue. Entre otros elementos se presentarán tipos de métricas, estadística descriptiva para resumir, visualizaciones y el valor de cada una, herramientas para predecir, herramientas para experimentar y extracción de resultados para comunicar.
- Detalles
- Categoría: Twinn Witness
- Visto: 10145
Lanner ha trabajado intensamente para mejorar la estabilidad del núcleo y la velocidad de ejecución de WITNESS Horizon en esta última versión. El software también se ha mejorado para soportar Ford en una parte del Proyecto financiada por The Digital Engineering & Test Centre (DETC), incrementando en gran medida la eficiencia (y reduciendo el ciclo de principio a fin) de ejecución de los proyectos de simulación. Ford presentó su trabajo en la reciente Conferencia sobre Simulación Predictiva.
Se ha actualizado el informe de uso de números aleatorios (Random Number Usage) para indicar si los flujos de datos han sido muestreados suficientemente para proporcionar una cobertura fiable del rango aleatorio. Esto ayudará a determinar si un escenario ha estado corriendo suficientemente para obtener resultados fiables.
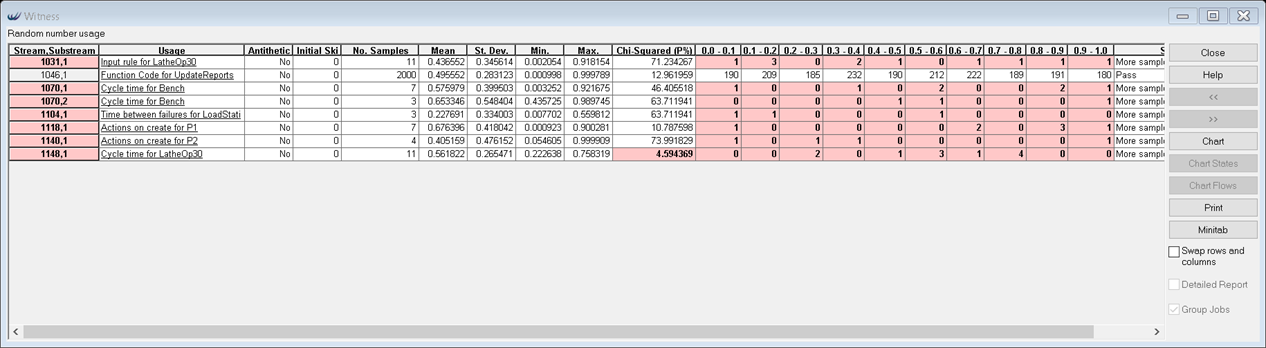
Se han comprobado algunas condiciones de uso para cada flujo de datos aleatorioa que es muestreada y si falla el flujo/subflujo es destacado en el informe con un mensaje de advertencia. Cada flujo/subflujo se comprueba según tres criterios:
- Cada celda 0.1 del rango de muestreo entre 0 y 1 debe tener al menos una entrada – esto es consistente independientemente de qué distribución sea referenciada con el valor muestreado
- No más de 2 celdas de las 10 posibles puede tener menos de 5 entradas
- Las 10 celdas deben aproximarse a una dispersion Uniforme, calculada mediante un test Chi-Cuadrado y verificando que el P valor es mayor que 5%

También se ha mejorado la velocidad de ejecución para modelos con un gran número de elementos, y se han expuesto propiedades y métodos adicionales del modelo a través del API de WITNESS.
En esta versión se han incluido un gran número de soluciones a problemas del software, con un enfoque en los errores de alta prioridad como caídas e inconsistencias de funcionalidad. Esto incluye mejoras a la consistencia de movimientos de partes y trabajadores en caminos y pseudo-caminos, uso de memoria en grandes redes de caminos y numerosas soluciones a problemas que aparecían cuando se coincidían extrañas combinaciones de circunstancias.
- Detalles
- Categoría: Comsol
- Visto: 5458
En esta nueva entrada del blog de COMSOL, Temesgen Kindo complementa la serie de entradas anterior donde se discutían las limitaciones de igualdad en problemas variacionales, mostrando cómo implementar restricciones de desigualdad al usar modelos basados en ecuaciones en COMSOL Multiphysics®.
¿Cómo se encuentra la distancia terrestre más corta entre dos puntos a través de un lago? Este tipo de obstáculos y límites en las soluciones a menudo se llaman restricciones de desigualdad. Los requisitos para obtener gaps no negativos entre objetos en mecánica de contactos, las concentraciones de especies en química y la población en ecología son algunos ejemplos de restricciones de desigualdad.
- Detalles
- Categoría: MapleSim
- Visto: 7982
El modelado de baterías ha recibido un significativo y creciente interés últimamente debido a la aceleración en la adopción de dispositivos electrónicos portátiles, así como el éxito de las industrias de vehículos eléctricos e híbridos (EV/HEV). Estas dos industrias comparten un objetivo común: desarrollar una nueva generación de baterías que permitan dispositivos que funcionen más tiempo, a la vez que trabajan en un rango que maximiza la vida operativa de la batería. En ambos casos, es vital un modelado de la batería preciso y eficiente que ayude a maximizar el rendimiento del dispositivo y su batería. Este artículo técnico delineará cómo MapleSim puede ayudar a hacerlo realidad.
Destacados:
- Vea cómo la Librería de Baterías de MapleSim puede ser utilizada para crar modelos eficientes de alta fidelidad de sistemas de almacenamiento de energía.
- Aprenda como crear modelos de baterías utilizando tanto aproximaciones electroquímicas como de circuitos equivalentes.
- Comprenda las manera de particularizar modelos a sus propias necesidades y modelar los componente eléctricos, químicos y térmicos del sistema de batería.
En este artículo, se presentarán los pasos efectivos y sistemáticos del modelado matemático de modelos de baterías de alta fidelidad para simular sistemas de almacenamiento de energía (ESS). En el artículo se discutirán dos aproximaciones del modelo de batería:
- La aproximación de circuito eléctrico equivalente
- La aproximación electroquímica
Los modelos de batería tratados en este artículo han sido desarrollados basándose en la especificación 3.2.2 de la Librería estándar de Modelica y comercializada como parte de la Battery Library de MapleSim®.
- Detalles
- Categoría: NAG
- Visto: 8662
Numerical Algorithms Group (NAG), expertos en algoritmos, software y HPC han anunciado la reingeniería de su buque insignia NAG Library para Python. La última versión de NAG Library for Python trae nuevos contenidos algorítmicos en el área de optimización matemática. Todo el contenido de la NAG Library funciona perfectamente con los tipos de datos NumPy.
La reingeniería de la NAG Library proporciona a los desarrolladores de Python muchas mejoras a la usabilidad permitiendo el desarrollo más rápido de aplicaciones incluyendo, documentación de rutinas autocontenida, seguridad de hilos, ejemplos curados demostrando algorítmica y funcionalidad importante relacionada con Python, y soporte para llamadas a Python nativo y equivalentes a rutinas en lenguaje C proporcionando una ruta unificada desde el prototipo en Python para distribuir como código compilado.
Además de la NAG Library for Python, hay dos nuevos algoritmos de optimización NAG: Optimización libre de derivativos para la adaptación de datos y Método de punto interior para problemas de programación lineal a gran escala que amplían aún más el número de algoritmos matemáticos y estadísticos disponibles en la NAG Library.
La optimización libre de derivadas para el solucionador de datos fue desarrollado en colaboración con el Centro de Formación Doctoral en Modelado Matemático con Enfoque Industrial (InFoMM) en la Universidad de Oxford. Calibrar los parámetros de modelos numéricos complejos para que se ajusten a las observaciones del mundo real es uno de los problemas más comunes que se encuentran en muchas aplicaciones, como finanzas, simulaciones multifísicas e ingeniería. No es fácil, ni siquiera posible, evaluar derivados de funciones que aparecen en el modelo de optimización y, por lo tanto, muchos enfoques bien establecidos en optimización matemática pueden no ser satisfactorios. Pasar a un régimen libre de derivadas presenta nuevos enfoques para aproximar la solución sin calcular o estimar los derivados. NAG agregó su primer solucionador libre de derivadas a la NAG Library hace aproximadamente cinco años. Desde entonces, este campo ha atraído una gran atención académica, lo que ha dado lugar a numerosos avances. El nuevo solucionador de optimización libre de derivadas puede explotar con eficacia la estructura de los problemas de calibración y se cree que es el primer solucionador comercial de este tipo disponible públicamente en el mundo.
La segunda rutina de optimización es un método de punto interior para problemas de programación lineal a gran escala basado en un paquete de álgebra lineal dispersa muy eficiente e implementa dos variantes de métodos de punto interior: los métodos Primal-Dual y Self-Dual. El Primal-Dual por lo general ofrece la convergencia más rápida y es el solucionador de elección. Ambas implementaciones deberían presentar aceleraciones significativas para problemas a gran escala en comparación con los actuales solucionadores de LP / QP en la Biblioteca. La programación lineal es popular en las finanzas y la logística, en particular la optimización de los procesos de planificación, producción y transporte, pero también se presta a muchos otros campos e industrias.
Un equipo de NAG estará disponible en JupyterCon, la conferencia oficial de Jupyter; una aplicación web de código abierto que le permite crear y compartir documentos que contienen códigos, ecuaciones, visualizaciones y textos narrativos en vivo; y demostrará cómo los algoritmos de la NAG Library pueden brindar múltiples beneficios a sus usuarios.
La NAG Library for Phyton de 64 bits está disponible para Linux, Apple Mac OS y Microsoft Windows y es compatible con Python 2.7, 3.5 y 3.6.
- Detalles
- Categoría: Comsol
- Visto: 9183
Les presentamos la serie de entradas escritas por Temesgen Kindo, en el blog de COMSOL, dedicadas a la simulación y resolución de problemas variacionales con COMSOL Multiphysics
Temesgen nos pregunta ¿qué tienen en común las películas jabonosas, los cables de las catenarias y los haces de luz? Se comportan de forma que minimizan ciertos valores. Este tipo de problemas son frecuentes en los campos de las ciencias y la ingeniería como en biología, economía, teoría de la elasticidad, ciencia de materiales y procesado de imagen. Se pueden simular muchos de estos problemas utilizando las interfaces físicas incluidas en el software COMSOL Multiphysics®, pero en esta serie de entradas del blog nos mostrarán cómo resolver problemas variacionales utilizando las funcionalidades del modelado basado en ecuaciones.
Parte 1: Introduction to Modeling Soap Films and other variational problems
En esta parte se muestra cómo resolver problemas variacionales con restricciones sencillas utilizando la interfaz Weak Form PDE. Esta interfaz viene con la propia instalación de COMSOL Multiphysics. Puede aprender más sobre la forma débil en la siguiente entrada del blog.
En las siguientes entradas se muestra cómo añadir restricciones más sofisticadas, como restricciones de punto, distribuidas e integrales. La serie concluirá generalizando a dimensiones espaciales superiores, derivadas de mayor orden y campos múltiples.
Parte 2: Specifying Boundary Conditions and Constraints in Variational Problems
En este caso se muestran condiciones de contorno y restricciones más generales. También se muestra cómo implementar esas condicines de contorno y restricciones en COMSOL® utilizando el mismo problema variacional de la Parte 1: (la película jabonosa) — y la misma cantidad de matemáticas. Se procede con restricciones más sofisticadas y se utilizan multiplicadores de Lagrange multipliers para configurar problemas equivalentes sin restricciones.
Part 3: Methods for Dealing with Numerical Issues in Constraint Enforcement
En esta parte se hace enfoque especial en los aspectos numéricos de la aplicación de las restricciones. El método de los multiplicadores de Lagrange es teóricamente exacto, sin embargo su uso en soluciones numéricas tiene algunas implicaciones. Se verán estas implicaciones y se mostrarán dos estrategias de mitigación: los métodos Lagrangiano aumentado y de penalización (optimización).
El método de multiplicadores de Lagrange funciona exactamente ... cuando funciona. Sin embargo es más sensible a los estimadores iniciales de la solución y puede convertirse en un problema potencialmente definido indefinido, necesitando el uso de resolvedores directos. Los métodos Lagrangiano aumentado y de penalización superan estos retos como intercambio para algunas violaciones de las restricciones.
Se desea forzar las restricciones exactamente, pero en problemas con inconsistencias o demasiadas restricciones se puede desear forzar las restricciones inexactamente para obtener alguna solución aproximada. En próximas entradas del blogs se discuitrán las restricciones de desigualdad. El método de multiplicadores de Lagrange viene con una desventaja extra para restricciones de desigualdad. Permanezca atento al blog de COMSOL.
Es complicado hacer predicciones, especialmente sobre el futuro (incluso con aprendizaje automático)
- Detalles
- Categoría: Minitab
- Visto: 5670
por Bill Kahn, vicepresidente senior, ejecutivo de modelado de riesgos - Bank of America
Bill Kahn dirige el grupo de modelado estadístico para banca de consumo en Bank of America. Su equipo construye cientos de modelos usando una amplia gama de técnicas estadísticas y de aprendizaje automático. Estos modelos ayudan a garantizar la estabilidad financiera a individuos, empresas y comunidades en todo el país. En las últimas décadas, Bill ha dirigido grupos de estadísticos en varias firmas de servicios financieros, consultoría y fabricación de los Fortune 500. Tiene una licenciatura en física y un master en estadística por la Universidad de Berkeley y su doctorado en estadística de la Universidad de Yale.
Minitab le pidió a Bill que compartiera sus ideas sobre el aprendizaje automático (Machine Learning - ML) como "una base para la acción" en el mundo de los negocios.
Algoritmos de Machine Learning (ML)
En esencia, todos los algoritmos de ML siguen el mismo proceso en dos partes. En primer lugar, una secuencia de funciones crecientemente complejas se ajusta a una parte de los datos (el conjunto de datos de entrenamiento). Luego, cada modelo en la secuencia se evalúa sobre lo bien que se ajusta sobre los datos que se extendieron (el conjunto de retención). Se selecciona el modelo con el mejor ajuste en el conjunto de retención. Existen numerosas variaciones en estos pasos, incluyendo la secuencia explorada, cómo se encuentra cada ajuste, la definición de un buen ajuste y qué selección de aleatoriedad se ha seleccionado. Y resulta que, con un par de modestas precauciones, esta secuencia simple normalmente produce buenos resultados en las predicciones de la muestra.
Las dos precauciones modestas
Primero, necesitamos usar la función de pérdidas correcta para ajustar y evaluar los modelos. Si la función de pérdida no se especifica adecuadamente, todos los algoritmos de aprendizaje automático pueden producir una salida tonta -como clasificar a todos en el grupo predominante y, por lo tanto, fallando al hacer predicciones útiles. Necesitamos usar nuestra experiencia para seleccionar una función de pérdidas con relevancia empresarial, científica o de ingeniería.
En segundo lugar, como cada algoritmo tiene hiperparámetros (parámetros que no pueden establecerse en términos puramente conceptuales), debemos explorar un rango lo suficientemente amplio para garantizar que no estamos utilizando un conjunto de valores malísimo, lo que llevaría a predicciones inaceptablemente débiles.
Prediciendo el futuro
Sin embargo, aunque el aprendizaje automático produzca buenos resultados dentro de las predicciones de la muestra, eso no es lo que necesitamos. Necesitamos buenas predicciones fuera de la muestra. Este salto, de la experiencia pasada al comportamiento futuro, es grande y requiere consideraciones adicionales impulsadas por principios estadísticos básicos. Estas consideraciones incluyen: seleccionar el problema correcto, seleccionar variables dependientes significativas, llamar al sesgo de datos subyacente, comprender la jerarquía y la dependencia entre las observaciones, y construir la secuencia correcta de modelos. Ninguno de estos requisitos es exclusivo de ML; todos son esenciales para que cualquier análisis estadístico sea confiable.
Y finalmente, lo mejor que cualquier modelo puede hacer es extraer la información que realmente está en los datos. Para tener valor, en primer lugar, debe haber información en los datos. Para garantizar que nuestros datos tengan información valiosa, el diseño experimental importa en los modelos de ML, así como también para cualquier otro modelo predictivo. Una vez que uno ha ejecutado un diseño bien estructurado, ahora puede construir un modelo ML y puntuar cada observación para cada combinación posible de variables controlables. Aprendemos la mejor manera de establecer cada entrada controlable (por ejemplo, punto de precio o canal de comercialización o temperatura o velocidad) para producir el mejor resultado para cada entrada.
Este enfoque aprovecha al máximo lo que sabemos, pero tiene una desventaja significativa para cualquier sistema cuyo verdadero estado evolucione. La mejor configuración de los factores de control se deriva cuando el entorno exógeno se desplaza (como la evolución de la calidad de la materia prima, las compensaciones del consumidor o la respuesta de la competencia). Si siempre hacemos una única asignación óptima para cualquier entrada particular, confundiremos lo que observamos con lo que hacemos. Esto hace que construir un modelo nuevo y mejorado sea imposible. Los diseños experimentales más nuevos, como el muestreo de Thompson, resuelven este problema al desafiar continuamente nuestras creencias actuales. Estos diseños nos permiten lograr un equilibrio óptimo entre hacer dinero ahora y aprender lo que necesitamos para poder ganar dinero en el futuro también.
ML es una poderosa adición al conjunto de herramientas del profesional. Con algunas precauciones básicas, que nos permiten evitar lo tonto y lo horrible, y en combinación con el conjunto completo de habilidades estadísticas clásicas, ML nos ayuda a ser estadísticos cada vez mejores.





