- Detalles
- Categoría: Minitab
- Visto: 5836
Si realmente se desea aprovechar el análisis predictivo para resolver los desafíos cotidianos, se debe de aumentar el poder analítico de los analizadores con los mejores algoritmos de aprendizaje automático más precisos de su clase. Estos proporcionan una visión más profunda de los datos. Además de proporcionar métodos estadísticos tradicionales, Minitab ha hecho que los métodos más avanzados, como los métodos basados en árboles, sean más accesibles para todos.
Lleve sus capacidades de regresión fuera de este mundo con MARS® (Splines de regresión adaptativa multivariante) o mejore sus habilidades utilizando nuestros métodos basados en árboles, como los árboles de clasificación y regresión, más conocidos como CART®, Random Forests® y gradiente potenciado, más conocido como TreeNet®. ¿No está seguro de qué método elegir? Confirme fácilmente que está utilizando el mejor modelo predictivo para responder a su pregunta con el aprendizaje automático automatizado (Auto-ML). Perfecto para aquellos que son nuevos en el análisis predictivo y necesitan recomendaciones, y expertos que buscan una segunda opinión.
CART®Árboles de clasificación y regresión |
|
Como una de las herramientas más importantes y populares en la minería de datos moderna, CART es el árbol de clasificación definitivo. CART y su motor de modelado han revolucionado el campo de la analítica avanzada e inaugurado la era actual de la ciencia de datos.
Para aquellos que son nuevos en CART, se trata de un algoritmo basado en árboles que funciona buscando muchas formas de particionar o dividir datos localmente en segmentos más pequeños en función de diferentes valores y combinaciones de predictores. CART selecciona las divisiones de mejor rendimiento, luego repite este proceso recursivamente hasta que se encuentra la colección óptima. El resultado es un árbol de decisión representado por una serie de divisiones binarias que conducen a nodos terminales que pueden describirse mediante un conjunto de reglas específicas. El árbol y su diseño son visualmente estimulantes e intuitivos de interpretar, por lo que no es necesario ser un científico de datos para comprenderlo y obtener información útil.
Diseñado para usuarios de todos los niveles, el modelo de CART puede revelar rápidamente relaciones importantes que podrían permanecer ocultas al usar otras herramientas analíticas. CART se destaca en el campo del análisis predictivo gracias a su metodología original y altamente deseable que incluye automatización integrada, facilidad de uso, rendimiento y precisión.
Propietario
La metodología de CART se basa en una teoría matemática histórica introducida en 1984 por cuatro estadísticos de renombre mundial en la Universidad de Stanford y la Universidad de California en Berkeley. El motor de modelado CART, la implementación de árboles de clasificación y regresión de Minitab, es el único software de árboles de decisión que incorpora el código patentado original.
Rápido y Versátil
Las extensiones patentadas del motor de modelado CART se diseñaron específicamente para mejorar los resultados de la investigación y el análisis de mercado, respaldar la implementación de alta velocidad y predecir y puntuar en tiempo real. A lo largo de los años, nuestro motor se ha convertido en uno de los algoritmos de modelado predictivo disponibles más populares y fáciles de usar, y es fundamental para muchos enfoques modernos de minería de datos basados en bagging y boosting.
Random Forests®Los bosques aleatorios de Breiman y Cutler |
|
Basado en una colección de árboles de clasificación y regresión (CART®), el motor de modelado Random Forests® suma las predicciones hechas de cada árbol CART para determinar la predicción general del bosque, al tiempo que garantiza que los árboles de decisión no se vean influenciados entre sí.
Para aquellos nuevos en Random Forests, es una potente técnica de conjunto desarrollada por Leo Breiman y Adele Cutler en la Universidad de California, Berkeley, y es favorecida por muchos practicantes de modelos predictivos. La simplicidad engañosa del algoritmo construye cientos de árboles independientes y emplea mucho muestreo de observaciones y variables.
La capacidad única de Random Forests para evaluar el rendimiento imparcial del modelo en función de los datos listos para usar elimina la necesidad de tener una muestra de prueba/validación separada. Esto posiciona inmediatamente a Random Forests como la mejor herramienta de modelado predictivo en las amplias aplicaciones de datos donde la cantidad de variables excede, a menudo muchas veces, la cantidad de observaciones disponibles.
Responsabilidad
Random Forests tiene una capacidad única para aprovechar cada registro en su conjunto de datos sin los peligros del sobreajuste. Esto es especialmente importante para conjuntos de datos pequeños (en términos de observaciones), donde cada registro puede aportar algo valioso. Random Forests se asegurará de que todos los registros se hayan tenido en cuenta en sus modelos y que no se haya perdido ninguna información.
Importancia variable robusta
Random Forests utiliza técnicas novedosas para clasificar los predictores según su importancia. Esto es conveniente cuando los datos incluyen miles, decenas o incluso cientos de miles de variables o predictores, lo que está más allá del alcance de las herramientas de regresión y clasificación convencionales. Random Forest puede manejar situaciones tan extremas e informar qué variables usar en la investigación de seguimiento. Múltiples rondas de muestreo agregarán solidez y calidad a estos conocimientos.
TreeNet®Aumento de gradiente |
|
La herramienta de aprendizaje automático más flexible, galardonada y potente de Minitab, TreeNet® Gradient Boosting, es capaz de generar modelos extremadamente precisos de manera consistente.
Para aquellos que son nuevos en TreeNet, es una potente implementación de la moderna clase de algoritmos de aprendizaje automático generalmente conocida como Stochastic Gradient Boosting. Desarrollada por Jerome Friedman en la Universidad de Stanford, la técnica es conocida por su excelente precisión predictiva. El secreto está en la forma en que se construye un modelo: en cada iteración se agrega un pequeño árbol al conjunto actual de árboles para corregir los errores combinados del conjunto.
Utilizando la variedad de funciones de pérdida suministradas, el proceso puede ajustarse para la tarea específica de modelado predictivo, como regresión de mínimos cuadrados, regresión robusta, clasificación, etc. Para ayudar con la interpretación del modelo, TreeNet va un paso más allá y genera automáticamente varios 2D y gráficos 3D para explicar la naturaleza de la dependencia de la variable de respuesta en las entradas del modelo. El modelo es lo suficientemente flexible para descubrir e incorporar automáticamente varias no linealidades e interacciones multidireccionales. Un conjunto adicional de controles permite al usuario ajustar las interacciones del modelo para cumplir con los objetivos de diseño específicos.
Precisión incomparable
Nuestro motor de modelado TreeNet tiene un grado de precisión generalmente inalcanzable por un solo modelo o conjuntos, como embolsado o refuerzo convencional. Nuestra metodología no es sensible a los errores de datos y no requiere preparación de datos, preprocesamiento o imputación de valores faltantes que consumen mucho tiempo. Con otros métodos, los errores de datos pueden ser un desafío para la minería de datos convencional y catastróficos para el impulso convencional. Por el contrario, el modelo TreeNet es inmune a tales errores, ya que rechaza dinámicamente los datos que difieren demasiado del modelo existente o que están contaminados con etiquetas objetivo erróneas.
Perspectivas ilustradas
Evite las técnicas convencionales de prueba y error o caminar en la oscuridad en el futuro. Nuestro motor de modelado TreeNet ofrece un conjunto único de información sobre el funcionamiento interno de sus modelos con gráficos de dependencia. Nuestras gráficas de dependencia parcial en 2D muestran la naturaleza de los efectos principales, mientras que nuestras gráficas de dependencia parcial en 3D también incluyen interacciones bidireccionales. Armado con los nuevos conocimientos descubiertos automáticamente por TreeNet, podrá crear modelos de regresión y clasificación de alta precisión si es necesario.
Detección de interacción
La detección de interacciones dentro de nuestro motor de modelado TreeNet establece si se necesitan interacciones de algún tipo en un modelo predictivo. Este sistema no solo ayuda a mejorar el rendimiento del modelo, a menudo de forma espectacular, sino que también ayuda a descubrir y utilizar nuevos conocimientos valiosos.
MARS®Splines de regresión adaptativa multivariable |
|
El motor de modelado MARS® es ideal para los usuarios que prefieren los resultados en una forma similar a la regresión tradicional, pero sin dejar de detectar las no linealidades y las interacciones esenciales.
El enfoque de modelado de regresión de la metodología MARS revela de manera efectiva patrones y relaciones importantes en los datos que son difíciles, si no imposible, de revelar para otros métodos de regresión. El motor de modelado MARS construye su modelo juntando una serie de líneas rectas, donde cada una puede tener su propia pendiente. Esto permite que el motor de modelado MARS trace cualquier patrón detectado en los datos.
Regresión y clasificación de alta calidad
El modelo MARS está diseñado para predecir resultados numéricos, como la factura mensual promedio de un cliente de telefonía móvil o la cantidad que se espera que un comprador gaste en una visita a un sitio web. El motor MARS también es capaz de producir modelos de clasificación de alta calidad para un resultado sí/no. El motor MARS realiza selección de variables, transformación de variables, detección de interacciones y autoevaluaciones, todo de manera automática y a gran velocidad.
Resultados de alto rendimiento
Las áreas en las que el motor MARS ha exhibido resultados de muy alto rendimiento incluyen la predicción de la demanda de electricidad para empresas generadoras de energía, la asociación de las puntuaciones de satisfacción de los clientes con las especificaciones técnicas de los productos y el modelado de presencia/ausencia en los sistemas de información geográfica (SIG).
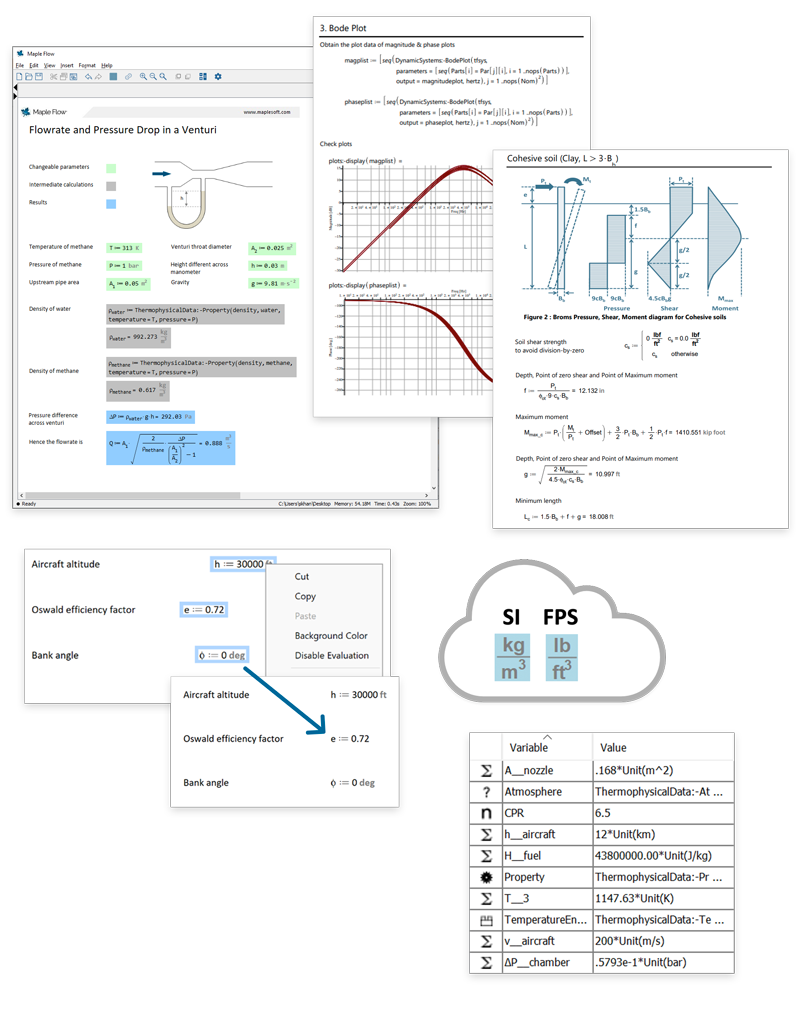
- Detalles
- Categoría: Maple
- Visto: 4805
- Detalles
- Categoría: MapleSim
- Visto: 5612
Con las complejas interconexiones entre los componentes mecánicos y eléctricos y las dificultades inherentes a los problemas de modelado multicuerpo, se requiere experiencia, habilidad y las herramientas adecuadas para llevar a cabo sus proyectos de robótica y mecatrónica a tiempo y dentro del presupuesto. Maplesoft puede ayudar. Las soluciones de ingeniería de Maplesoft le brindan la experiencia y las herramientas que necesita para reducir el riesgo de desarrollo y llevar productos de alta calidad al mercado más rápido.

Soporte de soluciones de ingeniería de Maplesoft:
Validación a nivel de sistema de diseños de robótica y mecatrónica
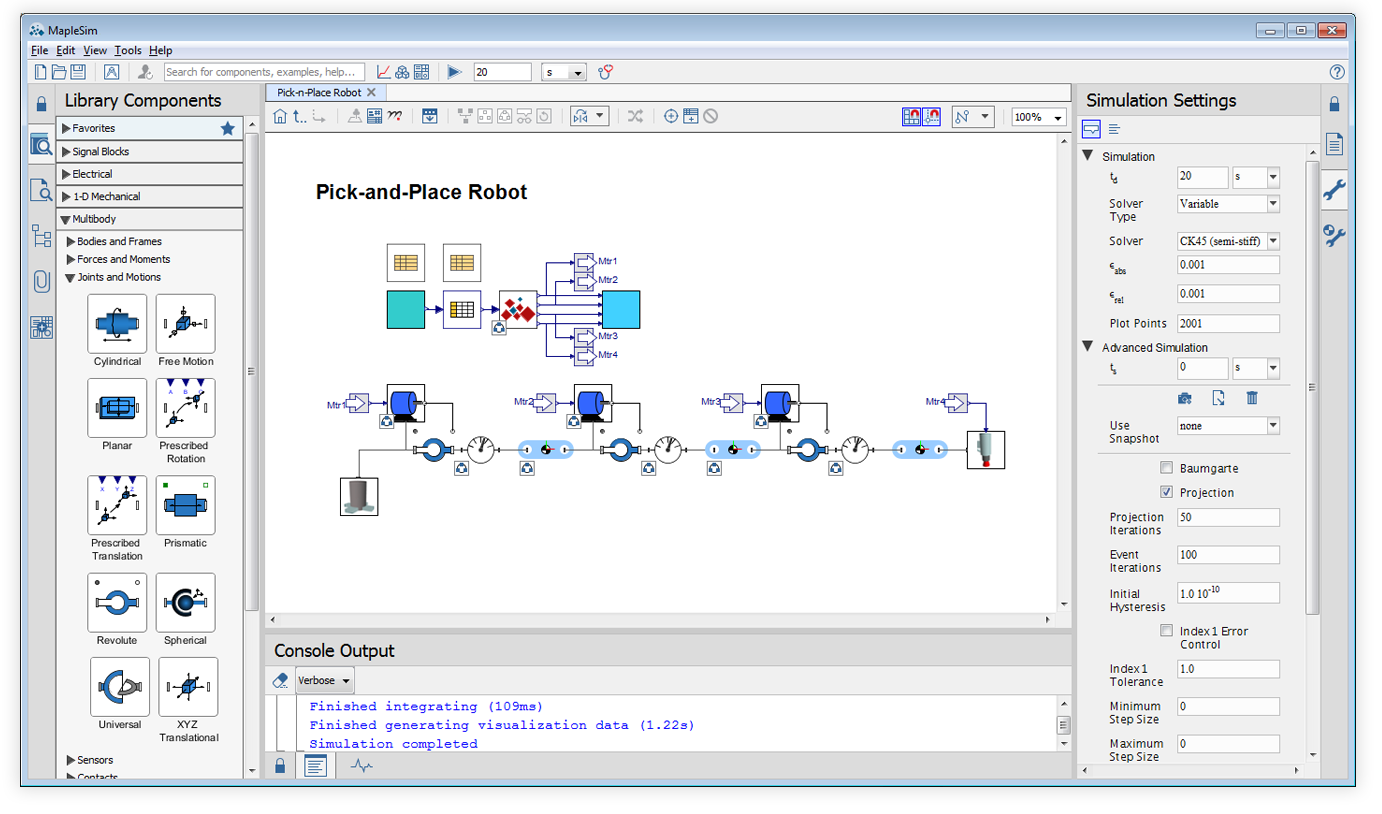 |
Mediante el uso de modelado y simulación a nivel de sistema de alta fidelidad, las soluciones de ingeniería de Maplesoft lo ayudan a determinar cómo se comportará su diseño utilizando un prototipo "virtual" de su sistema. De esta forma, es posible validar su diseño contra las especificaciones y corregir cualquier falla mucho antes de invertir en un prototipo físico, ahorrando mucho tiempo y dinero. Maplesoft Engineering Solutions también puede ayudar a investigar formas de mejorar aún más su diseño. Debido a que nuestros productos brindan acceso a las ecuaciones subyacentes que representan el comportamiento físico de su diseño, pueden usarse para desarrollar herramientas de análisis paramétrico personalizadas incluso para sistemas complejos de múltiples dominios. Estas herramientas brindarán a sus ingenieros información importante sobre el efecto de los cambios de parámetros en el sistema general, lo que les permitirá optimizar su diseño. Además, puede aprovechar los barridos de parámetros automatizados, el análisis de Monte Carlo, los estudios de sensibilidad, el diseño de experimentos y la optimización multiobjetivo, para que pueda mejorar sus productos y sentirse seguro en sus elecciones de diseño. |
Flexibilidad y control de modelos sin igual a través de la revolucionaria tecnología multicuerpo
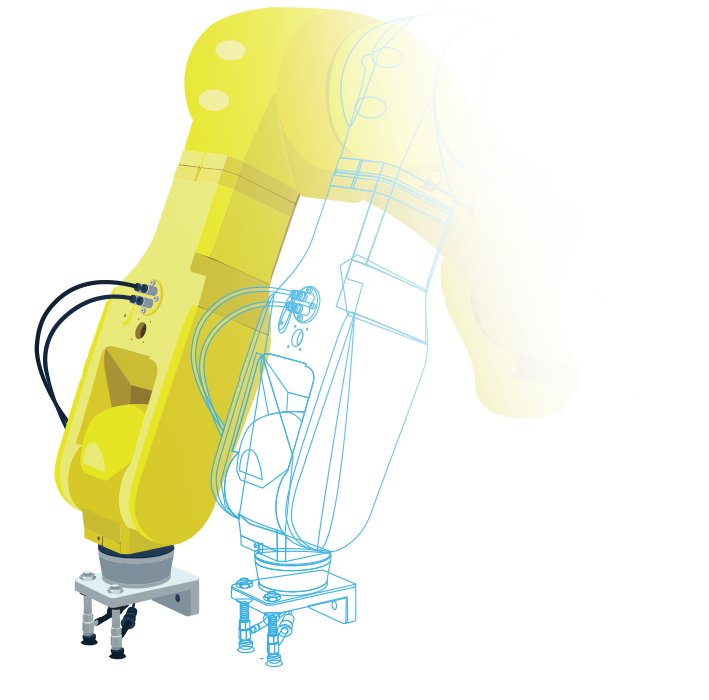 |
Los prototipos a nivel de sistema ahorran tiempo y dinero porque con frecuencia surgen problemas de las interacciones de los subsistemas, incluso cuando cada subsistema cumple con sus propios requisitos de diseño. Al utilizar Maplesoft Engineering Solutions, puede crear prototipos virtuales multidominio a nivel de sistema para abordar este tipo de problemas de diseño mucho antes de invertir en costosos prototipos físicos e incluso realizar mejoras en el diseño general. El uso de este enfoque le permite reducir el riesgo de desarrollo, crear mejores productos y llegar al mercado más rápido. |
Código de modelo optimizado para simulaciones en el ciclo
 |
Ya sea que se esté trabajando en aplicaciones de hardware, software o operador en el ciclo, es fundamental que los modelos del sistema se ejecuten en una plataforma en tiempo real dentro del paso de tiempo de simulación. La formulación de modelos simbólicos y las técnicas de generación de código optimizadas disponibles con Maplesoft Engineering Solutions garantizan el tiempo de ejecución más rápido posible para el modelo. Sin embargo, con sistemas grandes, incluso el tiempo más rápido posible puede no ser lo suficientemente rápido. Cuando eso sucede, la amplia experiencia de Maplesoft en técnicas rigurosas de reducción de modelos y optimización de código, maximizan la fidelidad dentro de las limitaciones de trabajar en una plataforma en tiempo real. |
Herramientas de cálculo de análisis y diseño
Muchos proyectos requieren la creación de herramientas especializadas de análisis y cálculo para respaldar la toma de decisiones informadas, como herramientas para el análisis y la atenuación de vibraciones, el análisis térmico y el dimensionamiento de componentes, entre muchas otras. Las soluciones de ingeniería de Maplesoft permiten el desarrollo de poderosas herramientas analíticas para brindarle a su equipo las respuestas que necesitarán en los años venideros. Según sus necesidades, estas herramientas pueden ser aplicaciones especializadas destinadas a ser utilizadas por expertos o soluciones llave en mano fáciles de usar adecuadas para una implementación más amplia en toda su organización.
Soluciones analíticas a problemas de cinemática inversa y dinámica inversa
En mecánica multicuerpo, el análisis del movimiento de una plataforma (el problema de la cinemática) se puede clasificar en dos casos: el problema de la cinemática directa y el problema de la cinemática inversa. En general, es bastante sencillo resolver el problema de cinemática directa tanto numérica como simbólicamente.
Por el contrario, resolver el problema de la cinemática inversa es más complejo. Debido a la complejidad involucrada, el problema de cinemática inversa a menudo se resuelve numéricamente a través de iteraciones y es computacionalmente costoso. Sin embargo, con un enfoque numérico, a menudo se pierde información sobre el movimiento del mecanismo. En este artículo, describiremos cómo obtener una solución simbólica al problema de cinemática inversa para un manipulador de enlaces paralelos de Stewart-Gough usando herramientas disponibles en MapleSim.
|
En todo el mundo, los clientes en una amplia gama de industrias y disciplinas técnicas están utilizando las soluciones de Maplesoft para acelerar rápidamente sus proyectos de diseño, mientras desarrollan la próxima generación de productos que dan forma a la cara cambiante de la robótica:
Estas y muchas otras historias están disponibles en esta colección. ¡Solicítenosla! |
 |
- Detalles
- Categoría: Comsol
- Visto: 6728
Cuando se trabaja con una interfaz física en COMSOL, en la parte de ajustes, existe una sección de Discretización. Allí se puede escoger el orden de elemento que se está utilizando. Esta ocasión abordaremos el tema del orden de los elementos y la discretización para una simulación. Esta elección es importante porque tiene efectos en la malla y la solución del modelo.
¿Qué significan el orden y la discretización de los elementos?
La mayoría de las interfaces de física dentro de COMSOL Multiphysics utilizan el método de elementos finitos para resolver las ecuaciones diferenciales parciales subyacentes. El método de elementos finitos funciona discretizando los dominios de modelado en dominios más pequeños y simples llamados elementos. La solución se calcula ensamblando y resolviendo un conjunto de ecuaciones sobre todos los elementos del modelo. La solución de estas ecuaciones se aproxima a la solución real de la ecuación diferencial parcial.
Las ecuaciones dentro de cada elemento también se conocen como funciones de forma y pueden ser de distinto orden. Por ejemplo, en el caso más simple de un modelo de elementos finitos unidimensional, las funciones de forma dentro de cada elemento son simplemente un conjunto de polinomios definidos sobre el dominio. En la imagen siguiente se representa el conjunto de funciones de forma lineales (primer orden), cuadráticas (segundo orden) y cúbicas (tercer orden). La solución dentro de los elementos se basa en una suma lineal de estas funciones de forma. Ver Fig. 1.
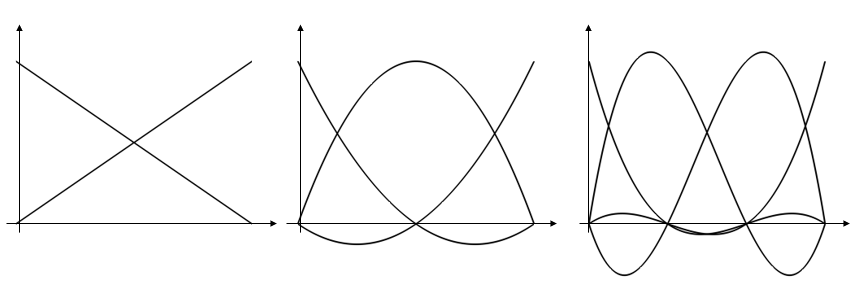
Fig. 1. Gráficos de funciones de forma lineal (izquierda), cuadrática (centro) y cúbica (derecha) en un elemento unidimensional (imagen obtenida del Blog de COMSOL [1]).
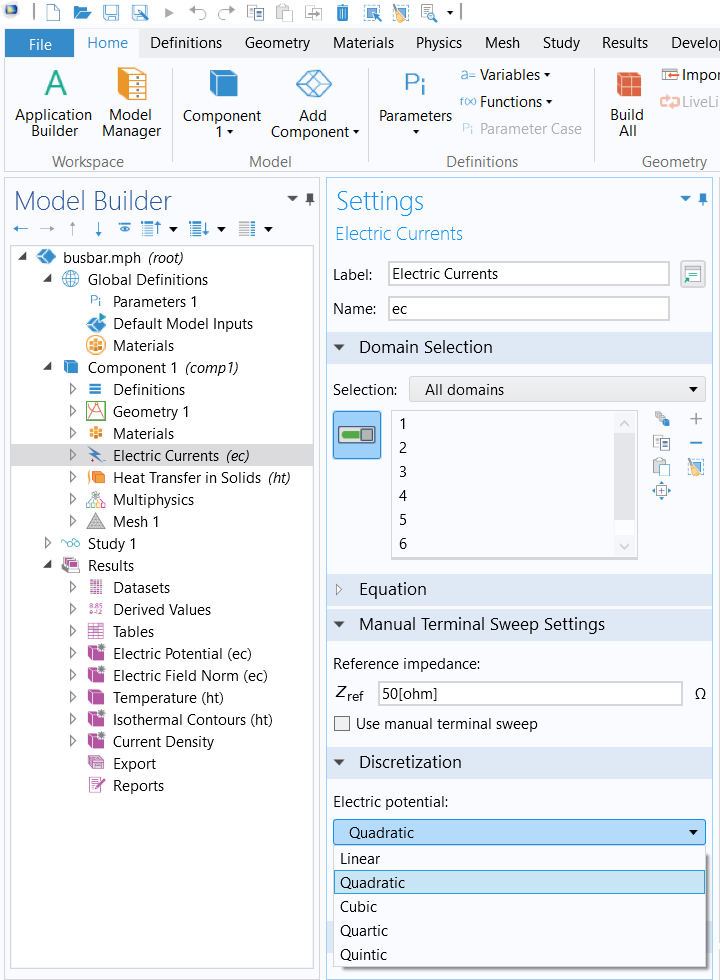
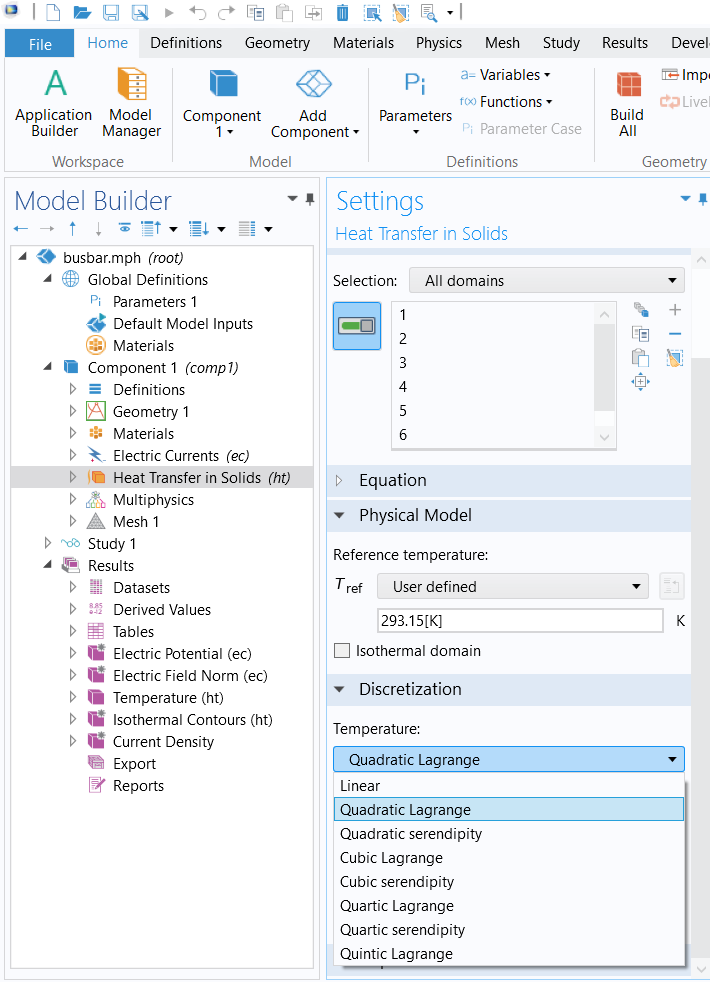
Un modelo que contiene varias interfaces físicas puede utilizar diferentes conjuntos de funciones de forma. Es decir, cada interfaz de física tiene sus propios ajustes de discretización únicos que gobiernan qué funciones de forma de orden se utilizan para esas variables dependientes, como se muestra en la captura de pantalla del ejemplo a continuación para la interfaz de física de Corrientes Eléctricas y Heat Transfer in Solids (Fig. 2).
 |
 |
|
Fig. 2. Funciones de forma utilizadas en el desplegable de discretización en la interfaz de Electric Currents (izquierda) y en la interfaz de Heat Transfer in Solids (derecha). En ambos casos se trata del modelo Busbar de la librería de aplicaciones. Ver [2]. |
|
La discretización por defecto en muchos casos es de segundo orden (cuadrática), y esto se debe en parte a que muchas de las ecuaciones diferenciales parciales tienen un término de segunda derivada dominante. Los problemas de flujo y transporte de fluidos suelen utilizar por defecto una discretización lineal de primer orden. Basado en la situación particular de modelado, cambiar la discretización puede estar motivado, y es posible cambiar la discretización para cada interfaz física diferente independientemente, pero hacerlo tiene varias consecuencias. Disminuir la discretización sin cambiar el número de elementos conducirá a un modelo que requiere menos recursos computacionales, pero tendrá menor precisión. Aumentar la discretización sin cambiar el número de elementos conducirá a una solución más precisa, pero requerirá mayores recursos computacionales. Se debe tener en cuenta que el aumento del orden de los elementos es un enfoque para validar el modelo, pero que es probable que desee estudiar el refinamiento de la malla mediante la realización de un estudio de refinamiento de malla.
Efecto en la malla
Al modelar en 2D, axis simétrico 2D o 3D, los ajustes de discretización dentro de la física también afectan a los elementos de malla. Los elementos de malla en 2D y 3D sirven además para aproximar la geometría CAD real, y lo hacen aproximando la forma de los contornos del modelo mediante un conjunto de funciones de forma geométrica que tienen el mismo orden que el orden de discretización más bajo utilizado en cualquiera de las interfaces de física habilitadas dentro del modelo.
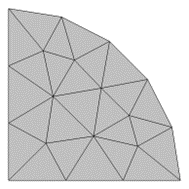
Lo anterior se puede visualizar considerando un dominio semicircular, discretizado con la malla más simple posible consistiendo en un único elemento triangular. Los lados rectos del dominio de modelado se representan con precisión sin importar las funciones de forma, pero el contorno curvo sólo puede representarse aproximadamente mediante las funciones de forma geométrica. Con una función de forma lineal, esta aproximación se reduce a un elemento triangular que representa bastante mal el dominio de modelización. Las funciones de forma cuadrática y cúbica ofrecen una representación mucho mejor de la geometría subyacente. Una consecuencia de esto es que, cuando se utilizan funciones de forma de geometría lineal, generalmente se necesita una malla mucho más fina en los límites curvos sólo para obtener una representación precisa de la geometría CAD subyacente.
De acuerdo con el Blog de COMSOL [3], una buena regla general, cuando se utilizan funciones de forma de geometría lineal, se necesitan al menos 8 elementos por arco de 90° para resolver el límite con menos del 1% de error. Por otro lado, con funciones de forma cuadráticas y de orden superior, incluso dos elementos por arco de 90° son suficientes para representar la geometría CAD con un error significativamente inferior al 1%. Estas reglas empíricas son sólo puntos de partida sobre cómo crear una malla inicial; siempre es necesario un estudio de refinamiento de la malla [3]. Notar que, al construir y visualizar la malla, los elementos aparecerán siempre con lados rectos, aunque las funciones de forma subyacentes sean de orden superior. Sólo cuando se trazan los resultados, los límites de los elementos se trazarán de forma que muestren la función de forma subyacente (ver Fig. 3)
 |
 |
|
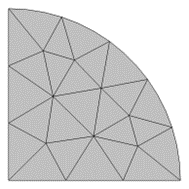
Fig. 3. Se malla un dominio semicircular utilizando una función de forma lineal de Lagrange (izquierda) y Lagrange cúbica (derecha). Se observa la diferencia en la representación de la frontera curva. |
|
Más información sobre la inspección de los elementos de malla se puede ver en [4].
Referencias
[1] https://www.comsol.com/support/learning-center/article/Understanding-and-Changing- the-Element-Order-64391
[2] https://www.comsol.com/model/electrical-heating-in-a-busbar-10206
[3] https://www.comsol.com/support/knowledgebase/1261
[4] https://www.comsol.com/blogs/how-to-inspect-your-mesh-in-comsol-multiphysics/
- Detalles
- Categoría: Minitab
- Visto: 11014
Por Stacey McDaniel
Aunque a menudo viajan en los mismos círculos, la mejora continua y la calidad no son lo mismo. Si bien la mejora continua y la calidad están relacionadas, tienen objetivos diferentes. Profundicemos y analicemos esas diferencias con respecto a la fabricación y las herramientas que se utilizan para lograr ambas.
- La calidad de fabricación se refiere al nivel de excelencia en el proceso de producción y el producto final, asegurando que cumple o supera las especificaciones deseadas. La calidad se puede definir de varias maneras, como confiabilidad, durabilidad, rendimiento, seguridad y facilidad de uso.
- La mejora continua identifica áreas de mejora, analiza las causas raíz e implementa cambios para eliminar desperdicios, reducir costes y aumentar la productividad.
Si bien ambas son componentes esenciales de una fabricación exitosa, la garantía de calidad garantiza que el producto final cumpla con el estándar deseado, mientras que la mejora continua se enfoca en hacer que el proceso de producción sea más eficiente y efectivo, lo que lleva al éxito y la sostenibilidad a largo plazo. Existen diferencias similares en la calidad del diseño y la mejora continua en la oficina, no solo en la fabricación específicamente. En resumen, la calidad de fabricación es un resultado, mientras que la mejora continua es un proceso continuo.
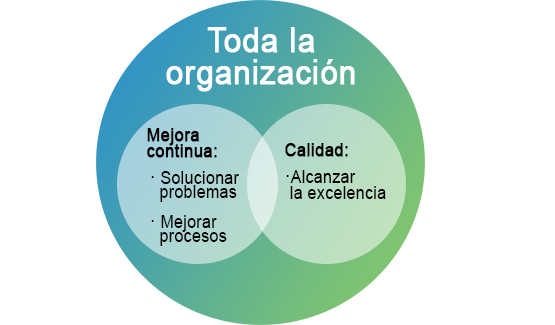
Donde mejora continua y calidad se superponen
La mejora continua es un factor clave de la calidad. Al esforzarse constantemente por mejorar los procesos, productos y servicios, las organizaciones crean resultados de mayor calidad. Alternativamente, la calidad es un objetivo clave de la mejora continua. Al implementar procesos de mejora continua, las organizaciones pueden mejorar la calidad al identificar y abordar los problemas antes de que se conviertan en problemas mayores.
DIFERENTES METODOLOGÍAS UTILIZADAS
Se utilizan diferentes metodologías para la calidad y la mejora continua, pero también hay cierta superposición, como se verá:
- Para asegurar la calidad, se utilizan comúnmente metodologías como Six Sigma, Gestión de calidad total (TQM), Control estadístico de procesos (SPC) y Lean Manufacturing. Estas metodologías se enfocan en identificar y eliminar defectos, reducir la variabilidad y mejorar la estabilidad del proceso para lograr resultados de producción consistentes y de alta calidad.
- Las metodologías de mejora continua como Kaizen y Lean Manufacturing se enfocan en optimizar el proceso de producción para eliminar desperdicios, reducir los tiempos de ciclo y mejorar la eficiencia. Estas metodologías se basan en un enfoque de resolución de problemas que implica identificar oportunidades de mejora, probar soluciones potenciales e implementar cambios en un circuito de retroalimentación continuo.
Tanto las metodologías de garantía de calidad como las de mejora continua están diseñadas para mejorar los procesos de fabricación y mejorar la calidad del producto. Sin embargo, las técnicas y herramientas específicas utilizadas pueden diferir según las metas y objetivos específicos de cada enfoque.
EN QUÉ SE DIFERENCIAN LAS HERRAMIENTAS
Las herramientas de calidad y las herramientas de mejora continua son esenciales para diferentes aspectos de la investigación para mejorar los procesos y la calidad.
- Las herramientas de calidad se utilizan para garantizar que los resultados de la investigación sean precisos, fiables y válidos. Pueden ayudar a identificar posibles fuentes de sesgo, medir la coherencia de la recopilación de datos y evaluar la precisión de los análisis estadísticos. Los ejemplos de herramientas de calidad utilizadas en la investigación incluyen gráficos de control, gráficos de Pareto, diagramas de Ishikawa y control estadístico de procesos.
- Se utilizan herramientas de mejora continua para optimizar el proceso de investigación, haciéndolo más eficiente y eficaz. Pueden ayudar a identificar áreas de desperdicio, reducir los tiempos de ciclo y mejorar la productividad. Los ejemplos de herramientas de mejora continua utilizadas en la investigación incluyen Kaizen, Lean Manufacturing y el ciclo Plan-Do-Check-Act (PDCA).
Tanto las herramientas de calidad como las de mejora continua son necesarias para asegurar la calidad de la investigación y mejorar el proceso de investigación. Las herramientas de calidad ayudan a garantizar la precisión y validez de los resultados de la investigación, mientras que las herramientas de mejora continua ayudan a optimizar el proceso de investigación para lograr mejores resultados con menos tiempo y esfuerzo. Por lo tanto, los investigadores deben usar ambos tipos de herramientas para lograr resultados de investigación de alta calidad.
Como puede ver, la mejora continua y la calidad son muy diferentes, y no puede tenerse una sin la otra. Si desea ver cómo Minitab puede ayudar en sus iniciativas de calidad o mejora continua, ¡comuníquese con nosotros!
- Detalles
- Categoría: Lakes
- Visto: 4482
CALRoads View hace que sea muy fácil introducir enlaces a un proyecto de modelado utilizando una de las series de modelos CALINE (CALINE, CAL3QHC, CAL3QHCR). Si bien es común representar enlaces gráficamente, CALRoads también permite a los modeladores importar enlaces usando una plantilla de hoja de cálculo de Excel. Esto es útil para los modeladores que tienen todas sus entradas definidas o aquellos que tienen muchos datos para incluir. La hoja de cálculo plantilla se encuentra en la carpeta C:\Lakes\CALRoads View\Templates.
Una funcionalidad nueva es la capacidad de importar enlaces de grupo (G-Links). La columna T de la hoja de cálculo presenta una columna Group.
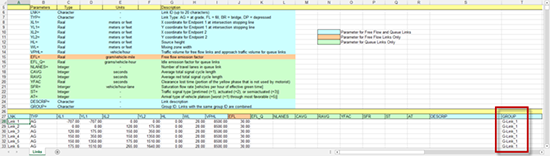
Para definir enlaces de grupo, especifique Group ID para varios enlaces. Utilice el mismo ID de grupo en todos los enlaces del grupo. Se pueden importar varios enlaces de grupo mediante el uso de un ID de grupo único para cada enlace de grupo.
- Detalles
- Categoría: Comsol
- Visto: 2780
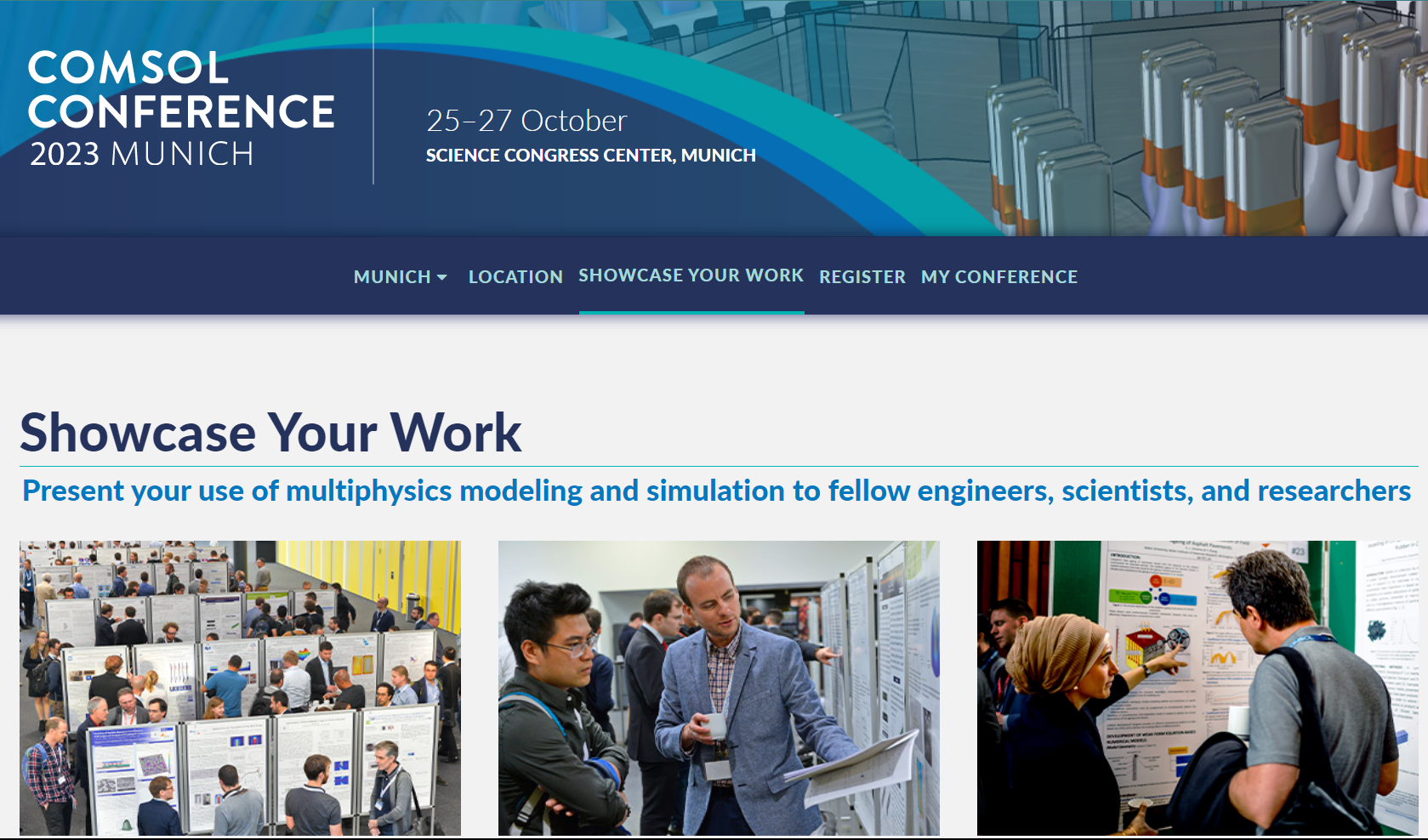
El plazo de entrega anticipada de resúmenes en la conferencia COMSOL Conference 2023, que supone un gran descuento en el registro a la conferencia está próximo a su fin.
Envíe su resumen antes del viernes, 9 de junio y tanto Vd. como los coautores del trabajo podrán optar a un precio de registro reducido (ahorro de 150€).
¡No pierda esta oportunidad para mostrar sus investigaciones e ideas a una audiencia global de expertos en simulación e ingenieros!
Para obtener las guías, plantillas y entregar su resumen, visite la web de la conferencia