- Detalles
- Categoría: Minitab
- Visto: 704
Minitab, LLC, líder mundial en análisis de datos, análisis predictivo y mejora continua de procesos, ha dado un paso decisivo hacia el futuro de la analítica con la incorporación de tres soluciones que transforman la manera en que las organizaciones abordan la resolución de problemas basada en datos: Minitab Solution Center™, Prolink y Simul8. Estas incorporaciones refuerzan el compromiso de la compañía con la innovación, la eficiencia y la excelencia operativa, consolidando su posición como socio estratégico de referencia para las empresas que buscan convertir los datos en decisiones inteligentes.
Con estas tres nuevas incorporaciones, Minitab no solo amplía su cartera tecnológica, sino que también redefine el alcance de su ecosistema analítico, unificando herramientas en la nube, automatizando la recopilación de datos y añadiendo simulación avanzada y gemelos digitales a su oferta. Cada uno de estos productos aporta un valor único y complementario, diseñado para potenciar el flujo de trabajo integral de los usuarios y llevar la mejora continua a un nuevo nivel.
1. Minitab Solution Center™: la nueva plataforma unificada de soluciones en la nube
Minitab Solution Center™ representa el núcleo de esta nueva era para Minitab. Se trata de una plataforma integral basada en la nube que unifica todas las soluciones de la compañía en un solo lugar, facilitando la resolución de problemas basada en datos de forma ágil, colaborativa y centralizada. Esta innovación permite a los usuarios acceder desde un entorno único a herramientas de análisis, visualización, inteligencia artificial y aprendizaje continuo, optimizando la toma de decisiones en todos los niveles de la organización.
Un ecosistema de análisis unificadoEn el corazón del Minitab Solution Center se encuentra el Software Estadístico Minitab, la herramienta insignia de la compañía, reconocida por su potencia analítica y su facilidad de uso. A partir de esta base, el nuevo centro amplía su alcance con tres pilares complementarios: |
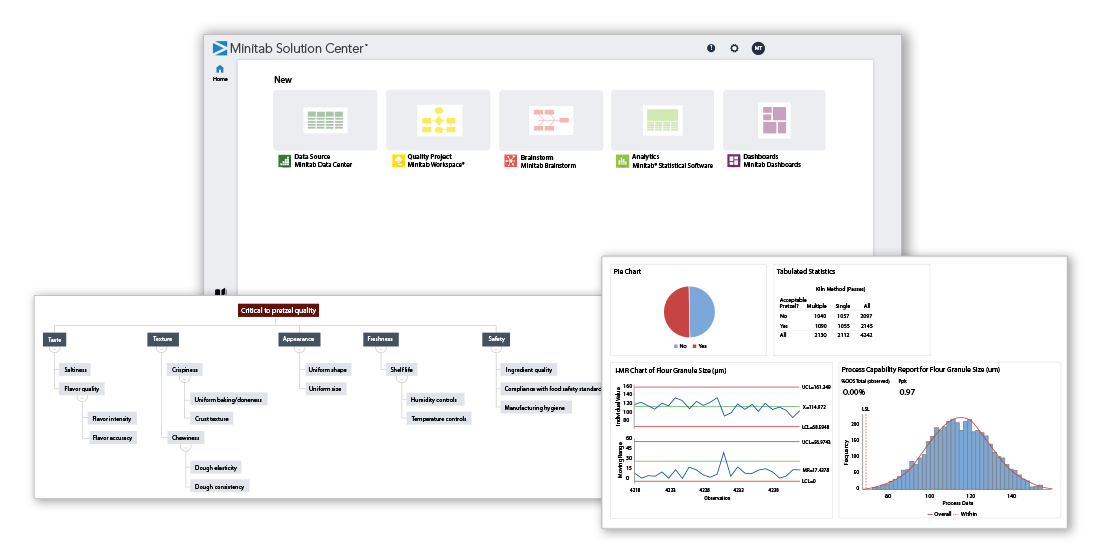 |
- Minitab Data Center (Centro de Datos de Minitab)
Diseñado para acelerar el análisis y la exploración de la información, el Centro de Datos ofrece visualizaciones interactivas e intuitivas que permiten obtener información inmediata. Su interfaz simplifica la preparación y el tratamiento de datos, ayudando a los usuarios a centrarse en lo verdaderamente importante: entender y utilizar los datos para mejorar procesos y tomar decisiones informadas. - Minitab Dashboards (Tableros de Control de Minitab)
Los nuevos tableros transforman los datos sin procesar en información práctica y dinámica, mediante gráficos interactivos que facilitan la interpretación y el intercambio de resultados entre equipos. Gracias a su actualización automática, los usuarios pueden monitorear indicadores clave en tiempo real y responder con agilidad a los cambios en el rendimiento. - Minitab Brainstorm
Esta funcionalidad impulsa la creatividad y la resolución colaborativa de problemas, ofreciendo plantillas de eficacia probada como mapas mentales, diagramas de causa y efecto (Ishikawa) y árboles de importancia crítica para la calidad (CTQ). Su integración dentro del entorno analítico de Minitab permite que las ideas generadas se conecten directamente con los datos y el análisis estadístico, cerrando el ciclo entre la ideación y la acción.
Minitab AI™: inteligencia artificial al servicio de la comprensión
Una de las incorporaciones más revolucionarias dentro del Minitab Solution Center es Minitab AI™, una inteligencia artificial diseñada no para reemplazar el análisis humano, sino para potenciarlo. Esta herramienta genera resúmenes en lenguaje natural de los resultados estadísticos, ayudando a los usuarios a comprender rápidamente los hallazgos y centrarse en la interpretación y las decisiones estratégicas.
Además, Minitab AI se integra en el módulo Brainstorm, mejorando las sesiones de lluvia de ideas con sugerencias automatizadas que estimulan la creatividad colectiva de los equipos. De este modo, la inteligencia artificial se convierte en un aliado que impulsa la eficiencia, la colaboración y la confianza en los resultados.
Centro de aprendizaje y recursos guiados
El Centro de aprendizaje de Minitab completa esta experiencia con un repositorio de recursos interactivos, tutoriales, consejos de expertos y contenido guiado. Su objetivo es fomentar el aprendizaje continuo y garantizar que los usuarios aprovechen al máximo cada herramienta de la plataforma.
Con Minitab Solution Center™, la compañía consolida un entorno analítico de nueva generación: flexible, colaborativo, inteligente y accesible desde cualquier lugar.
2. Prolink: automatización y control de calidad en tiempo real
La segunda gran incorporación al portfolio de Minitab es Prolink, una empresa líder con más de 40 años de experiencia en la automatización de la recopilación de datos de equipos de inspección y el control estadístico de procesos (SPC). Su integración en el ecosistema Minitab amplía significativamente las capacidades de la compañía en el ámbito del control de calidad y la manufactura inteligente.
La biblioteca de controladores más completa del mercadoUno de los grandes diferenciadores de Prolink es su biblioteca de controladores, la más extensa del mundo, capaz de conectarse automáticamente con más de 320 marcas, modelos y versiones de equipos de inspección automática, incluyendo máquinas de medición por coordenadas (MMC), medidores, sistemas de visión y controladores lógicos programables (PLC). Esta conectividad permite recopilar datos en tiempo real sin intervención manual, eliminando errores humanos y mejorando la trazabilidad y la fiabilidad de la información. Los resultados se envían automáticamente a las soluciones de Minitab, donde pueden analizarse para identificar causas raíz, tendencias y oportunidades de mejora continua. |
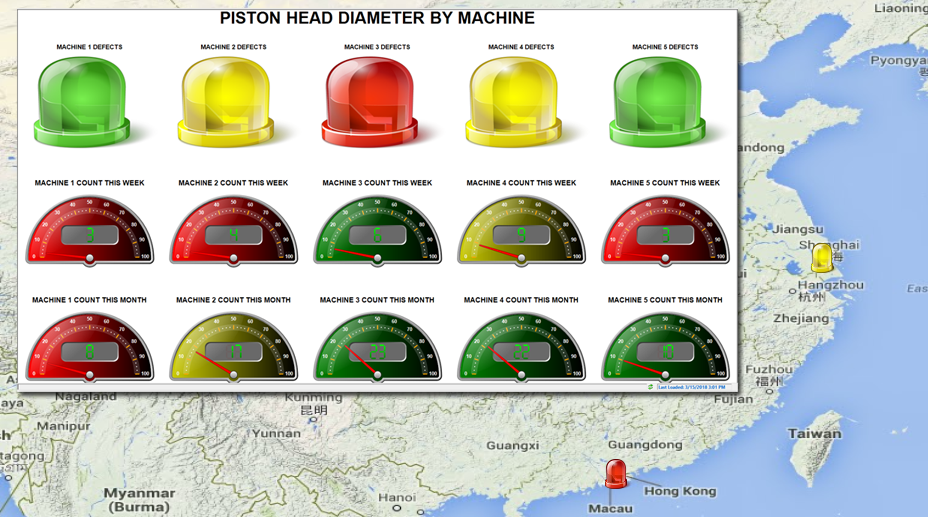 |
Integración perfecta con Minitab para análisis avanzados
La unión de Prolink con Minitab crea una potente sinergia entre la recopilación automatizada de datos y el análisis estadístico avanzado. Ahora, los usuarios pueden conectar sus equipos de inspección directamente con el software de Minitab, cerrando el ciclo entre la medición y la toma de decisiones. Esta integración acelera los tiempos de respuesta, permite detectar desviaciones de calidad en tiempo real y garantiza la consistencia del proceso productivo.
Un paso hacia la Industria 4.0
La automatización que ofrece Prolink coloca a Minitab en el corazón de la transformación digital de la producción. La capacidad de recopilar, integrar y analizar datos directamente desde el punto de producción refuerza las estrategias de Industria 4.0, donde la información fluye sin interrupciones desde la máquina hasta el análisis, generando una visión en tiempo real del rendimiento y la calidad.
Con Prolink, Minitab no solo amplía sus capacidades, sino que también ofrece una solución integral para la gestión de la calidad total (TQM), alineada con las demandas de precisión, velocidad y eficiencia del entorno industrial moderno.
3. Simul8: simulación, gemelos digitales y minería de procesos
El tercer gran avance de Minitab proviene de la adquisición de Simul8 Corporation, una reconocida empresa de software de simulación con sede en Glasgow, Escocia. Esta integración añade un nuevo nivel de sofisticación a las soluciones analíticas de Minitab, incorporando simulación de eventos discretos, gemelos digitales y minería de procesos a su portfolio.
 |
Modelar, predecir y optimizarEl software de Simul8 permite a las organizaciones modelar digitalmente sus procesos, experimentar con distintos escenarios y optimizar operaciones antes de implementarlas en el mundo real. Gracias a su tecnología de simulación de eventos discretos, las empresas pueden prever cuellos de botella, evaluar el impacto de cambios operativos y tomar decisiones basadas en evidencia sin arriesgar recursos ni detener la producción. Además, la funcionalidad de gemelos digitales permite crear representaciones virtuales precisas de procesos, líneas de producción o flujos logísticos, lo que facilita la planificación estratégica, la mejora continua y la gestión de riesgos. |
Minería de procesos para descubrir oportunidades ocultas
Simul8 también ofrece herramientas avanzadas de minería de procesos, que permiten visualizar y analizar cómo fluyen realmente las operaciones dentro de una organización. A través de algoritmos y modelos de simulación, es posible identificar desviaciones, ineficiencias o pasos redundantes, lo que abre la puerta a mejoras sustanciales en la eficiencia y el rendimiento global.
La integración de Simul8 con el ecosistema de Minitab crea una sinergia sin precedentes: los usuarios pueden combinar análisis estadístico, simulación y predicción para obtener una comprensión integral de sus procesos y actuar con mayor precisión.
Un ecosistema integrado para la excelencia empresarial
Con el lanzamiento del Minitab Solution Center y la adquisición de Prolink y Simul8, Minitab consolida un ecosistema analítico integral que abarca todo el ciclo de vida de los datos: desde su captura automática, hasta su análisis avanzado, visualización, simulación y mejora continua.
Esta integración de capacidades permite a las organizaciones:
- Acceder a soluciones basadas en la nube que centralizan el análisis y la toma de decisiones.
- Automatizar la recopilación y el flujo de datos desde los equipos de producción.
- Simular y optimizar procesos antes de su implementación real.
- Aprovechar la inteligencia artificial y el aprendizaje continuo para potenciar el conocimiento organizacional.
- Aumentar la eficiencia operativa, reducir costos y mejorar el rendimiento global.
Con estas incorporaciones, Minitab no solo reafirma su liderazgo histórico en análisis de datos, sino que también se posiciona como la primera plataforma integral de resolución de problemas basada en datos del mundo, donde la innovación, la inteligencia artificial, la automatización y la simulación trabajan juntas para impulsar el éxito de las organizaciones.
En resumen, el lanzamiento de Minitab Solution Center, junto con las adquisiciones de Prolink y Simul8, marca una transformación estratégica para Minitab y sus clientes. La compañía refuerza su visión de ofrecer herramientas que no solo analicen datos, sino que conecten la información, las personas y los procesos para generar valor tangible. En un entorno cada vez más complejo y digitalizado, Minitab demuestra que el futuro del análisis de datos está en la integración inteligente y la acción informada.
- Detalles
- Categoría: Maple
- Visto: 512
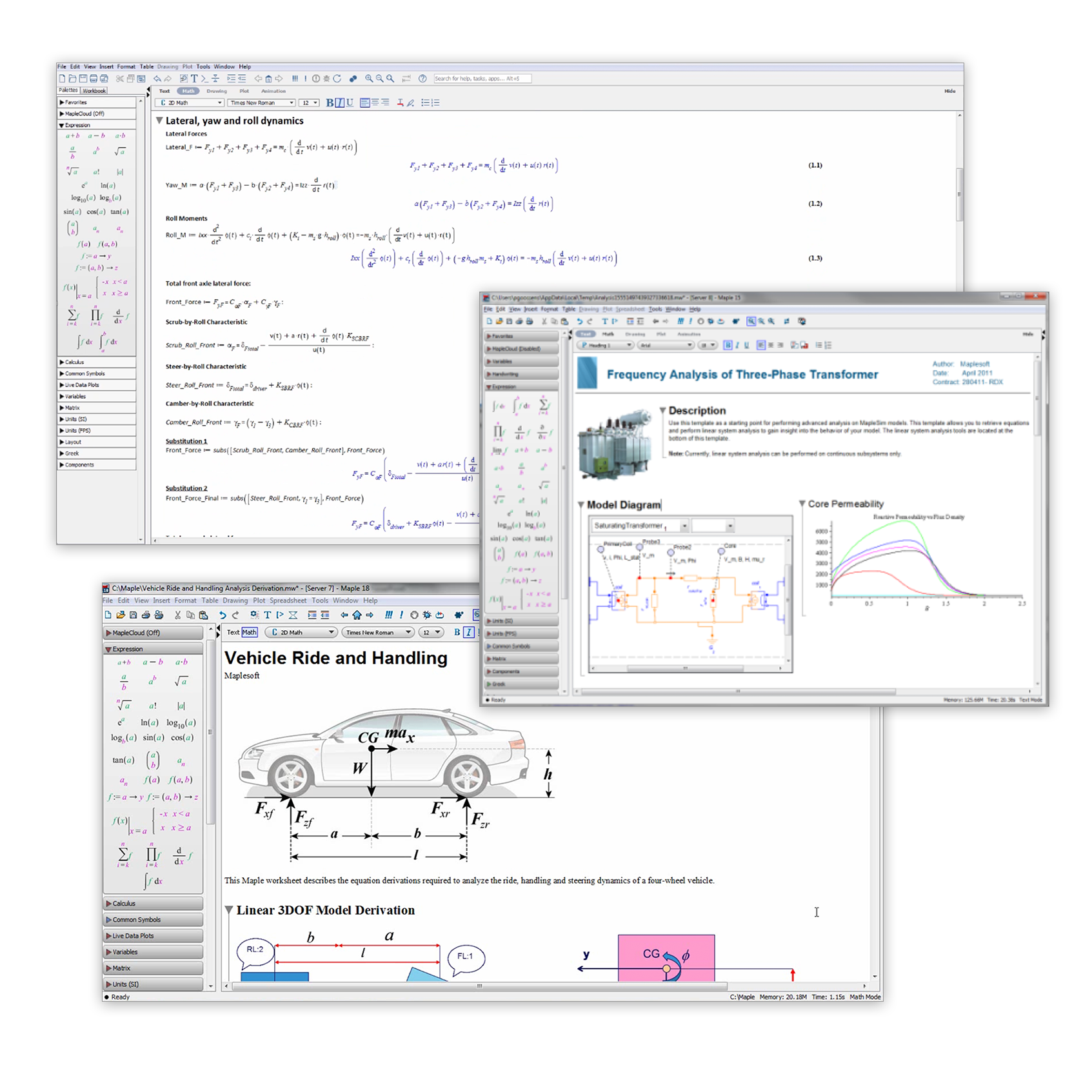 |
La base matemática de muchos proyectos de ingeniería suele elaborarse de forma desordenada, ya sea en papel o en una hoja de cálculo. Sin embargo, este enfoque informal conlleva riesgos. No solo pueden propagarse errores de cálculo a lo largo del proyecto, sino que también se corre el riesgo de perder las suposiciones, la información y los detalles de derivación necesarios para trabajos futuros. Con Maple, puede tratar sus cálculos como el valioso recurso que son.
|
- Detalles
- Categoría: Comsol
- Visto: 622
Las baterías de estado sólido (SSB, solid state batteries) representan la próxima generación del almacenamiento energético, ofreciendo mayor densidad de energía, tiempos de carga más rápidos y una seguridad superior en comparación con las baterías de ion-litio convencionales. Entre las ventajas destacadas, las SSB podrían alcanzar vidas útiles de 15-20 años y tiempos de carga de solo 3-12 minutos para alcanzar el 80 % de su capacidad, gracias a la eliminación del electrolito líquido y a su mayor integridad estructural.
La simulación es clave para entender y optimizar su comportamiento, permitiendo analizar el transporte iónico, las reacciones electroquímicas y las tensiones mecánicas dentro de un mismo entorno de modelado. En este sentido, COMSOL Multiphysics® se presenta con una herramienta con enorme potencial [1]. En el tutorial “Heterogeneous Model of a Solid-State Battery Unit Cell” [2], se presenta un modelo heterogéneo de una batería SSB en COMSOL Multiphysics®. El modelo de celda, cuya geometría se muestra en la Figura 1, incluye:
- Electrodo positivo compuesto: el material activo se aproxima mediante partículas esféricas, y un electrolito sólido rellena los espacios vacíos.
- Electrodo negativo de litio metálico.
- Separador de electrolito sólido entre el electrodo positivo y el negativo.
La Figura 2 muestra el entorno de modelización y simulación de este ejemplo de SSB en COMSOL Multiphyscis®. Los módulos recomendados para realizar este tipo de simulaciones son: Battery Design Module, CAD Import Module, Structural Mechanics Module, y Nonlinear Structural Materials Module.
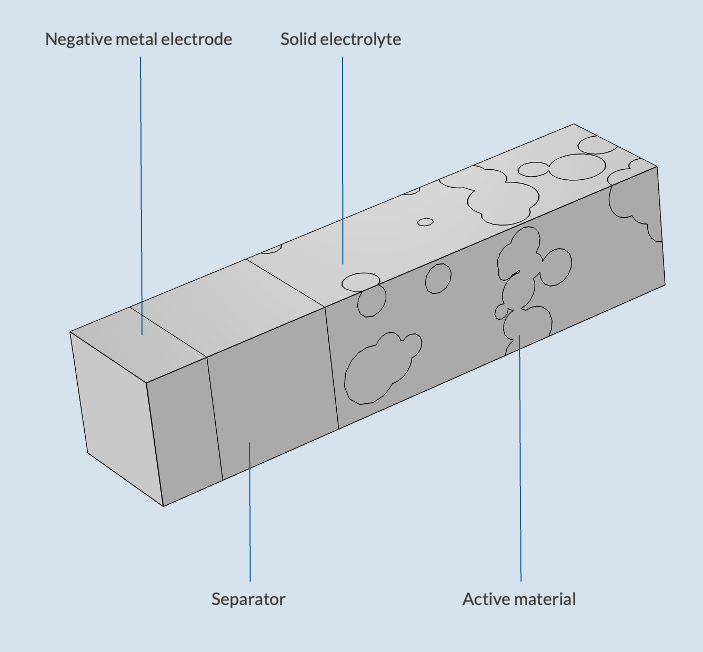
Figura 1. Geometría de la batería SSB modelizada en COMSOL Multiphysics®.
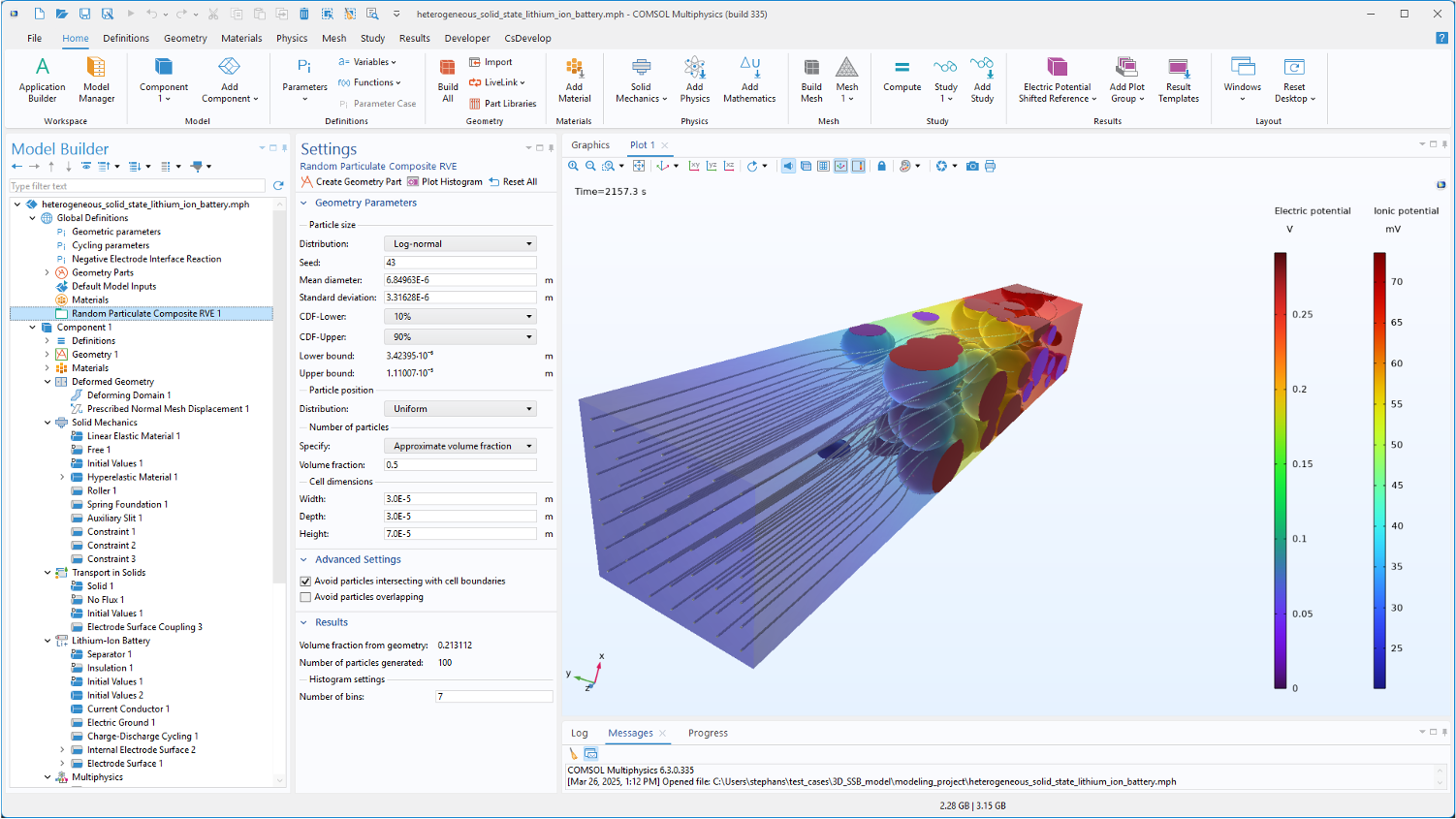
Figura 2. Entorno de simulación en COMSOL Multiphysics® para un modelo de SSB.
Referencias
[1] COMSOL Blog, Modeling a Solid-State Battery Cell in COMSOL Multiphysics® (2025).
[2] COMSOL Application Library: Heterogeneous Model of a Solid-State Battery Unit Cell
- Detalles
- Categoría: Minitab
- Visto: 524
Por Josué Zable.
Al diseñar un nuevo producto, incluso las variaciones más pequeñas pueden generar grandes problemas. Ya sea un conjunto de motor, la carcasa de un smartphone o un dispositivo médico, cada componente debe encajar con precisión para que el producto final funcione según lo previsto. Aquí es donde entra en juego el análisis de acumulación de tolerancias.
¿Qué es el análisis de acumulación de tolerancia?
El análisis de acumulación de tolerancias se utiliza para optimizar el diseño de productos para su ensamblaje. En efecto, se utiliza para calcular los efectos acumulativos de las tolerancias de las piezas en un ensamblaje. En general, la mayoría de los ingenieros comprenden la importancia de definir tolerancias optimizadas por pieza, pero pueden no considerar las tolerancias globales, especialmente en un entorno de ensamblaje y prueba. El análisis de acumulación de tolerancias ayuda a los ingenieros a predecir cómo se combinan las variaciones de las piezas en un ensamblaje y si el resultado final cumplirá con las especificaciones incluso antes de construir el primer prototipo.
Dos tipos de análisis de acumulación de tolerancias: el peor de los casos y el método Monte Carlo
Hay dos enfoques principales para el análisis de acumulación de tolerancia:
Análisis del peor caso posible: este enfoque asume que todas las tolerancias se encuentran en sus límites extremos en la misma dirección. Es simple y conservador, lo que garantiza el ajuste, pero a menudo conlleva ingeniería excesiva y costos innecesarios.
Análisis de Monte Carlo: Este enfoque utiliza distribuciones de probabilidad para modelar la variación en el mundo real. En lugar de asumir lo peor, simula miles de resultados de ensamblaje para estimar la probabilidad de fallo. Este enfoque refleja la realidad con mayor precisión y puede justificar tolerancias más flexibles (y más económicas), manteniendo el rendimiento.
Cómo realizar el apilamiento de tolerancias de Monte Carlo en Minitab
Con la herramienta de simulación de Monte Carlo de Minitab Workspace, los ingenieros pueden configurar rápidamente un modelo de tolerancia:
- Definir entradas: Ingrese las dimensiones de los componentes y sus tolerancias o distribuciones (normal, uniforme, etc.).
- Construya la ecuación: combine estas entradas para representar la dimensión general del ensamblaje.
- Ejecutar simulaciones: Minitab simula miles de combinaciones de ensamblajes.
- Interpretar resultados: ver la distribución de salida, la capacidad (Ppk/Cpk) y la probabilidad de cumplir con las especificaciones.
Construir mejores productos con diseño basado en datos
El análisis de acumulación de tolerancias acorta la distancia entre la intención de diseño y la realidad de fabricación. Al cuantificar la incertidumbre, los ingenieros toman decisiones informadas que equilibran el rendimiento, el coste y la viabilidad de fabricación. Si bien el análisis del peor caso posible puede ser más común y sigue siendo eficaz, la simulación de Monte Carlo proporcionará, en última instancia, un enfoque más realista, permitiendo tolerancias más flexibles y proporcionando un enfoque de diseño más práctico.
- Detalles
- Categoría: Comsol
- Visto: 672
En la Conferencia COMSOL 2025 de Ámsterdam, tendrá la oportunidad de ver cómo otros ingenieros e investigadores utilizan el modelado y la simulación en sus respectivos campos. Entre otras sesiones, los tres días de la conferencia incluirán dos sesiones con ponencias invitadas consecutivas, seleccionadas por el comité del programa a partir de las propuestas de Showcase Your Work.
Vea la lista de charlas invitadas a continuación:
SESIÓN 1
- "3D Microstructure-Resolved Modeling of Zinc–Air Batteries: Impact on Rechargeability and Performance", por Mahshid Moradi, Technical University of Berlin
- "Coupling Multiscale Phenomena in Alkaline Electrolyzer Stack Simulation Using Reduced-Order Models", por Kresten Juel Jensen, resolvent P/S
- "Analyzing the Interplay Between Strain, Temperature, and Optical Response in GeSn Microstructures", por Costanza Lucia Manganelli, IHP - Leibniz Institute for Innovative Microelectronics
- "Impact of the Key Aging Mechanisms in NMC Batteries and Their Consequences in Degradation", por Rashid Ahmed Rifat, BIC-MOBI, Vrije Universiteit Brussel
SESIÓN 2
- "How to Build a Digital Twin with a COMSOL App for Industrial Continuous Monitoring", por Giuseppe Petrone, BE CAE & Test
- "Simulation Apps at LEONI: Use Cases, Challenges, and Solutions Within a Global Company", por Michael Dauer, LEONI Bordnetz-Systeme GmbH
- "A New Licensing Tool for Compiled COMSOL Apps", por Daniel Ericsson, Deflexional AB
- "3ω-method in Production Flow for Thermal Flow Sensors", por Yuliia Tykhonenko-Polishchuk, Saxion University of Applied Sciences, LED, Applied Nanotechnology Research Group
SESIÓN 3
- "Innovative Product Design in EV Charging Connectors: Leveraging Topology and Shape Optimization", por Roman Obrist, Huber+Suhner AG
- "Modeling and Optimization of 3D Electroformed Ni Electrodes for Alkaline Electrolysis in COMSOL®", por Abimbola Ashaju, Veco B.V.
- "Lifetime Prediction of PEM Fuel Cells in Maritime Applications", por Binaya Baidar, ABB
- "3D Transient Simulation of a Planar SOFC: Bridging Microstructure and Multiphysics Models", por Mohamed El-Hachemi, Luxembourg Institute of Science and Technology
SESIÓN 4
- "Modeling Superconductor AC Losses in the STEP TF Magnet During Plasma Initiation", por P.C. Spruijtenburg, Demcon multiphysics
- "Evolution of a Geological Disposal Facility for Radioactive Waste in Domal Salt", por Jeroen Bartol, COVRA
- "Development and Utilization of Models for the Electrical Conditions in Submerged Arc Furnaces (SAF)", por Manuel Sparta, NORCE Research "Multiphysics Modeling of Electrohydrodynamic Drying — A Staggered Modeling Approach", por Zulhaj Rizki, Wageningen University
SESIÓN 5
- "Simulation and Validation of the Transfer Molding Process of a Large-Scale Power Semiconductor Module", por Cédric Kocher, University of Applied Sciences and Arts Northwestern Switzerland, Institute of Thermal and Fluid Engineering
- "Efficient Thermohydrodynamic Lubrication Modeling of Polymer Sliders Accounting for Cavitation", por Giorgos Kakolyris, Delft University of Technology
- "Computational Modeling of Lymph Node Flow, Cell Transport, and Tissue Mechanics", por Riana Priya Kandhai, University of the West Indies
- "Modeling the Dry Conversion Process with COMSOL Multiphysics®", por Patrick Namy, SIMTEC
SESIÓN 6
- "Surrogate Modeling-Based Optimization in Horology", por Gaétan Simonnot, HEPIA, University of Applied Sciences and Arts Western Switzerland
- "Synchrotron X-Ray and FE Modeling of Flax Yarns for Technical Textile Applications", por Sofiane Guessasma, INRAE
- "Modeling of the Molten Metal Hydrodynamics in Vacuum Arc Cathode Spots Using the Level Set Method", por Anamaria Spataru, Siemens Energy
- "Boosting the Actuator Efficiency of Reluctance Actuators with Permanent Magnets", por Mariёlle Meijer, Demcon high-tech systems
- Detalles
- Categoría: Lakes
- Visto: 398
Existen muchas razones por las que puede ser necesario crear una copia de un proyecto de modelado. Quizás se desee modificar un escenario sin sobrescribir los resultados anteriores, o se necesite volver a ejecutar el proyecto con un conjunto diferente de datos meteorológicos, manteniendo el resto de las entradas.
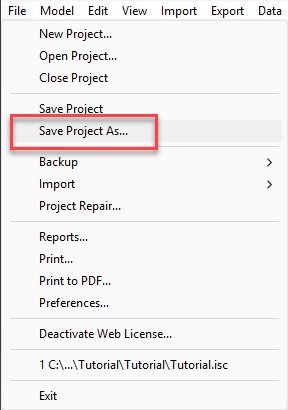
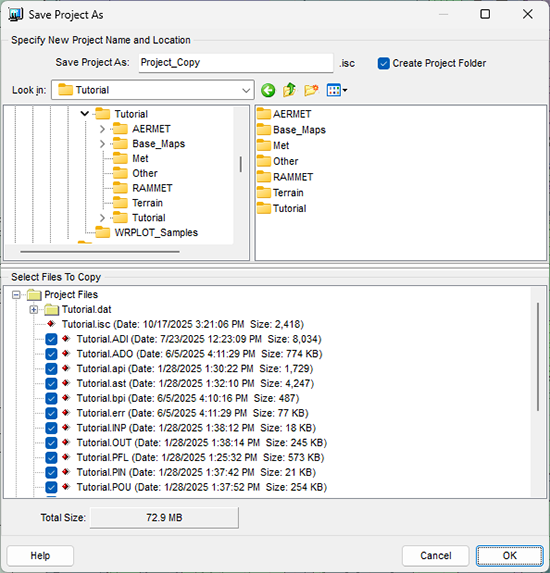
- Guardar proyecto como: especifique el nombre del nuevo proyecto.
- Buscar en: Seleccione la carpeta donde desea guardar el proyecto copiado. Puede ser el mismo directorio que el proyecto original o cualquier otra ubicación del equipo.
- Crear carpeta de proyecto: Guarde el proyecto en una subcarpeta independiente. Desmarcar esta opción guardará los archivos del proyecto copiados directamente en el directorio seleccionado, pero puede dificultar la gestión de archivos.
- Seleccionar archivos para copiar: Elija los archivos del proyecto original que desee conservar. Puede optar por no copiar archivos muy grandes para ahorrar tiempo y espacio.
- Detalles
- Categoría: Minitab
- Visto: 460
Por Adam Russell y Brittany Clinton
.A medida que la fabricación de procesos se automatiza y se integra digitalmente, el volumen y la complejidad de los datos de proceso se han disparado. Los sensores registran miles de variables en tiempo real. Las métricas se rastrean en turnos, lotes y máquinas. Los métodos estadísticos tradicionales, aunque siguen siendo valiosos, a veces no logran gestionar la magnitud, la complejidad y los matices de estos datos.
Aquí es donde entra en juego el aprendizaje automático (ML), y el análisis predictivo de Minitab puede ayudarle. En resumen, el ML permite a los fabricantes descubrir patrones, predecir resultados y optimizar el rendimiento de maneras que antes no eran posibles. A diferencia de la regresión clásica, el ML no requiere suposiciones estrictas sobre la estructura de los datos. Aprende directamente de ejemplos reales, gestionando la multicolinealidad, los efectos rezagados, el comportamiento no lineal y más.
En el modelado clásico, el objetivo es definir relaciones matemáticas entre las variables de entrada (X) y las variables de salida (Y). Sin embargo, en muchos procesos, la función subyacente es demasiado compleja o desconocida. El aprendizaje automático no intenta adivinar la fórmula. Aprende patrones directamente de los datos, utilizando ejemplos uno tras otro para construir un modelo que predice Y al dar nuevos valores de X. Esto lo hace ideal para entornos de fabricación, donde los procesos son complejos y las interacciones entre variables son difíciles de definir. El aprendizaje automático aprende sin necesidad de que un humano predefina las reglas.
A continuación, se presentan seis trampas comunes en el análisis de datos que la suite de Análisis Predictivo de Minitab puede combatir. Recomendamos a todos los profesionales con nivel Black Belt y Master Black Belt que se familiaricen plenamente con las técnicas de regresión múltiple antes de utilizar el aprendizaje automático. Nuestro objetivo es ayudar a los profesionales a condensar el número de variables de entrada plausibles a las mínimas significativas para su posterior exploración mediante el Diseño de Experimentos, un método ampliamente compatible con Minitab.
Las seis trampas
Trampa n.° 1: Datos sucios
Los datos históricos pueden estar contaminados con valores extremos, valores atípicos y valores faltantes. Estos problemas dificultan la estimación fiable de coeficientes de ecuaciones de regresión.
- Valores extremos: un valor único, Xi, puede estar alejado del resto de los datos; si este es el caso, Xi puede ejercer una gran influencia en la estimación de regresiones.
- Valores atípicos: Xi puede no estar muy lejos de los otros valores X, pero el residuo del modelo (real - predicción) puede ser grande y mayor que 3 desviaciones estándar, suponiendo que los residuos se distribuyen normalmente con un promedio general = 0.
- Valores faltantes: en la regresión por pasos y de mejores subconjuntos, se eliminarán filas enteras de datos si algún predictor elegido (X) tiene un valor faltante en la fila.
Trampa n.° 2: Big Data
El tamaño de los datos está relacionado con el número de filas y el número de columnas.
- Si el número de predictores (p) es grande en relación con el número de observaciones (n), entonces esto se vuelve muy complejo, o incluso computacionalmente imposible, para la regresión clásica.
- En la regresión clásica, n debe ser mayor que p para estimar el error del modelo y calcular los valores p de cada predictor. Si no se estima el error del modelo, no existe un valor de r-cuadrado.
- Sin r-cuadrado y residuos, no podemos saber si la ecuación de regresión modela bien los datos.
Trampa n.° 3: Multicolinealidad
Cuando las entradas (X) están correlacionadas (son dependientes) entre sí, los coeficientes de correlación entre dos predictores superiores a 0,5 indican un problema.
- La ventana de sesión de regresión clásica proporciona información sobre la multicolinealidad.
- Factor de Inflación de la Varianza (FIV): mide cuánto aumenta la varianza de un coeficiente de regresión estimado si los predictores están correlacionados. FIV = 1 / (1 – r² ). Si FIV > 5, esto podría representar un problema grave para el modelo.
- R-cuadrado y R-cuadrado (ajustado): Añadir predictores correlacionados en un modelo de regresión clásica provoca la divergencia de estos valores. El R-cuadrado (ajustado) impide al modelador incluir predictores correlacionados con otros predictores ya presentes en el modelo.
Trampa n.° 4: Interacciones
Cuando la influencia de un predictor (X1) depende de la configuración de un segundo predictor independiente (X2).
- Las interacciones aumentan los términos del modelo: matemáticamente, el número de interacciones aumenta exponencialmente con el número de predictores. Las interacciones pueden ser bidireccionales, tridireccionales, cuádruples, etc. En la práctica, las interacciones bidireccionales son frecuentes, pero las interacciones de orden superior son poco frecuentes.
- Interacciones globales vs. locales: La regresión clásica obliga a que las interacciones sean globales; si se descubre que una interacción es significativa, debe ocurrir por igual en todas las dimensiones del espacio predictor. Las interacciones localizadas pueden ocurrir en la industria, pero son difíciles de modelar con la regresión clásica.
Trampa n.° 5: No linealidad
La regresión clásica es lineal por diseño. La expresión común de regresión lineal es Y = mx + b. Esta fórmula básica puede extenderse a otros tipos de ecuaciones lineales. Por ejemplo, X2 es una función lineal. Sin embargo, 2X no lo es. Para que una función sea lineal, debe serlo en sus exponentes.
Las funciones no lineales no se pueden modelar mediante regresión simple, regresión por pasos o regresión por mejores subconjuntos. Si se espera no linealidad, el usuario debe proporcionar la relación no lineal subyacente o elegir entre varias alternativas.
El aprendizaje automático asume que todas las relaciones X-Y son no lineales. Esta suposición significa que incluso las funciones lineales pueden modelarse de forma sencilla con algoritmos de aprendizaje automático. El usuario no necesita conocer la función no lineal adecuada para continuar con el aprendizaje automático.
Trampa n.° 6: Efectos retardados
En el análisis de datos de fabricación de procesos continuos, el analista debe crear o desplazar con frecuencia cada predictor (X) hacia adelante en el tiempo para que coincida con la respuesta esperada (Y). Si bien la regresión clásica también puede gestionar los efectos rezagados, los modelos de aprendizaje automático suelen ser más eficaces a la hora de incorporarlos.
Por ejemplo, un proceso químico tiene un predictor importante (X) de una variable de respuesta (Y). El tiempo de residencia nominal del proceso es de 4 horas. Si el operador modifica X, la variable de respuesta (Y) cambia 4 horas después del cambio en X. Por supuesto, este sencillo ejemplo implica ciertas suposiciones importantes. En ocasiones, los procesos de flujo pistón no son exactamente de flujo pistón y la retromezcla influye. En ocasiones, el efecto del cambio en X se extiende en el tiempo en comparación con la respuesta en Y. En estas situaciones, es necesario evaluar múltiples desplazamientos temporales del predictor (X).
De las trampas a la transformación
Los métodos tradicionales siguen siendo valiosos, pero no siempre están diseñados para la escala y la complejidad de los datos de fabricación de procesos modernos. El aprendizaje automático en el análisis predictivo de Minitab ayuda a superar estos desafíos al gestionar automáticamente la no linealidad, los efectos retardados y las variables complejas del mundo real. Con él, puede ir más allá del simple análisis de datos para predecir resultados, prevenir fallos y optimizar el rendimiento con confianza.