- Detalles
- Categoría: NAG
- Visto: 1657
Introducción
El aprendizaje automático (ML) está transformando la forma en que resolvemos problemas, analizamos datos y tomamos decisiones. Pero para liberar todo su potencial, las técnicas de optimización desempeñan un papel fundamental. Esta guía explora cómo la optimización se relaciona con el aprendizaje automático para crear sistemas más inteligentes, rápidos y eficientes, que resuelvan desafíos complejos del mundo real en sectores como las finanzas, la logística y la atención sanitaria.
Antes de profundizar en el tema, aclaremos los conceptos básicos.
¿Qué es el aprendizaje automático (ML)?
El aprendizaje automático es un sistema de inteligencia artificial que permite a los ordenadores aprender de los datos y hacer predicciones o tomar decisiones sin estar programadas explícitamente.
- Programación tradicional: seguir instrucciones fijas y predefinidas.
- Aprendizaje automático: aprenda patrones a partir de datos y mejore el rendimiento a lo largo del tiempo.
Cómo funciona
- Alimente el modelo con datos.
- El modelo analiza los datos, identifica patrones y genera información.
- A medida que el modelo procesa más datos, ajusta y mejora sus predicciones.

Principales tipos de aprendizaje automático
El aprendizaje automático se clasifica normalmente en tres tipos:
Aprendizaje supervisado
Definición: Los modelos aprenden de datos etiquetados (datos con respuestas correctas).
Ejemplos:
- Regresión: predice valores continuos (por ejemplo, precios de la vivienda).
- Clasificación: predice categorías (por ejemplo, spam vs. no spam).
2. Aprendizaje no supervisado
Definición: Los modelos analizan datos no etiquetados para encontrar patrones ocultos.
Ejemplo:
- Agrupamiento: Agrupar clientes según su comportamiento de compra.
3. Aprendizaje por refuerzo
Definición: Los modelos aprenden interactuando con un entorno y recibiendo recompensas o penalizaciones por sus acciones. Ejemplo:
- Entrenar robots para caminar u optimizar el uso energético del hogar.
¿Por qué es importante el aprendizaje automático?
El aprendizaje automático está transformando las industrias al mejorar la eficiencia, la toma de decisiones y la resolución de problemas. A continuación, se ofrecen algunos ejemplos:
- Fabricación: Predecir fallas de máquinas para permitir el mantenimiento preventivo y reducir costos.
- Finanzas: Detecte transacciones fraudulentas en tiempo real y personalice servicios financieros, como préstamos a medida.
- Logística: Optimice las rutas de entrega para ahorrar tiempo y combustible.
Atención médica: analizar datos médicos para ayudar con diagnósticos tempranos y planes de tratamiento personalizados.
¿Qué son las técnicas de optimización?
Las técnicas de optimización son métodos matemáticos que se utilizan para mejorar los modelos de aprendizaje automático. Buscan la mejor solución posible a un problema, a menudo minimizando los errores (funciones de pérdida) o maximizando el rendimiento (precisión).
Técnicas de optimización habituales
1. Descenso de gradiente
- Qué hace: ajusta los parámetros de un modelo paso a paso para minimizar los errores.
- Por qué es importante: es la columna vertebral del entrenamiento de la mayoría de los modelos de ML, ya que garantiza que los modelos converjan en la solución óptima.
2. Recocido simulado
- Cómo funciona: se inspira en el enfriamiento de metales. Explora soluciones, incluidas algunas menos óptimas inicialmente, para evitar quedarse estancado en una “mejor” solución local.
- Ideal para: problemas complejos con espacios de soluciones impredecibles (por ejemplo, programación, optimización de rutas).
3. Optimización bayesiana
- Qué hace: utiliza probabilidades para predecir la calidad de las soluciones antes de probarlas.
- Beneficio clave: ideal para ajustar hiperparámetros, ahorrando tiempo y recursos computacionales significativos.
4. Algoritmos genéticos
- Cómo funciona: Imita la selección natural:
- Comience con múltiples soluciones.
- Seleccione lo mejor.
- Combínalos (cruzalos) y modifícalos (muta) para mejorar los resultados.
- Ideal para: problemas con múltiples respuestas posibles, como optimización del diseño y programación.
5. Adagrado
- Qué hace: ajusta las tasas de aprendizaje individualmente para cada parámetro en función de gradientes anteriores.
- Por qué es útil: Perfecto para manejar datos dispersos (por ejemplo, procesamiento de texto o imágenes), ya que se centra en características menos frecuentes para un mejor aprendizaje.
Ahora que hemos sentado las bases para el aprendizaje automático y la optimización, profundicemos más. En las siguientes secciones, exploraremos cómo las técnicas de optimización potencian el rendimiento del aprendizaje automático, abordan desafíos del mundo real y crean valor tangible en todas las industrias.
Fundamentos de optimización matemática
¿Qué es la optimización matemática?
En esencia, la optimización matemática es el proceso de encontrar la mejor solución posible para un problema determinado en un conjunto definido de condiciones o restricciones. Esto implica:
- Maximizar o minimizar una función objetivo: una fórmula matemática que representa el objetivo (por ejemplo, minimizar el costo, maximizar la precisión).
- Satisfacer restricciones: reglas que restringen las posibles soluciones (por ejemplo, recursos o tiempo limitados).
Expresión matemática
Optimiza: f(x) sujeto a las restricciones g(x) ≤ c
Dónde:
f(x): Función objetivo a maximizar o minimizar.
g(x): Restricciones limitantes de x.
c: Límites de las restricciones.
Por ejemplo, en ML, f(x) podría representar la función de pérdida (tasa de error) y el objetivo es minimizarla durante el entrenamiento del modelo.
Principales aplicaciones del aprendizaje automático
La optimización matemática proporciona la base para muchos procesos críticos en el aprendizaje automático. Analicemos sus principales aplicaciones:
1. Modelos de entrenamiento: minimización de funciones de pérdida
- Qué significa: Durante el entrenamiento, los modelos de ML tienen como objetivo minimizar una función de pérdida, que cuantifica qué tan lejos están las predicciones de los valores reales. Los algoritmos de optimización ajustan los parámetros (por ejemplo, pesos y sesgos) para reducir este error paso a paso.
- Ejemplo: una red neuronal que predice los precios de la vivienda utiliza la optimización para minimizar la diferencia entre los precios previstos y los reales.
2. Ajuste de hiperparámetros: búsqueda de configuraciones óptimas
- Qué significa: Los hiperparámetros son configuraciones (por ejemplo, tasa de aprendizaje, tamaño de lote) que controlan cómo aprenden los modelos de ML. Las técnicas de optimización ayudan a encontrar los mejores hiperparámetros para maximizar el rendimiento.
- Por qué es fundamental: Las configuraciones de hiperparámetros deficientes pueden generar modelos que se sobreajusten, se desajustan o se entrenan demasiado lentamente.
- Ejemplo: la optimización bayesiana predice la mejor combinación de hiperparámetros para reducir el gasto computacional y aumentar la precisión del modelo.
3. Asignación de recursos: garantizar la eficiencia computacional
- Qué significa: Los modelos de ML suelen requerir recursos importantes, como memoria y tiempo de GPU. La optimización garantiza que los recursos se asignen de manera eficiente para equilibrar los costos y el rendimiento.
- Ejemplo: Los sistemas de aprendizaje automático distribuido optimizan el uso de recursos en varias GPU para reducir el tiempo de entrenamiento y, al mismo tiempo, respetar los límites de costos. Las plataformas en la nube asignan dinámicamente los recursos del servidor para equilibrar las cargas y ahorrar energía.
Perspectiva más amplia
Si bien el aprendizaje automático aprovecha en gran medida la optimización, es importante reconocer que la optimización matemática es un marco universal. Más allá del aprendizaje automático, se utiliza para:
- Optimizar rutas de entrega en logística.
- Asignar recursos para carteras financieras.
- Agilizar los cronogramas de producción en la industria manufacturera.
Esta versatilidad hace que la optimización sea una herramienta indispensable en todas las industrias, permitiendo una toma de decisiones más inteligente y una mayor eficiencia.
Uniéndolo todo
La optimización matemática proporciona la columna vertebral teórica para muchas tareas de aprendizaje automático, desde la minimización de funciones de pérdida hasta la asignación eficiente de recursos. Comprender estos fundamentos es crucial para liberar todo el potencial de los modelos de aprendizaje automático para resolver problemas del mundo real.
La intersección de la optimización y la IA/ML
La optimización matemática y el aprendizaje automático (ML) no solo coexisten, sino que se impulsan mutuamente. La optimización funciona como el motor que impulsa la eficiencia y la eficacia del ML, lo que permite algoritmos más inteligentes, decisiones más rápidas y mejores resultados en todas las industrias. Analicemos esto.
Cómo las técnicas de optimización potencian el aprendizaje automático
1. Eficiencia del entrenamiento
- Qué significa: La optimización es la columna vertebral del entrenamiento de los modelos de ML. Al minimizar la función de pérdida, ayuda a que los algoritmos aprendan más rápido y con menos recursos computacionales.
- Ejemplo: Gradient Descent y sus variantes (por ejemplo, Adam, RMSProp) refinan iterativamente los parámetros del modelo, garantizando que los modelos converjan a la mejor solución de manera eficiente.
- Por qué es importante: Una convergencia más rápida significa menor tiempo de entrenamiento, menores costos computacionales y una implementación más rápida de soluciones de ML.
2. Modelos de toma de decisiones
- Qué significa: La optimización permite que los modelos de ML tomen decisiones maximizando o minimizando objetivos específicos bajo restricciones.
Aplicaciones
- Precios dinámicos: los modelos de optimización ayudan a las empresas a establecer precios en tiempo real, equilibrando la oferta, la demanda y los márgenes de ganancia.
- Gestión de cartera: Los algoritmos optimizan la asignación de activos, teniendo en cuenta el riesgo y la rentabilidad.
- Ejemplo: Netflix utiliza sistemas de recomendación basados en optimización para determinar el mejor contenido para sugerir a usuarios individuales.
3. Aprendizaje por refuerzo
- Qué significa: El aprendizaje de refuerzo (RL) aprovecha la optimización para permitir que los agentes aprendan estrategias óptimas maximizando las recompensas acumuladas a lo largo del tiempo.
- Cómo funciona: Los problemas de RL se enmarcan como procesos de decisión de Markov (MDP), donde la optimización determina las mejores acciones que un agente debe tomar en un estado determinado.
- Ejemplo: Los vehículos autónomos utilizan RL para optimizar las estrategias de conducción, equilibrando la velocidad, la seguridad y la eficiencia del combustible.
- Por qué es importante: sin optimización, los agentes de RL tendrían dificultades para identificar políticas efectivas en entornos complejos de varios pasos.
Estudio de caso: Cómo el aprendizaje automático redujo los costos y aceleró los resultados
Aviso legal. Este escenario ficticio ilustra el potencial transformador del aprendizaje automático (ML) en la logística. Está diseñado con fines educativos y no se basa en un relato real.
SwiftRoute estaba perdiendo dinero, perdiendo tiempo y frustrando a los clientes. Las rutas de entrega ineficientes, los costos de combustible en aumento y los plazos incumplidos estaban hundiendo sus ganancias y la satisfacción de los clientes.
- Rutas ineficientes: los conductores tardaron un 20% más en completar las entregas que sus competidores.
- Costes en aumento: el consumo de combustible y el mantenimiento del vehículo reducen profundamente los márgenes de ganancia.
- Plazos incumplidos: las tasas de entrega a tiempo cayeron por debajo del 75 %, lo que generó enojo y pérdida de clientes.
Ante la creciente competencia y la reducción de los márgenes, SwiftRoute necesitaba una solución para recuperar el control y reconstruir la confianza.
La solución: logística impulsada por ML
SwiftRoute adoptó un enfoque de aprendizaje automático para optimizar las operaciones:
Limpieza de datos:
- Años consolidados de datos confusos de GPS, entregas y flotas.
- Se eliminaron duplicados y errores para crear un conjunto de datos confiable para el análisis.
Desarrollo de modelos ML:
- Desarrollé modelos predictivos para ajustar dinámicamente las rutas de entrega en tiempo real según el tráfico, el clima y las cargas de paquetes.
- Programación lineal aplicada y aprendizaje de refuerzo para la optimización de rutas.
Prueba piloto:
- Implementamos la solución ML con una pequeña flota para identificar debilidades y ajustar el sistema.
Implementación en toda la empresa:
- Se adaptó la solución a toda la flota y se capacitó a los conductores utilizando herramientas gamificadas para garantizar la aceptación y una adopción sin problemas.
Los resultados: victorias tangibles
SwiftRoute transformó sus operaciones logísticas y logró un éxito medible:
- Entregas más rápidas: los tiempos promedio de ruta disminuyeron considerablemente.
- Ahorros: La reducción del consumo de combustible y la optimización del uso del vehículo dieron como resultado una disminución de gastos.
- Satisfacción del cliente mejorada: entregas puntuales mejoradas.
- Ahorros operativos totales: ganancias de eficiencia en todos los ámbitos.
Los obstáculos y cómo los superaron
El viaje de SwiftRoute no estuvo exento de desafíos, pero las acciones estratégicas los ayudaron a superar los obstáculos:
Datos desordenados: se invirtió tiempo y esfuerzo en limpiar y estandarizar años de datos inconsistentes.
Resistencia del conductor: Los programas de capacitación gamificados incentivaron a los conductores a adoptar el nuevo sistema y brindaron apoyo continuo.
Refinamiento del modelo: las actualizaciones iterativas mejoraron la capacidad del modelo para manejar datos meteorológicos y de tráfico en tiempo real.
Conclusiones para los investigadores de operaciones
El éxito de SwiftRoute ofrece información útil:
Comience poco a poco: realice pruebas piloto para validar las soluciones de ML antes de ampliarlas a otras operaciones.
Priorizar la calidad de los datos: unos datos limpios y confiables son la base de cualquier iniciativa de aprendizaje automático exitosa.
Invertir en la capacitación del equipo: involucre a las partes interesadas desde el principio para garantizar la adopción y el éxito a largo plazo.
Mida los KPI sin descanso: realice un seguimiento de las métricas clave (por ejemplo, tiempo de entrega, ahorro de costos, satisfacción del cliente) para demostrar el ROI y perfeccionar la solución.
- Detalles
- Categoría: Comsol
- Visto: 1827
La actualización Update 1 de la versión 6.3 del software COMSOL® (compilación 6.3.0.335) proporciona mejoras de rendimiento y estabilidad para COMSOL Multiphysics®, COMSOL Server™, COMSOL Client para su uso con COMSOL Server™ y Model Manager Server.
La actualización se aplica a la versión 6.3 del software COMSOL® (compilación 6.3.0.290).
A continuación listamos algunas mejoras introducidas en la actualización:
COMSOL Multiphysics
- La ventana Chatbot ahora admite la funcionalidad de Azure OpenAI Service.
- Mejoras significativas en la funcionalidad de limpieza de geometría y la operación virtual de fusión de caras.
- Se solucionó un problema que provocaba que apareciera texto negro sobre un fondo negro al editar celdas de una tabla mientras se usaba una combinación de tema oscuro en COMSOL Multiphysics® y tema oscuro de alto contraste en Windows®.
- Las funciones externas ahora producen un error cuando sus nombres entran en conflicto con los nombres reservados.
- Se resolvió un problema por el cual COMSOL Multiphysics® dejaba de responder al evaluar un conmutador de función que contenía una rama de función que dependía de una función global o local definida por el usuario con la misma etiqueta de nodo que la rama.
- En las interfaces de malla móvil y geometría deformada, las expresiones que definen el desplazamiento de la malla en un nodo de deformación prescrita ahora se evalúan directamente en los límites cuando se utilizan las coordenadas de los límites. Este cambio puede producir resultados diferentes en comparación con las versiones anteriores si las expresiones involucran variables que son discontinuas entre el límite y los dominios adyacentes. Anteriormente, el desplazamiento del límite se determinaba promediando las expresiones evaluadas en los dominios adyacentes.
- Para mejorar el rendimiento al utilizar casos de carga, el resolvedor paramétrico ahora utiliza la opción Automático para el orden de ejecución del valor de parámetro . Si esto genera un comportamiento inesperado, es posible utilizar el valor predeterminado anterior Según lo especificado .
- Las variables dependientes de la salida para los modelos de orden reducido ahora almacenan consistentemente los valores correctos, independientemente del orden en que se enumeran las salidas en el nodo de reducción del modelo.
- Para los modelos de orden reducido con salidas lineales y retroalimentación de entrada, el vector de sesgo de salida ahora se calcula correctamente cuando las entradas tienen valores de entrenamiento distintos de cero.
- Los operadores de vibración aleatoria ahora son compatibles con la opción de cálculo de flujo de contorno en la sección Discretización de la ventana Configuración para las interfaces de mecánica estructural relevantes. Esta opción está disponible cuando se habilita la configuración Opciones de física avanzadas .
- La interfaz de usuario para el paso de estudio de reducción del modelo se ha simplificado para el método de descomposición ortogonal (POD) adecuado.
- Se ha mejorado el mapeo de objetos de solución con datos adicionales, como soluciones anteriores y vectores propios izquierdos, para lograr una mayor solidez. Sin embargo, los objetos de solución antiguos aún pueden contener datos corruptos y causar errores internos cuando se utilizan. En tales casos, se recomienda volver a calcular la solución.
- Se ha mejorado el rendimiento de las animaciones de cámara.
- Se corrigió un error que impedía el uso de la Actualización de la biblioteca de aplicaciones en Linux ® con libwebkit2gtk-4.1 o superior, por ejemplo, en Ubuntu ® 24.04.
- La herramienta de administración de licencias lmadmin se ha eliminado del conjunto de instalación debido a vulnerabilidades de seguridad.
- Mejoras de seguridad, rendimiento, usabilidad y estabilidad.
Application Builder
- Se resolvió un problema en el que las secciones de la cinta en las aplicaciones aparecían habilitadas a pesar de estar inicialmente deshabilitadas.
- Se corrigió un error que podía impedir la apertura de archivos de modelos compilados para Java.
- Mejora del rendimiento del editor de formularios para aplicaciones con una gran cantidad de formularios.
- Mejoras de estabilidad.
Model Manager
- Mejoras de estabilidad.
Model Manager Server
Se solucionó un problema con el lanzamiento de un servidor Model Manager en sistemas Linux ® con kernels de tamaño de página grande, como Ubuntu® arm64+largemem. Un servidor de Model Manager ahora escribe un mensaje de error en la línea de comando y en el archivo de registro si el servidor no puede iniciarse debido a que un puerto ya está ocupado. La fecha mostrada en la interfaz web para un atributo primitivo del tipo de valor Fecha ya no depende de la zona horaria local del usuario. Mejoras de estabilidad.AC/DC Module
- Mejoras de estabilidad.
Acoustics Module
- Mejoras de estabilidad.
Battery Design Module
- Mejoras de estabilidad.
CAD Import Module
- Se agregó soporte para importar archivos ACIS® 2025 1.0 y SOLIDWORKS ® 2025 en Windows® y Linux®.
- Mejoras de estabilidad.
CFD Module
- Las nuevas configuraciones predeterminadas del resolvedor para simulaciones de flujo de fluidos estacionarios brindan reducciones sustanciales del tiempo de solución en la mayoría de los casos. Las nuevas configuraciones se aplican a la secuencia del resolvedor cuando se agrega un estudio estacionario o un paso de estudio estacionario , cuando las configuraciones del resolvedor se restablecen a sus valores predeterminados y a los estudios estacionarios existentes para los cuales no se ha editado el nodo Configuraciones del resolvedor.
- Mejoras de estabilidad.
Chemical Reaction Engineering Module
- Las advertencias de varias funciones de acoplamiento ahora solo se muestran cuando se resuelven las ecuaciones afectadas.
- Ahora se muestra una advertencia cuando las ecuaciones de transporte de masa en forma no conservativa se acoplan con un flujo de fluido compresible para las funciones de acoplamiento Flujo de reacción, Especies diluidas y Precipitación en flujo de fluido .
- Mejoras de estabilidad.
Composite Materials Module
- Mejoras de estabilidad.
Corrosion Module
- Mejoras de estabilidad.
Design Module
- Mejoras de estabilidad.
ECAD Import Module
- Mejoras de estabilidad.
Electric Discharge Module
- Definiciones de variables mejoradas para la emisión de electrones de campo de la función Electrodo en la interfaz de Descarga eléctrica.
- Mejoras de estabilidad.
Electrochemistry Module
- Mejoras de estabilidad.
Geomechanics Module
- Mejoras de estabilidad.
Heat Transfer Module
- Mejoras de estabilidad.
LiveLink™ for Inventor®
- Mejoras de estabilidad.
LiveLink™ for MATLAB®
- Mejoras de estabilidad.
LiveLink™ for Revit®
- Mejoras de estabilidad.
Metal Processing Module
- Mejoras de estabilidad.
Nonlinear Structual Materials Module
- Mejoras de estabilidad.
Optimization Module
- Mejoras de rendimiento para funciones de control y optimizaciones transitorias.
- Mejoras de estabilidad.
Pipe Flow Module
- Mejoras de estabilidad.
RF Module
- Mejoras de estabilidad.
Rotordynamics Module
- Mejoras de estabilidad.
Semiconductor Module
- Se corrigió un error en el que aparecía una advertencia falsa para el modelo de tunelaje WKB .
Structural Mechanics Module
- Se corrigió un error de falta de memoria que podía ocurrir cuando una interfaz de Layered Shell y una función de contacto estaban presentes simultáneamente.
- Se solucionó un problema con la generación automática de pruebas de materiales desde el nodo Material de prueba cuando una interfaz de Mecánica de sólidos o un subnodo Modelo de material usa selecciones de dominio manuales.
- Mejoras de estabilidad.
Uncertainty Quantification Module
- Mejoras de estabilidad.
Wave Optics Module
- Mejoras de estabilidad.
ACIS es una marca registrada de Spatial Corporation. Autodesk, el logotipo de Autodesk, Inventor y Revit son marcas registradas o marcas comerciales de Autodesk, Inc. y/o sus subsidiarias y/o afiliadas en los EE. UU. y/o en otros países. Linux es una marca registrada de Linus Torvalds en los EE. UU. y en otros países. macOS es una marca registrada de Apple Inc. en los EE. UU. y en otros países. MATLAB y Simulink son marcas registradas de The MathWorks, Inc. Microsoft, Excel y Windows son marcas registradas o marcas comerciales de Microsoft Corporation en los Estados Unidos y/o en otros países. SOLIDWORKS es una marca registrada de Dassault Systèmes. SolidWorks Corp. Ubuntu es una marca registrada de Canonical Ltd.
- Detalles
- Categoría: Minitab
- Visto: 1474
Por Oliver Franz
Existen muchas similitudes entre los procesos de construcción, los proyectos y los rompecabezas; cuando un elemento falla o una pieza no encaja, la finalización de todo el proyecto se ve afectada. A menudo, aparecen ineficiencias ocultas que reducen el presupuesto, amplían los plazos e incluso reducen la calidad.
Su trabajo como profesional de la mejora continua consiste en proteger los plazos, conservar el presupuesto y, lo más importante, mantener seguros a su equipo y a sus integrantes, lo cual no es una tarea fácil. La buena noticia es que estos desafíos no son insuperables y, con la información adecuada y las estrategias basadas en datos, puede perfeccionar sus procesos de manera eficiente.
Analicemos tres ineficiencias comunes y exploremos cómo solucionarlas con Minitab.
1. Los flujos de trabajo no optimizados provocan retrasos y cuellos de botella
Debido a la complejidad de los proyectos de construcción (hay muchos equipos, tareas y cronogramas involucrados), a menudo se producen cuellos de botella y demoras. Los equipos pueden estar esperando materiales, equipos o aprobaciones, mientras que las tareas mal secuenciadas interrumpen la productividad. Estas ineficiencias pueden generar pérdida de tiempo e incumplimiento de plazos, mayores costos de mano de obra y equipos, y frustración/insatisfacción entre los trabajadores y las partes interesadas externas, incluidos los clientes.
Con Minitab, puede mejorar sus proyectos de mejora continua con un conjunto completo de herramientas de mejora continua, como el mapeo del flujo de valor y el análisis de procesos para identificar los puntos débiles en los flujos de trabajo. Los equipos cuentan con herramientas estadísticas y de visualización de datos para identificar y abordar los retrasos. Por ejemplo, los diagramas de Pareto pueden destacar las causas más importantes de los cuellos de botella, mientras que el análisis de la capacidad del proceso garantiza que los flujos de trabajo alcancen los niveles de rendimiento deseados.
2. La repetición del trabajo debido a problemas de calidad aumenta los costos
Los defectos y errores en la construcción, ya sea en carreteras, edificios comerciales, residenciales o industriales, son más comunes de lo que probablemente nos gustaría. El problema principal es que muchas empresas se centran en abordar los problemas después de que ocurren en lugar de prevenirlos. Este enfoque reactivo conduce a costosas repeticiones de trabajos y, una vez más, a demoras en los proyectos. El impacto incluye costes crecientes del proyecto (hasta el 12% del valor del proyecto puede atribuirse a las repeticiones de trabajos), menor confianza de las partes interesadas, desperdicio de materiales e impacto ambiental.
El conjunto de soluciones de Minitab incluye herramientas de análisis predictivo y mejora de la calidad que son fundamentales para reducir la repetición de trabajos. Los gráficos de control y el análisis de la causa raíz ayudan a identificar señales de advertencia tempranas de defectos y a garantizar que el proceso se mantenga dentro de límites aceptables. Y con el aprendizaje automático, Minitab puede ayudar a su equipo a implementar un sólido programa de mantenimiento preventivo, que puede ahorrarle miles de euros.
3. Los datos subutilizados limitan el poder de toma de decisiones
Los equipos y las empresas de construcción generan enormes cantidades de datos a partir de cronogramas, presupuestos, inspecciones y sistemas de gestión de proyectos.
Pero ¿se utilizan estos datos?
Gran parte de los datos siguen sin utilizarse (o no se utilizan en absoluto) debido a sistemas aislados, falta de integración o capacidades analíticas insuficientes. Sin información procesable, las empresas pierden oportunidades de mejorar la eficiencia y el rendimiento. Esto conduce a oportunidades perdidas de ahorro de costes, toma de decisiones ineficaz e incapacidad de adaptarse a los cambios del proyecto en tiempo real.
Minitab Connect ofrece una potente plataforma para integrar y analizar datos de todas las operaciones de construcción. Los paneles de control simplifican la generación de informes con información en tiempo real, que permite a los equipos realizar un seguimiento de los indicadores clave de rendimiento (KPI), como el progreso del proyecto, la asignación de recursos y las variaciones de costos. Al aprovechar estos datos, las empresas pueden tomar decisiones informadas, optimizar la utilización de los recursos y ajustar las estrategias de forma dinámica.
Tome el control de las ineficiencias
Abordar estas ineficiencias ocultas puede mejorar significativamente el rendimiento de su proyecto de construcción. Al adoptar un enfoque basado en datos y aprovechar herramientas como las soluciones avanzadas de análisis y mejora continua de Minitab, puede eliminar el desperdicio, mejorar la calidad y mantenerse por delante de la competencia.
- Detalles
- Categoría: Comsol
- Visto: 1645
Introducción/Objetivos
La escasez de agua dulce ha impulsado el desarrollo de tecnologías avanzadas de tratamiento de agua, como la destilación con membrana (MD, por sus siglas en inglés).
En el artículo titulado “Simulation of mass and heat transfer in salt-lake brine desalination by direct contact membrane distillation using 3D CFD” publicado recientement en la revista “Journal of Water Process Engineering” se utiliza COMSOL Multiphysics® para simular el proceso de destilación con membrana de contacto directo aplicado a la concentración de salmueras de lagos salados. El objetivo principal es visualizar y optimizar los mecanismos de transferencia de calor y masa cerca de la capa límite de la membrana.
Modelización/Simulaciones
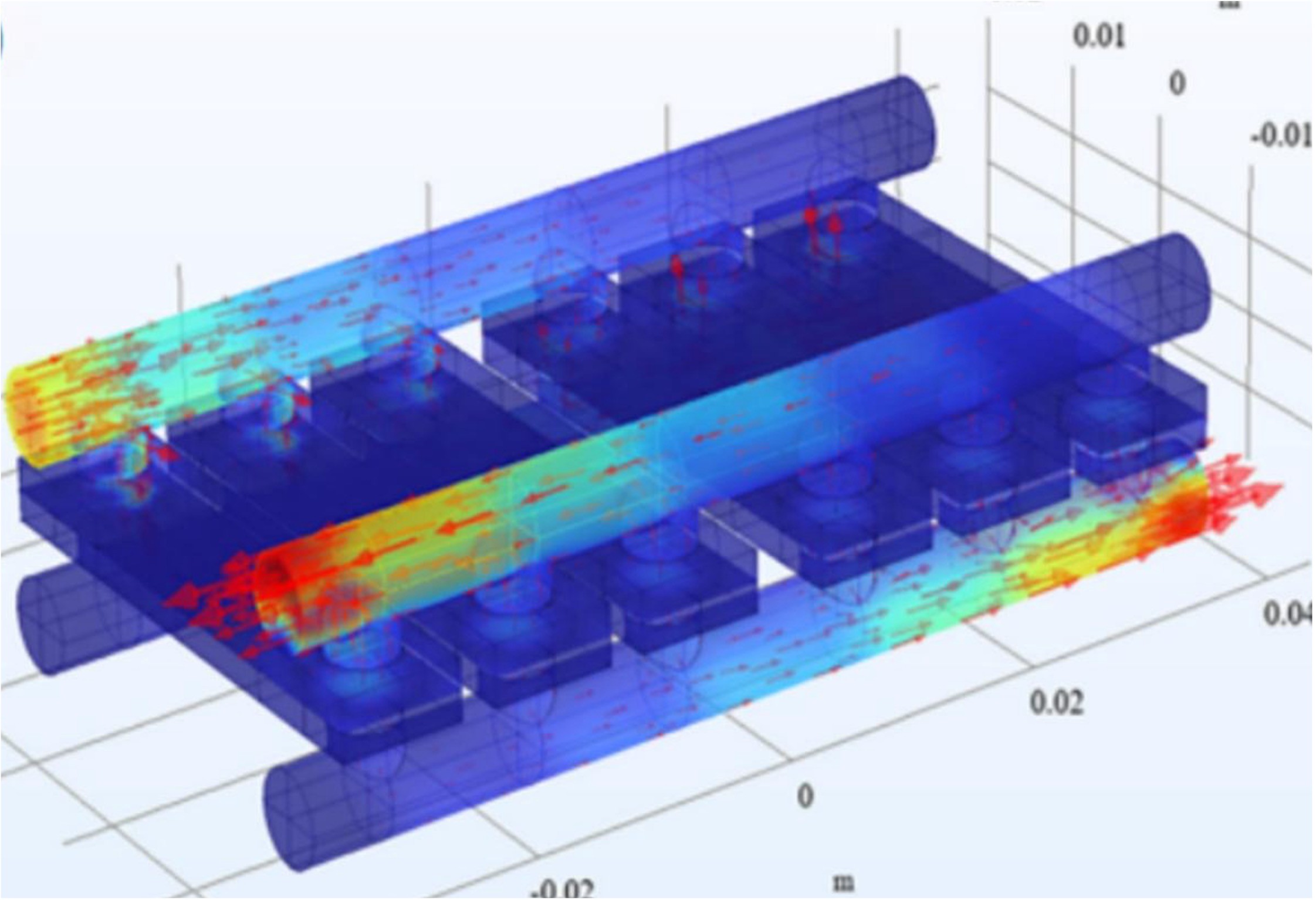
Los autores, Guo y colaboradores, han desarrollado un modelo tridimensional de del módulo de membrana en COMSOL Multiphysics® tal y como se muestra en la Figura 1. El modelo incorpora las ecuaciones de conservación de momento, energía y especies y se construye en base a las siguientes hipótesis principales:
- Equilibrio termodinámico estacionario dentro de la membrana.
- Condiciones de no deslizamiento en las interfaces.
- Propiedades constantes de la membrana y retención completa de solutos no volátiles.
Para garantizar unos resultados precisos en las simulaciones numéricas, los autores utilizaron una malla muy fina. Se evaluaron parámetros como la temperatura de alimentación y la velocidad de flujo, analizando su impacto, por ejemplo, en el flujo de permeación.
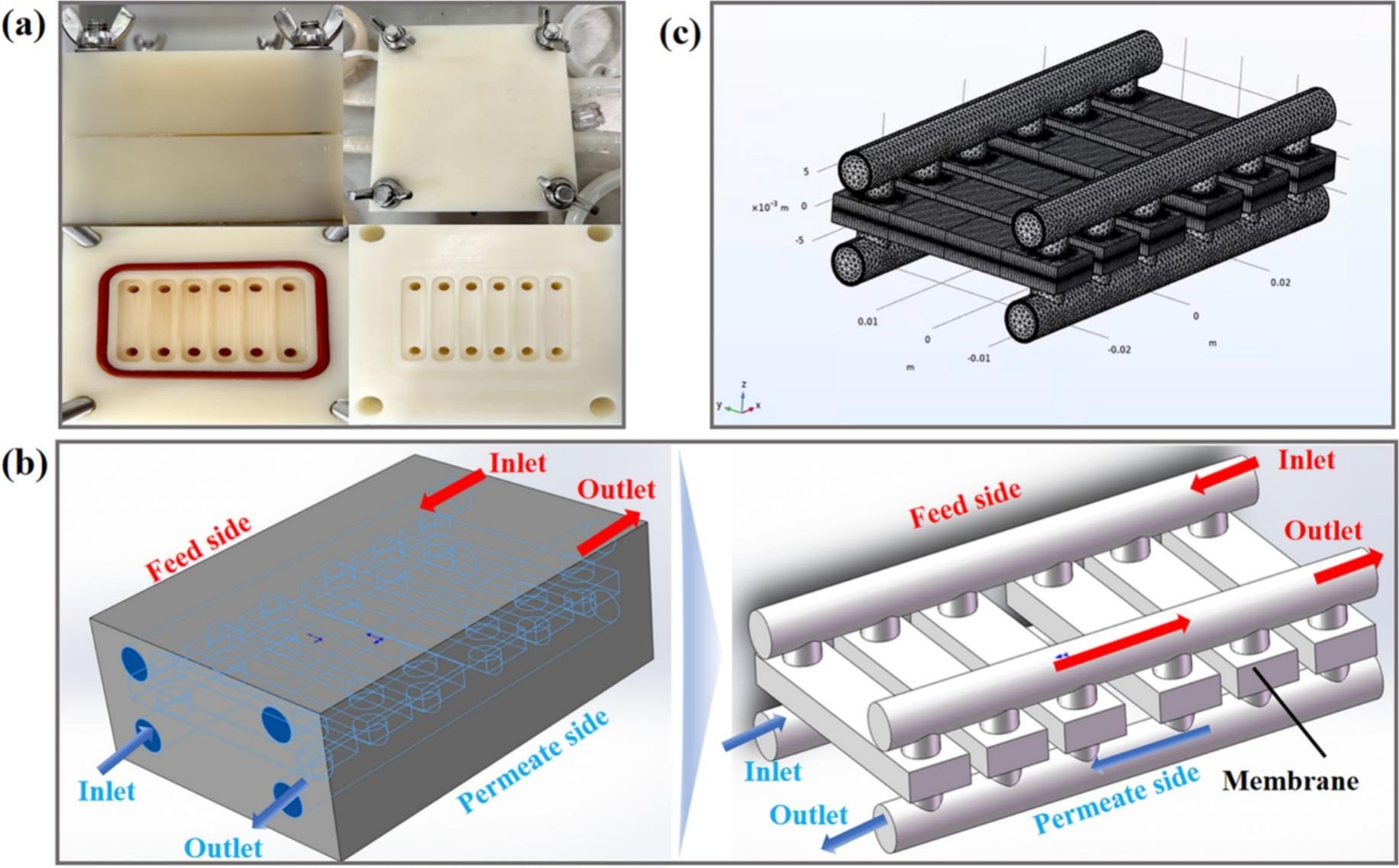
Figura 1. Geometría tridimensional del módulo de membrana DCMD: (a) Estructura del módulo de membrana. (b) Geometría del módulo de membrana. (c) Malla tridimensional para la simulación CFD en COMSOL Multiphysics®.
Resultados/Conclusiones
Los resultados de la simulación mostraron un excelente ajuste con respecto a los datos obtenidos experimentalmente, con un error máximo del 2,49 % en el flujo de permeación. La temperatura de alimentación tuvo un impacto significativo en la transferencia de calor, donde temperaturas más altas mejoraron el flujo. El modelo desarrollado permitió visualizar exitosamente las distribuciones de temperatura (Figura 2) y velocidad (Figura 3), mostrando contornos de temperatura simétricos en ambos lados de la membrana.
El estudio demuestra el gran potencial de COMSOL Multiphysics® para modelizar y optimizar procesos de destilación empleando tecnología de membranas, ofreciendo una herramienta clave para escalar esta tecnología a aplicaciones industriales.
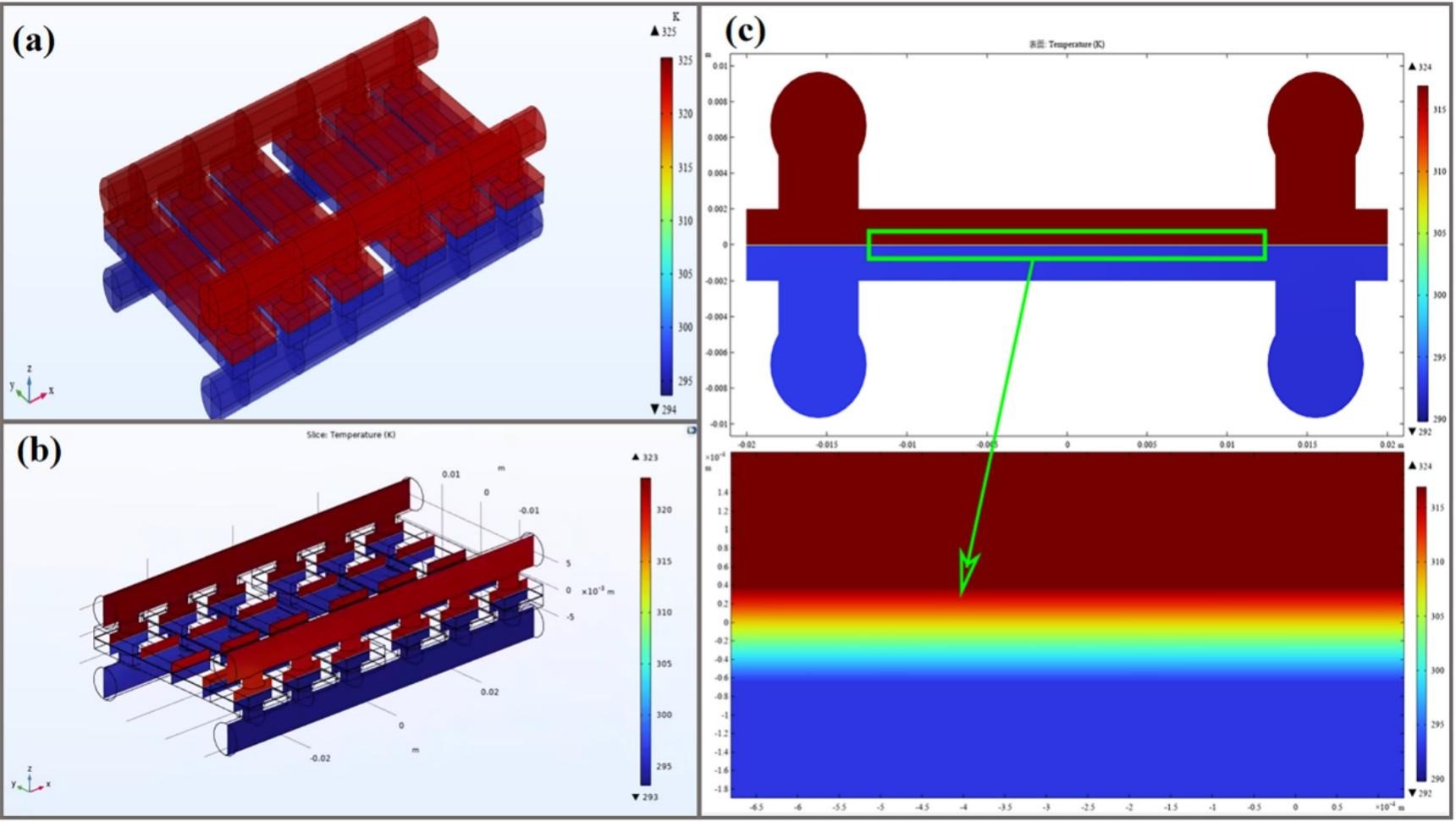
Figura 2. Temperatura obtenida en los distintos dominios del módulo de membrana a partir de las simulaciones en COMSOL Multiphysics®.
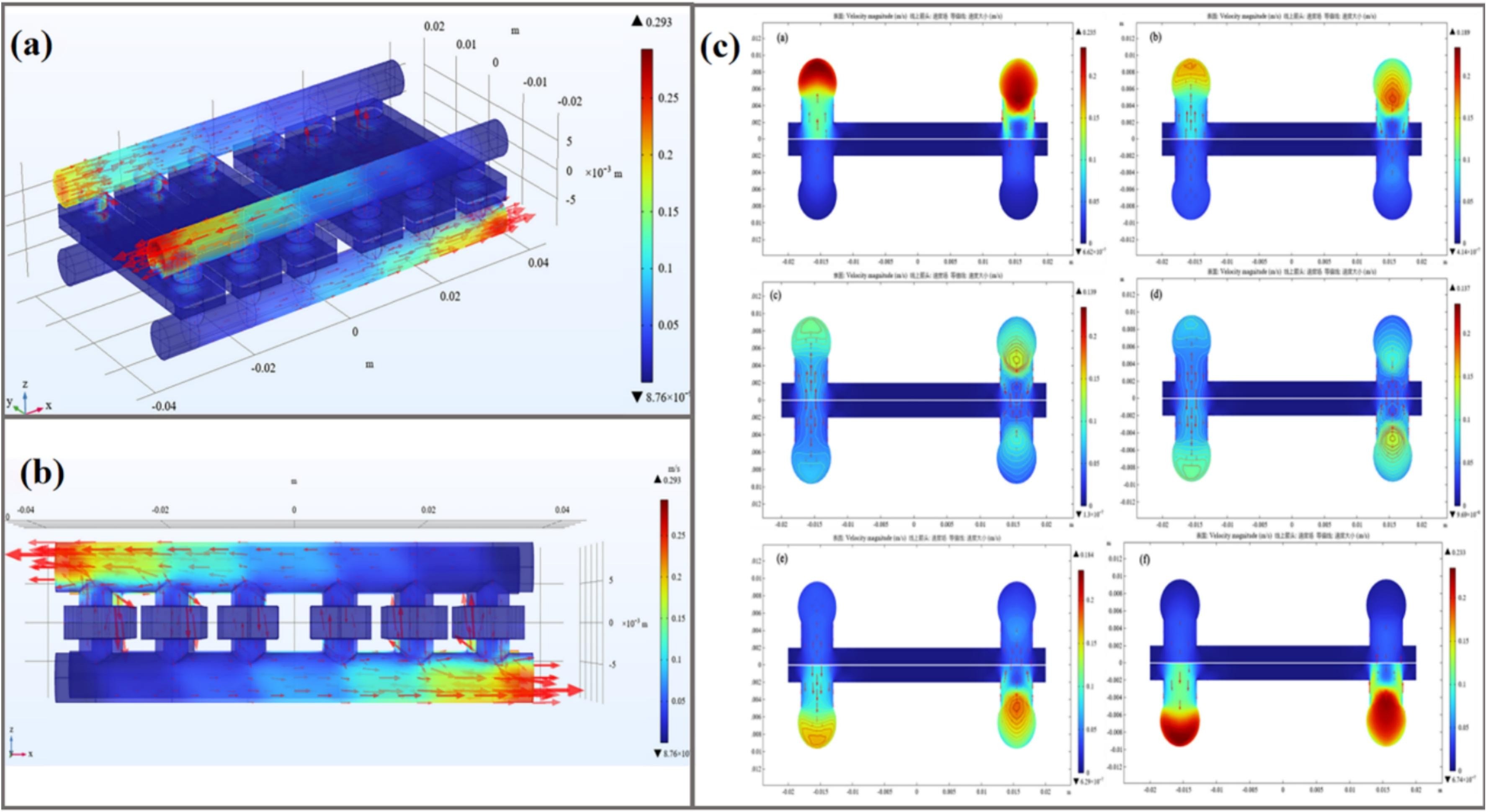
Figura 3. Velocidad calculada para el flujo en los canales del módulo de membrana a partir de las simulaciones en COMSOL Multiphysics®
Referencias
[1] Guo et al. Simulation of mass and heat transfer in salt-lake brine desalination by direct contact membrane distillation using 3D CFD. Journal of Water Process Engineering (2025), 69, 106748.
- Detalles
- Categoría: Systat Software
- Visto: 1622
Introducción
Muchas variables en biología no cumplen con los supuestos de los tests estadísticos paramétricos: no están distribuidas normalmente, las varianzas no son homogéneas, o ambas.
La utilización de un test estadístico paramétrico (como ANOVA o regresión lineal) sobre esos datos puede dar un resultado engañoso.
En algunos casos, la transformación de los datos hará que éstos se ajusten mejor a los supuestos. Existen infinitas transformaciones que se pueden utilizar, pero es mejor utilizar una transformación que se utilice habitualmente en su campo, como la tranformación de la raíz cuadrada para datos de conteo o la tranformación logarítmica para datos de tamaños, antes que una tranformación ambigua de la que no mucha gente haya oído hablar.
También es importante decidir que transformación utilizar antes de realizar el test estadístico.
Las transformaciones matemáticas sobre las variables se realizan a menudo para:
- incrementar la cercanía del ajuste (aumentar R-cuadrado) entre la ecuación de regresión y los puntos de datos,
y/o para - hacer que las variables se ajusten a los supuestos de los procedimientos estadísticos, como la normalidad, y obtener así toda la potencia de esos procedimientos.
Además, las transformaciones de ciertos tipos de variables a veces pueden hacer que las interpretaciones de los resultados de procedimientos estadísticos sean más fáciles y más profundas que sin las transformaciones.
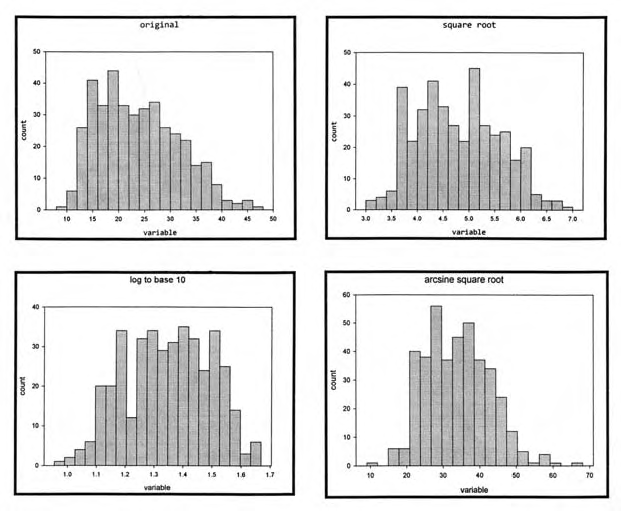
El término "escalera de potencias" (ladder of powers) se refiere a una secuencia de transformaciones algebraicas que pueden realizarse sobre una variable para cambiar la forma de su distribución.
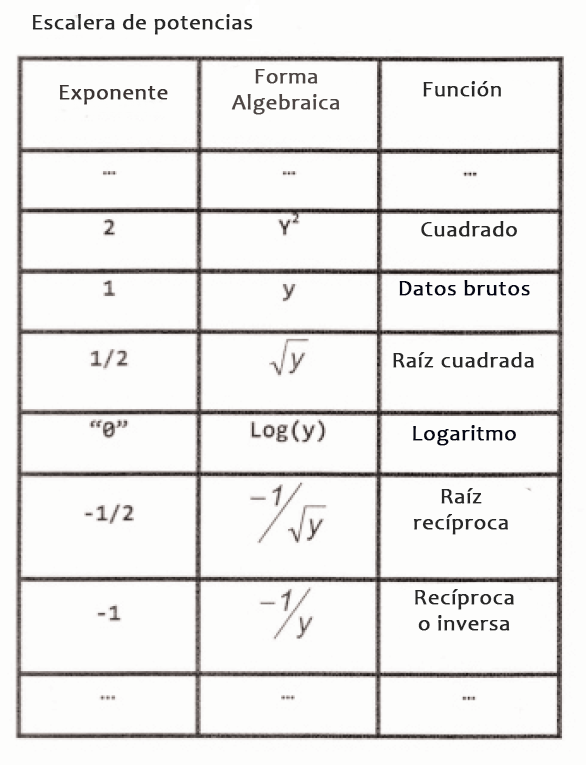
La escalera como se muestra en la tabla superior se enseña aquí para una variable etiquetada "y" que podría ser una variable dependiente o independiente.
Otras potencias y raíces se encajan entre las filas mostradas y se extienden tanto hacia arriba como abajo de la tabla.
Existen muchas transformaciones utilizadas en biología. Las más utilizadas son:
- Transformación raíz cuadrada. Consiste en hacer la raíz cuadrada de cada observación
- Transformación logarítmica. Consiste en tomar el logaritmo decimal de cada observación
- Transformación arcoseno de la raíz cuadrada. Consiste en tomar el arcoseno de la raíz cuadrada de un número.
Transformadas en SigmaPlot
El camino de las transformadas en las nuevas versiones de SigmaPlot se muestra abajo:
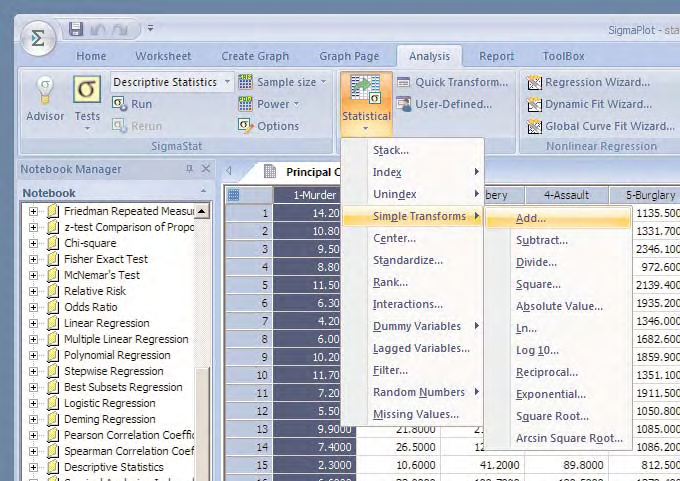
Algunos de los histogramas de las transformaciones de acuerdo con la escalera de potencias utilizando SigmaPlot se muestran en la cabecera del articulo junto con el histograma de los datos originales.
- Detalles
- Categoría: Minitab
- Visto: 1576
El valor de un Análisis de Componentes Principales (ACP) en el análisis multivariante de un técnico de procesos industriales es tan crucial como el de una radiografía para un traumatólogo: imprescindible.
Es un hecho que los repositorios de datos de las empresas están creciendo más rápido que las habilidades para extraer valor de ellos. Además, la implementación de sensórica en los procesos ha permitido una recolección de datos con un nivel de detalle cada vez mayor. Sin embargo, la práctica más común para tratar estos datos sigue siendo una simplificación excesiva, como:
- Resumir mediante el uso de KPIs agregados en medias mensuales para reportes a la Dirección.
- Resumir representando defectos a través de Paretos, gráficos de barras o pasteles.
- Resumir utilizando índices de correlación individuales para describir relaciones entre variables.
El consejo en situaciones donde el proceso o el “paciente” no está estable, y esta inestabilidad es una preocupación, es adentrarse en el detalle de los datos.
En este sentido, el Análisis de Componentes Principales (ACP) se convierte en una herramienta fundamental para comprender los procesos. Por ejemplo, si en una situación se recogen datos de 20 variables cada hora, el ACP reduce la dimensión del espacio a un número mucho menor de componentes, pero que aun así explica la variabilidad del comportamiento entre las horas.
Una visualización de las variables proyectadas en las primeras dos componentes puede ser extremadamente útil para los expertos, ya que les permite identificar de manera clara las causas raíz.
REDUCCIÓN DE LA COMPLEJIDAD DE LAS VARIABLES DE TOLERANCIA
Imaginemos el caso de un fundidor de automoción que se enfrenta a 11 nuevas tolerancias sobre vibraciones de piezas. Esta situación resulta abrumadora, dada la cantidad de variables involucradas.
En este ejemplo real se recogieron datos de estas 11 variables en 180 piezas provenientes de 6 posiciones (o huellas) en el molde. El análisis mediante componentes principales (ACP) aportó valiosas perspectivas:
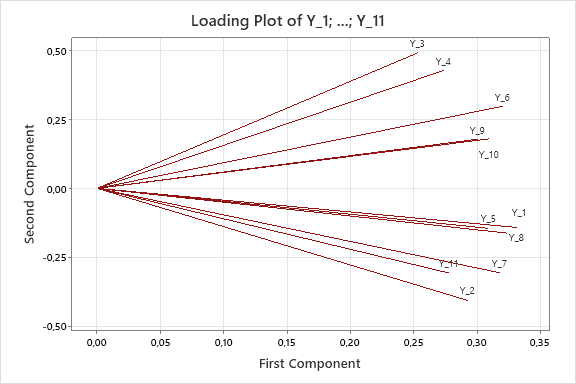
- La alta variabilidad entre las 11 variables se puede reducir a dos componentes principales, lo que implica que el problema es de menor complejidad de lo que parece inicialmente.
- El patrón de variabilidad de las 11 variables tiene una componente común principal (todas aumentan o disminuyen de manera simultánea), lo que sugiere que atacar estos factores clave podría reducir la variabilidad en las 11 características.
- Las variables Y3 e Y4, que son las que más preocupan al departamento de Calidad, están altamente correlacionadas entre sí y presentan componentes de variación de origen diferente.
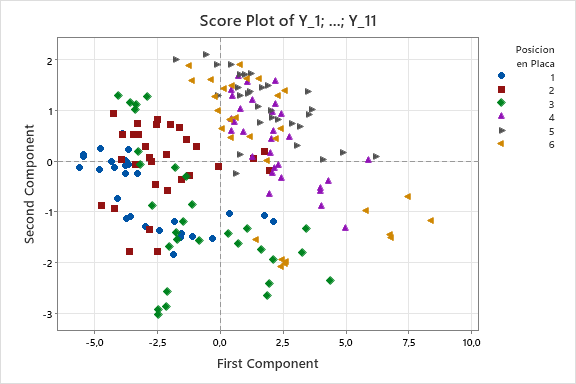
- El gráfico de "scores" muestra cómo cada una de las 180 piezas se distribuye según las componentes que caracterizan las 11 variables, revelando cómo las posiciones de las huellas 1, 2 y 3 se diferencian de las huellas 4, 5 y 6 según las direcciones de Y3 y Y4.
PROFUNDIZACIÓN EN EL ANÁLISIS GEOMÉTRICO
Como resultado de lo anterior, los técnicos decidieron llevar las 180 piezas a metrología para medir 19 características geométricas y así tratar de encontrar patrones que pudieran explicar las variaciones en las variables Y3 e Y4, especialmente las diferencias observadas entre las huellas 4, 5 y 6, en comparación con las huellas 1, 2 y 3.
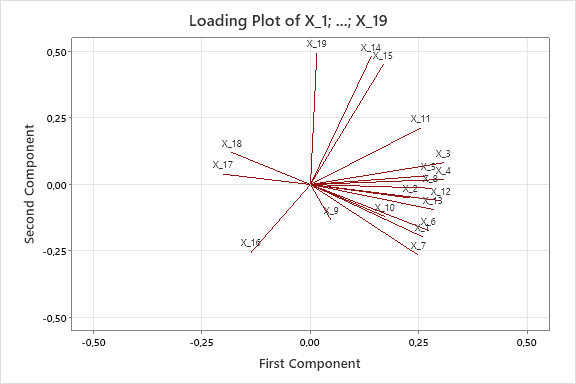
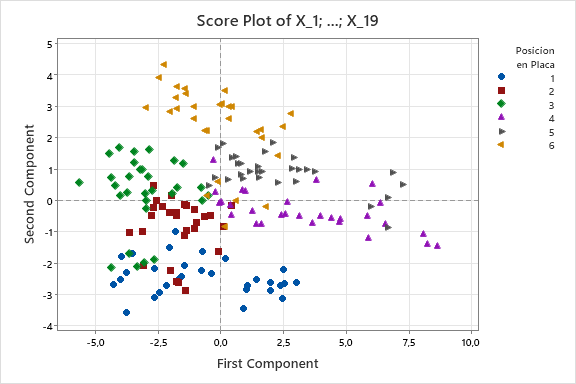
El uso del ACP permitió analizar simultáneamente las 19 características geométricas y arrojó información valiosa, como el hecho de que las huellas 4, 5 y 6, que presentaban valores más altos en Y3 e Y4, tenían dimensiones mayores en las geometrías X5, X4 y X9, mientras que eran menores en X6.
CONCLUSIÓN
Uno de los focos de gran interés en las empresas industriales es identificar las causas raíz de un comportamiento anómalo en los procesos. De manera análoga a lo que ocurre en el ámbito de la salud, cuando hablamos de comportamiento anómalo en los procesos industriales no solo nos referimos al empeoramiento, sino también a las mejoras inexplicables en el comportamiento de estos.
El hecho de contar con un volumen creciente de datos y herramientas como Minitab facilita enormemente el acercamiento al conocimiento profundo del proceso. El Análisis de Componentes Principales (ACP) se presenta como una herramienta clave para abordar problemas multivariantes y permite a los expertos superar creencias erróneas, dirigiendo los esfuerzos hacia la solución adecuada de manera eficiente.
En un futuro en el que las fuentes de datos serán cada vez más diversas y multivariantes, las habilidades para tratar estos datos serán fundamentales.
¿QUIERES APLICAR ESTAS HERRAMIENTAS A TUS DATOS?
Realizar este tipo de estudios no es una tarea difícil si tiene un buen conocimiento de las herramientas de visualización de datos que ofrece Minitab y tiene la habilidad de comprender e interpretar los gráficos.
Precisamente esto es lo que enseñamos en el curso de Diagnóstico con visualización de datos con Minitab.
Si desea recibir una propuesta formal del coste del curso en su caso particular, póngase en contacto con nuestro departamento comercial por teléfono (934154904 o 915158276) o a través de este FORMULARIO
- Detalles
- Categoría: Comsol
- Visto: 1702
Introducción/Objetivos
La optimización del proceso de secado solar es crucial para preservar alimentos como el tomate, con un alto contenido de agua. El artículo titulado “Experimental and numerical study of tomatoes drying kinetics using solar dryer equipped with PVT air collector” [1] empleó COMSOL Multiphysics® para desarrollar una simulación numérica tridimensional (3D) que describe las características de transferencia de calor y masa durante el secado de rodajas de tomate en un secador solar equipado con un colector fotovoltaico-térmico (PVT).
Los objetivos incluyen evaluar el impacto de parámetros clave (temperatura, velocidad del aire y grosor de las rodajas) en la eliminación de humedad y validar los resultados numéricos con datos experimentales.
Modelización/Simulación
El modelo numérico axisimétrico desarrollado en COMSOL Multiphysics® para las rodajas de tomate (Figura 1) acopla las físicas de transferencia de calor en sólidos y transporte de especies diluidas en medios porosos. Para representar la geometría de las rodajas de tomate, se utilizó un cilindro axisimétrico de 35 mm de radio y 22 mm de grosor. Las ecuaciones principales se basan en la segunda ley de Fick para el transporte de agua y en la conducción de calor dentro de la rodaja. Entre las simplificaciones asumidas destacan:
- Propiedades homogéneas e isotrópicas del tomate.
- Transferencia primaria de calor por convección y de masa por difusión.
- Ausencia de contracción del producto.
Se generó una malla de ultra alta resolución con 21,826 elementos triangulares para garantizar la precisión de los cálculos. La simulación evaluó cómo la temperatura, el grosor de las rodajas y la velocidad del aire influyen en la distribución de temperatura y contenido de agua.
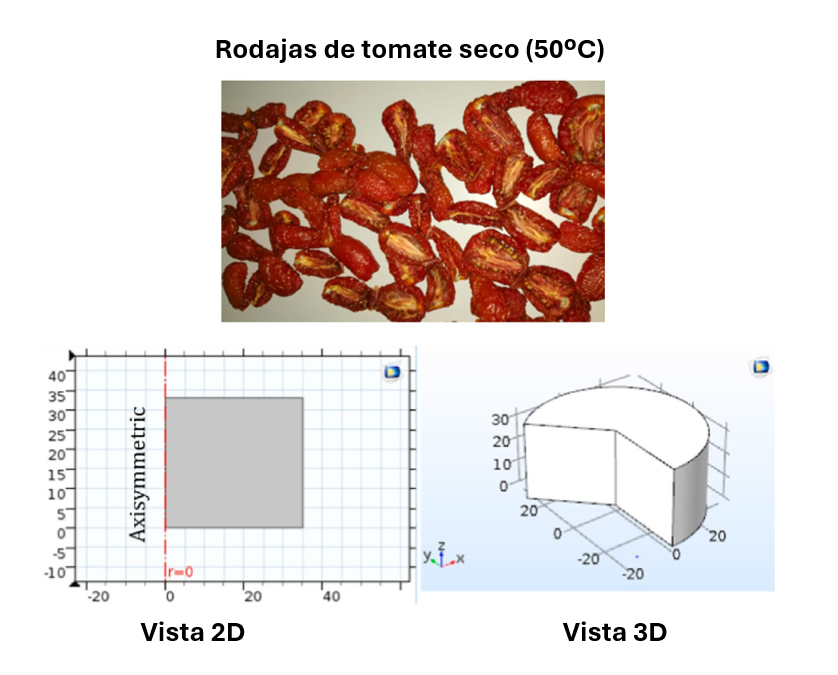
Figura 1. Rodajas de tomate seco modelizadas en COMSOL Multiphysics®.
Resultados/Conclusiones
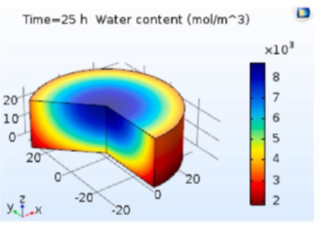
La simulación mostró una alta concordancia con los datos experimentales. De acuerdo con los resultados, a temperaturas de secado superiores a 50 °C la evaporación de agua fue más rápida, evitando contaminación bacteriana. A 60 °C, el tiempo de secado se redujo un 45% en comparación con 40 °C. La Figura 2 y la Figura 3 muestran, respectivamente, el contenido en agua y la temperatura en función del tiempo de secado y la Figura 3 muestra . Los resultados también mostraron que reducir el grosor de las rodajas o aumentar la velocidad del aire permiten reducir el tiempo de secado debido a la menor resistencia al transporte de agua desde el núcleo hasta la superficie. Este estudio destaca el potencial de COMSOL Multiphysics® para modelar y simular procesos de secado de productos agroalimentarios. Su capacidad para predecir la distribución espacial y temporal de temperatura y humedad permite optimizar diseños de secadores y reducir los costos asociados a experimentos físicos. Estos resultados abren la puerta a mejoras en el diseño de secadores solares y sistemas de control automático para procesos industriales.
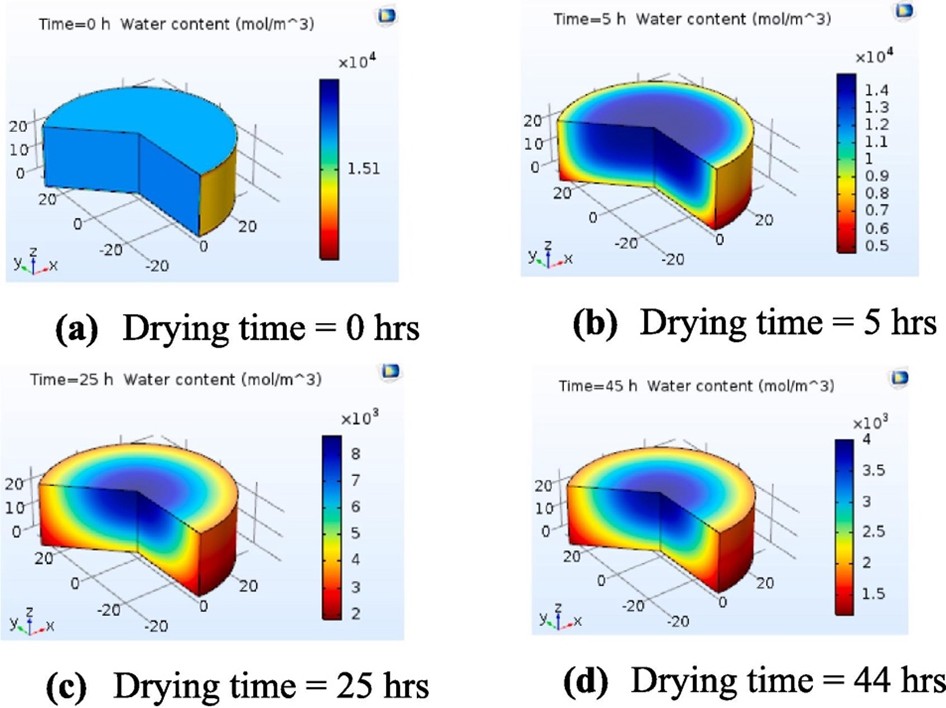
Figura 2. Contenido en agua de las rodajas de tomate calculado en COMSOL Multiphysics® para distintos tiempos de secado.
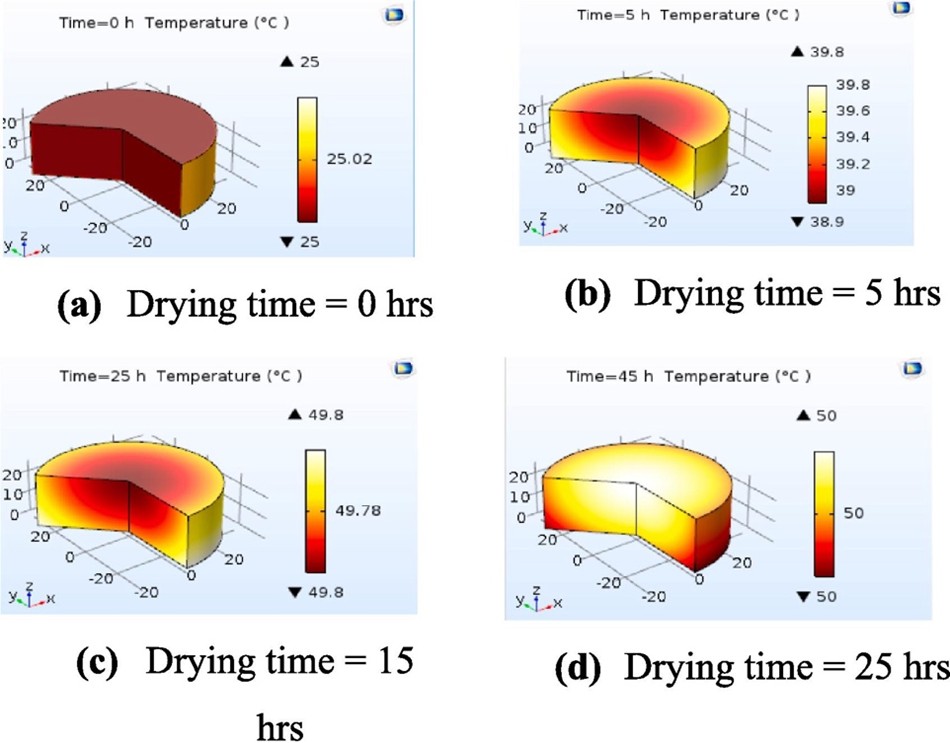
Figura 3. Temperatura de las rodajas de tomate calculado en COMSOL Multiphysics® para distintos tiempos de secado.
Referencias
[1] Fterich et al. Experimental and numerical study of tomatoes drying kinetics using solar dryer equipped with PVT air collector. Engineering Science and Technology, an International Journalt (2023), 47, 101524.