- Detalles
- Categoría: Comsol
- Visto: 5625
Recientemente hemos realizado un Webinar sobre Optimización en COMSOL Multiphysics, utilizando el módulo con el mismo nombre [1]. En esta noticia abordaremos algunos detalles que no se alcanzaron a cubrir. En particular, hablaremos más sobre los Resolvedores del módulo de Optimización.
Antes de entrar en detalle hay que aclarar que en general existen 2 enfoques: Optimización global y Optimización local. Para dar más contexto y poder entender estos conceptos diremos lo siguiente. En un problema de optimización, la función objetivo podría tener múltiples mínimos y máximos (locales). Un algoritmo de optimización global intentará alcanzar, entre todos los mínimos y máximos locales, aquel mínimo o máximo. Por lo tanto, encontrar el mínimo o máximo global es una tarea de mayor complejidad que encontrar un mínimo o máximo local. Así, los métodos analíticos tienen un gran desafío si se quiere trabajar de manera global. Por otro lado, si se especifican buenas condiciones de partida, los métodos locales si pueden ser bastante efectivos, y los métodos analíticos harán su trabajo. Para implementar métodos de optimización global en COMSOL, se puede utilizar el LiveLink for MATLAB.
En el caso del Optimization Module de COMSOL, la mayoría de los métodos de optimización son del tipo local, con excepción del método Montecarlo que si es global. Ahora nos centraremos en las bondades de este módulo, donde la idea es ver las diferencias entre los resolvedores. En la Figura 1, se puede ver una lista de métodos incorporados en el módulo.
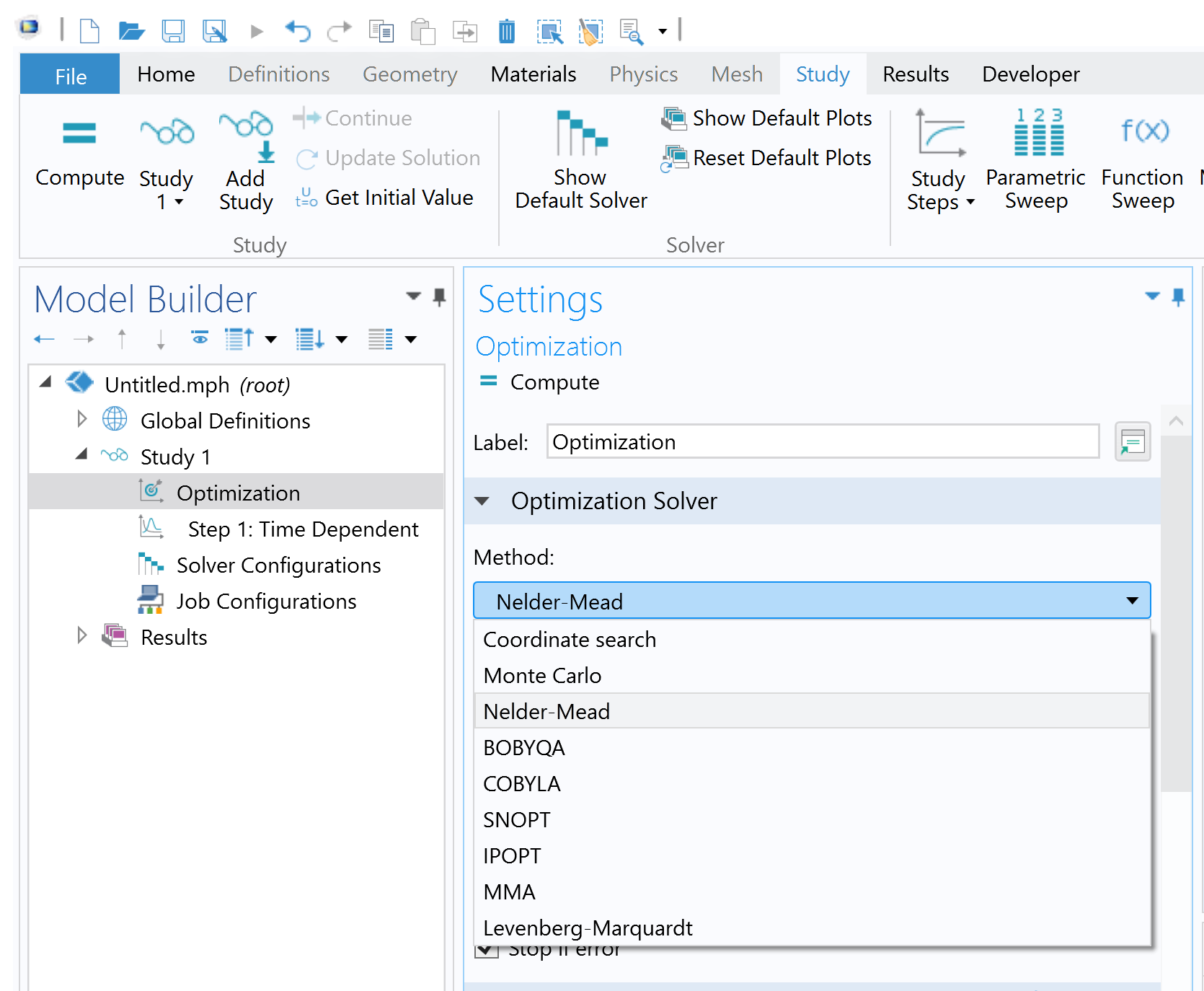
Figura 1: Algoritmos de optimización en COMSOL Multiphysics.
Métodos de optimización en COMSOL
Dependiendo del tipo de problema, hay métodos de optimización más apropiados que otro. Por ejemplo, si alguno de los parámetros de control o diseño implica un cambio en la geometría significa que habrá un remallado. En este caso habrá cambios de geometría inducidos por la modificación de las variables de control. Luego, las variables conducen a diferentes mallas de elementos finitos, superponiendo diferentes errores de discretización en la función objetivo cuando se evalúan para diferentes valores de variable de control.
Teniendo en cuenta lo anterior, podemos distinguir entre métodos de optimización libres del cálculo de derivadas, y que en su defecto realizan una aproximación; y por otro lado, algoritmos de optimización basados en cálculo exacto del gradiente. Una descripción una uno de los métodos libres del cálculo del gradiente y los métodos basando en el cálculo del gradiente viene a continuación.
Métodos libres del gradiente
- Coordinate Search: No evalúa de forma directa el gradiente, sino que va probando algunas direcciones y, de acuerdo con el valor de la función, estima la pendiente de la función en estas direcciones.
- Monte-Carlo: Consiste en probar puntos de manera puramente aleatoria en el espacio de búsqueda.
- Nelder-Mead: Es un método que utiliza simplex que en cada iteración intenta acercarse al mínimo local.
- Bound Optimization BY Quadratic Approximation (BOBYQA): Aproxima la función a minimizar por una función cuadrática. A cada iteración reactualiza su aproximación en función del valor mínimo encontrado al paso anterior. No se basa en el uso de gradiente.
- Constrained optimization by linear approximation (COBYLA): Es similar al algoritmo BOBYQA pero aproxima el problema de optimización con problemas lineales.
Métodos basados en el cálculo exacto del gradiente
- SNOPT (Sparse Nonlinear OPTimizer): Es un método quasi-Newton, el cual debido a que aproxima de forma iterativa las derivadas segundas de la función, puede manejar funciones con muchas dimensiones.
- Mixed Moving Asymptotes (MMA): Es un método de optimización lineal. Se basa en la creación de sub-problemas lineales de optimización donde las cuotas inferiores y superiores (asíntotas) van convergiendo hacia la solución. Usa la información del gradiente para resolver cada subproblema.
- Levenberg-Marquardt: Está basado en una versión del algoritmo de Gauss-Newton. Aproxima de forma iterativa las derivadas segundas lo que le permite trabajar en grandes dimensiones.
Puede verse una comparación de métodos en la Tabla 1.
Comparación de métodos de optimización
En el caso de métodos libre del gradiente, no hay limitaciones extraordinarias. Por otro lado, en el caso de métodos basdos en el gradiente, sí los hay La función objetivo debe ser suave y diferenciable. Asimismo, modificaciones en la geometría tienen como consecuencia que los métodos de optimización libres del gradiente toleren de mejor manera este hecho. Eso porque éstos no confían en la dirección del gradiente para avanzar. La desventaja puede ser el mayor coste computacional y con ello mayor tiempo para resolver.
| Gradiente aproximado | Gradiente exacto | |
| Función objetivo | Cualquier salida escalar | Debe ser suave y diferenciable |
| Variables de diseño | Parámetros globales, incluyendo geométricos | Cualquiera que no resulte en remallado |
| Remallado | Sí | No |
| Restricciones | Solo salidas escalares | Deben ser diferenciables y suaves, pueden estar en cualquier punto del espacio |
| Posibles análisis | Cualquier combinación de los tipos de análisis | Cualquier estudio con sólo un Estacionario, Transitorio o en Frecuencia |
| Desempeño | Aumenta exponencialmente con el número de variables de diseño | No es muy sensible al nº de variables de diseño |
| Tabla 1: Comparación de métodos de optimización según cálculo del gradiente. | ||
App para comparar los resolvedores de optimización
El usuario de COMSOL Multiphysics puede estudiar la convenciencia o no de un método u otro considerando funciones conocidas del ámbito matemático. Dichas funciones están incorporadas como funciones objetivo en una App de COMSOL, descargable de [2]. Pulsando sobre el botón para probar la App, ya se puede utilizar (Ver Figura 2).
Ahora describiremos la App con el fin que el usuario de COMSOL pueda llegar a sus propias conclusiones cuando compare cada uno de los métodos y se aplique a funciones objetivo de distintas características.
En primer lugar, la parte superior izquierda tiene opciones para escoger la función objetivo, todas en el plano XY, y con el valor de la función objetivo pintada de colores cuya leyenda se ve a la derecha del gráfico. Por ejemplo, se tiene: Rosenbrock, Quadratic, Himmelblau, Rastrigin, Beale, Goldstein-Price, Quadratic (discrete), Fish bone, Spiral, Pyramid, etc. Dichas funciones pueden ser lineales, cuadráticas, sueves diferenciables o no, continuas o discretas. Existe una pestaña para añadir restricciones (Constraints). Más abajo se puede especificar los límites inferior y superior para las variables x e y. En la parte media de la pantalla de la App se puede escoger el algoritmo de optimización, así como otras características como la tolerancia y el número de evaluaciones. El resultado se puede visualizar en el gráfico a la derecha. En este caso, se ha usado el algoritmo Nelder-Mead para encontrar el mínimo de la función Rosenbrock. Dicho punto es el (1,1). El botón para iniciar el proceso de optimización se encuentra justo a la derecha donde se escoge el método de optimización.
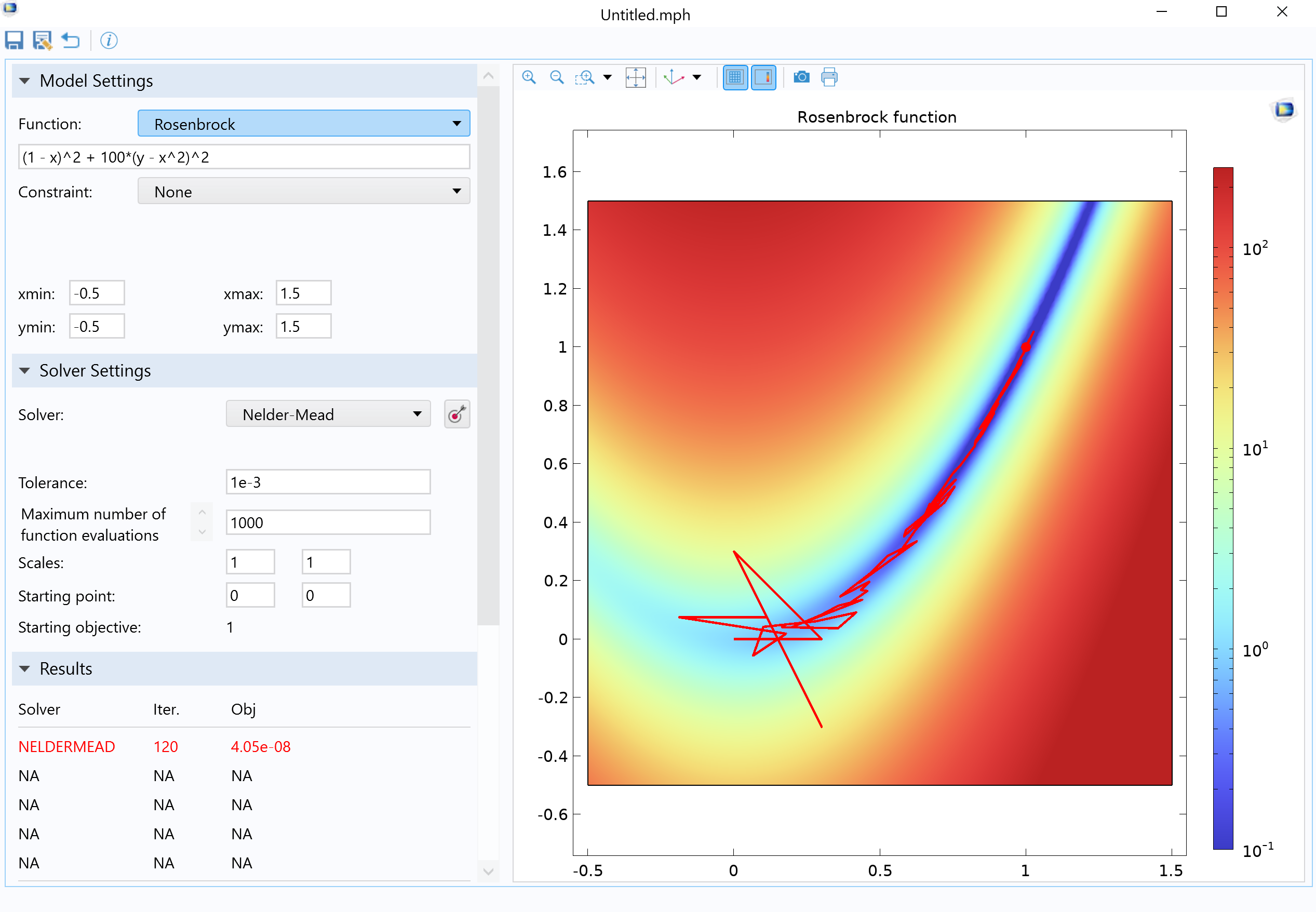
Figura 2: App de COMSOL Multiphysics para comparar métodos de optimización.
Referencias
[1] https://www.addlink.es/eventos/comsol/webinar-taller-introduccion-practica-a-la-optimizacion-con-comsol-multiphysics
[2] https://www.comsol.com/model/optimization-tutorials-71171
- Detalles
- Categoría: Lakes
- Visto: 11864
Las rosas de los vientos se utilizan para representar gráficamente la frecuencia del viento. La comparación directa de rosas de los vientos de dos conjuntos diferentes de datos meteorológicos es una excelente manera de comparar qué tan similares son los datos. Esto se hace comúnmente cuando se comparan datos de observación con los generados con un modelo meteorológico como WRF o MM5.
La aplicación gratuita WRPLOT View de Lakes Software ha sido durante mucho tiempo una herramienta favorita de los científicos en muchos campos diferentes que buscan analizar datos de viento. Cuando se usa WRPLOT View para comparar rosas de los vientos de diferentes conjuntos de datos, es importante comprender lo que se representa para poder realizar una evaluación precisa de los datos.
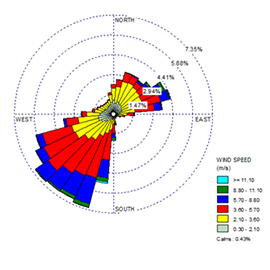
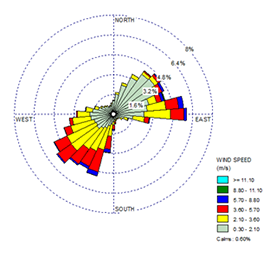
Cuando se carga un archivo de datos meteorológicos en WRPLOT View, la rosa de los vientos que se genera se muestra en una escala que muestra el porcentaje de tiempo que el viento sopla en cada dirección. De forma predeterminada, esta escala se determina automáticamente para ajustarse mejor a los datos.
Cuando se crean dos rosas de los vientos diferentes, es posible que tengan asignadas escalas diferentes de forma predeterminada. En las imágenes a continuación, observe que el primer sitio tiene una frecuencia máxima justo por debajo del 6%, mientras que el segundo sitio tiene una frecuencia máxima cercana al 7,35%.
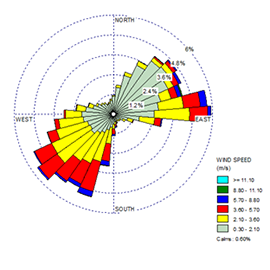 |
 |
Para hacer una comparación precisa, es útil configurar las escalas para que sean idénticas. Para cambiar la escala de una rosa de los vientos en WRPLOT View, haga lo siguiente:
- Haga clic en el botón Options en la pestaña Wind Rose.
- Seleccione Percentage en la opción Scaling.
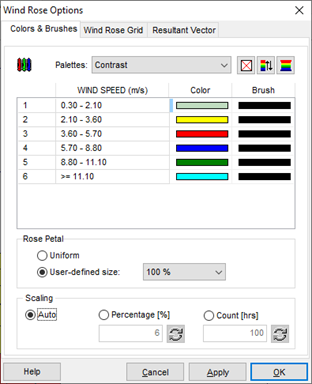
- Especifique la escala deseada
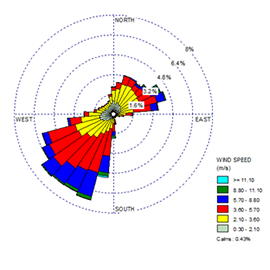
Una vez que las escalas son iguales para ambas rosas de los vientos, es mucho más fácil realizar una comparación visual.
 |
 |
- Detalles
- Categoría: Maple
- Visto: 4908
Por Karishma Punwani
Con el lanzamiento del nuevo Maple 2023, Maplesoft continúa con la misión de proporcionar tecnología potente para explorar, derivar, capturar, resolver y difundir problemas matemáticos y sus aplicaciones, y hacer que las matemáticas sean más fáciles de aprender, comprender y usar. Teniendo esto en cuenta, el equipo de matemáticos y desarrolladores de Maplesoft ha dedicado el último año a añadir nuevas funciones y mejoras que no solo mejoran el motor matemático, sino que lo hacen más accesible dentro de una interfaz fácil de usar.
Y si alguna vez alguien se pregunta de dónde se inspira el equipo de Maplesoft, no necesita ir mucho más lejos de más allá de Maple Primes. Muchas de las mejoras que se han incluido en Maple 2023 han sido el resultado directo de los comentarios de los usuarios. Destacamos algunas de esas funciones solicitadas por los usuarios a continuación, y se puede obtener más información sobre estas y muchas otras mejoras en Novedades de Maple 2023.
- Plot Builder en Maple 2023 ahora permite crear exploraciones de gráficos interactivos donde los parámetros se controlan mediante controles deslizantes o diales, y personalizarlos tan fácilmente como puede hacerse con otros gráficos.
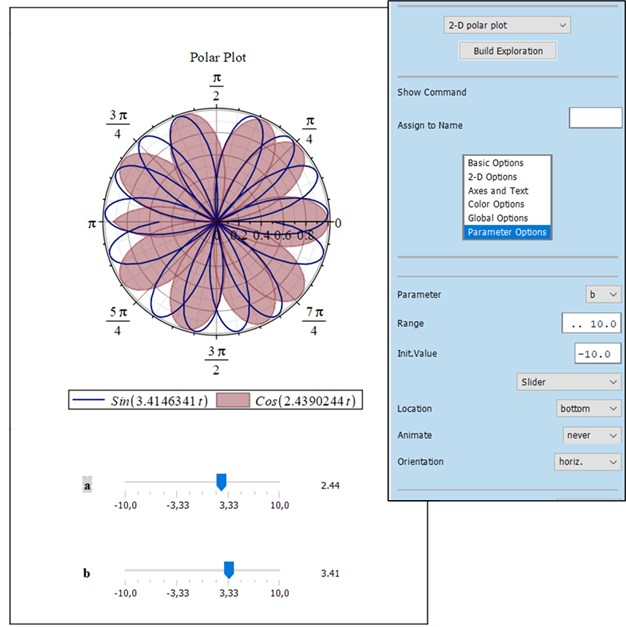
- En Maple 2023, los gráficos de contorno y densidad en 2D ahora cuentan con una barra de color para mostrar los valores de las gradaciones.
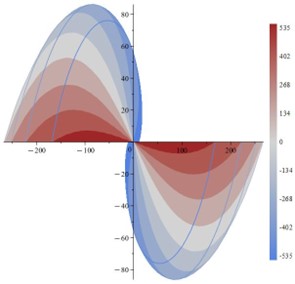
- Para aquellos que escriben mucho código: ahora pueden abrir sus archivos de código Maple .mpl directamente en el editor de código de Maple, donde pueden ver y editar el archivo desde dentro de Maple utilizando el resaltado de sintaxis del editor, la finalización de comandos y la sangría automática.
- La integración se ha mejorado de muchas maneras. Este es uno de ellos: el método de integración definitiva que funciona a través de las circunvoluciones de MeijerG ahora hace un mejor trabajo al verificar las condiciones de los parámetros para que solo se apliquen bajo los supuestos adecuados. También le dice las condiciones bajo las cuales el método podría haber producido una respuesta, por lo que si el problema cumple con esas condiciones, puede añadir las suposiciones adecuadas para obtener su resultado.
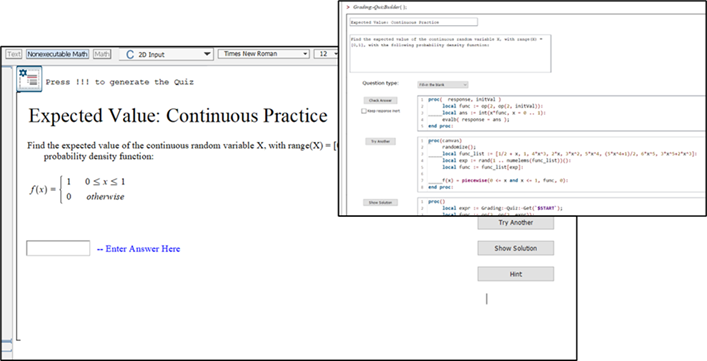
- Muchas personas han pedido que se facilite la creación de aplicaciones matemáticas interactivas más complejas y aplicaciones que requieren programación, como gráficos interactivos en los que se puede hacer clic, cuestionarios que brindan comentarios, ejemplos que brindan pasos de solución. Y me complace anunciar que lo hicimos en Maple 2023 con la introducción de Quiz Builder y Canvas Scripting Gallery.
- El nuevo Creador de cuestionarios viene repleto de cuestionarios de muestra y facilita la creación de sus propias preguntas de cuestionario personalizadas. Inicie el generador de cuestionarios la próxima vez que desee crear cuestionarios interactivos con preguntas aleatorias, diferentes tipos de respuestas, sugerencias, comentarios y mostrar la solución. Probablemente sea una de mis características favoritas en Maple 2023.
- La Galería de secuencias de comandos en Maple 2023 proporciona 44 plantillas y ejemplos modificables que facilitan la creación de aplicaciones matemáticas más complejas y aplicaciones interactivas que requieren programación. El código de Maple utilizado para crear cada aplicación en la galería de secuencias de comandos se puede ver, copiar y modificar fácilmente, por lo que puede personalizar aplicaciones específicas o utilizar el código como punto de partida para su propio trabajo.

- El nuevo Creador de cuestionarios viene repleto de cuestionarios de muestra y facilita la creación de sus propias preguntas de cuestionario personalizadas. Inicie el generador de cuestionarios la próxima vez que desee crear cuestionarios interactivos con preguntas aleatorias, diferentes tipos de respuestas, sugerencias, comentarios y mostrar la solución. Probablemente sea una de mis características favoritas en Maple 2023.
- Finalmente, aquí hay uno que seguramente hará felices a muchas personas: ¡Finalmente puede tener más de una página de ayuda abierta al mismo tiempo!

Para obtener más información sobre todas las nuevas funciones y mejoras de Maple 2023, consulte el documento Novedades de Maple 2023.
Nota: En caso de que no lo sepa, además de Maple, Maplesoft Mathematics Suite incluye una variedad de otros productos de software complementarios, incluidas soluciones en línea y móviles, que lo ayudan a enseñar y aprender matemáticas y cursos relacionados con las matemáticas. ¡Incluso los usuarios ávidos de Maple pueden encontrar algo de interés!
- Detalles
- Categoría: Minitab
- Visto: 4269
Por Stacey McDaniel.
La nube está en todas partes y su alcance se está expandiendo. De hecho, Gartner pronostica que el gasto de los usuarios finales de la nube pública en todo el mundo alcanzará casi 600 mil millones de dólares en 2023. En el mismo informe, Gartner informa que se proyecta que el gasto general en TI crezca un 5,1% este año con la mayoría de las nuevas inversiones destinadas a la tecnología de la nube. Es un momento emocionante y perfecto para adoptar la nube por todos sus beneficios; agilidad y colaboración mejoradas, un impulso útil con grandes innovaciones, tiempo de amortización acelerado y mucho más. ¿Sabe que también puede trasladar sus iniciativas de calidad a la nube?
Si su organización está experimentando una transformación digital, no deje de migrar sus programas de calidad a la nube. Dará como resultado ahorros de tiempo, reducción de desperdicios e ingresos generales. Colóquese en una trayectoria de crecimiento y considere la nube también para la calidad.
Las iniciativas de calidad en la nube se alimentan de la polinización cruzada de información y conocimientos y son accesibles para los empleados en cualquier lugar y en cualquier momento. La capacidad de centralizar datos de calidad facilita la mejora de las operaciones y los informes utilizando recursos de TI mínimos sin necesidad de un centro de datos y sabiendo que las últimas actualizaciones e innovaciones de software se implementarán automáticamente. Minitab tiene herramientas potentes y fáciles de utilizar que le permitirán llevar sus programas de calidad a la nube y garantizar que todos en la organización tengan visibilidad de las iniciativas que se llevan a cabo.
OPORTUNIDADES DE CALIDAD EN TODA LA ORGANIZACIÓN
Minitab ofrece una amplia gama de herramientas de calidad para profesionales. Exploremos las herramientas de mejora de la calidad que están fácilmente disponibles en las soluciones de Minitab que están diseñadas para ayudarle a profundizar y abordar los cuatro factores del marco a continuación:
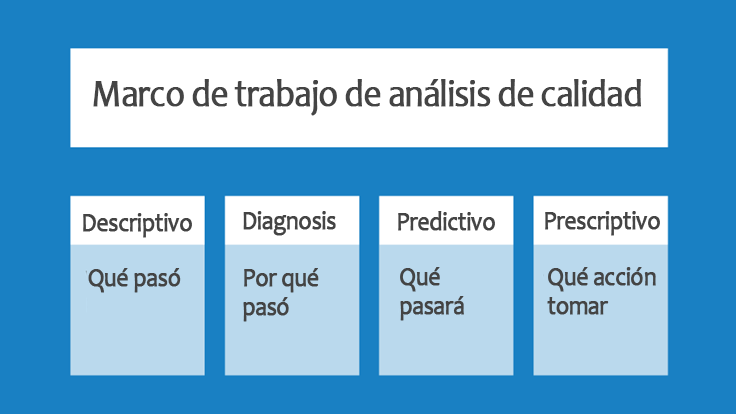
RESOLUCIÓN DE PROBLEMAS CON ENGAGE
Minitab Engage fomenta un programa de calidad colaborativo y está diseñado para ayudar a las organizaciones a crear programas de mejora e innovación en la nube. Las herramientas de resolución de problemas y las metodologías de gestión de proyectos realizarán un seguimiento de las métricas clave de rendimiento en tiempo real para demostrar el ROI. Aquí hay unos ejemplos:
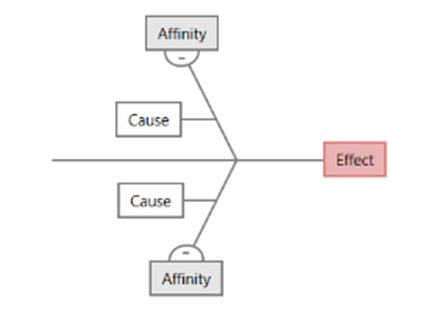
Las espinas de pescado, o diagramas de causa y efecto, ayudan a generar una lluvia de ideas sobre las posibles causas de un problema y a ver las relaciones entre las posibles causas para evitar problemas y garantizar resultados de calidad. En un diagrama de espina de pescado, el problema o efecto central está en el extremo derecho. Las afinidades, que son categorías de causas, se ramifican desde la columna vertebral del efecto central.
Una espina de pesacdo responde a las siguientes preguntas.
- ¿Cuáles son las posibles causas de un tipo particular de defecto?
- ¿Cuáles son las entradas del proceso que contribuyen a la variación en la salida del proceso?
Un mapa de proceso, a veces llamado diagrama de flujo, se puede utilizar para ayudar a modelar el proceso y comprender y comunicar todas las actividades del proceso, las relaciones entre las entradas y salidas del proceso y los puntos de decisión clave. Engage facilita la construcción de diagramas de flujo detallados o de alto nivel, y también hay una funcionalidad para asignar variables a cada forma y luego compartirlas con otras herramientas que esté usando en Engage.
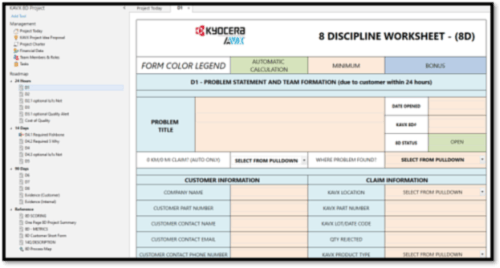
KYOCERA AVX, un cliente de Minitab, trasladó sus plantillas de calidad de Excel a Minitab Engage. Al hacerlo, aumentó la visibilidad de los proyectos de calidad global que se llevan a cabo en sus diversas plantas. Dado que todos en la empresa trabajaban con plantillas estandarizadas, hubo una mejor colaboración e intercambio de información. Engage también ofrece plantillas para 5S, A3, planes de control, los 5 porqués, FMEA y más.
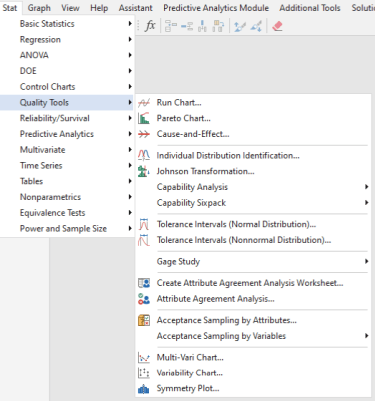
HERRAMIENTAS DE CALIDAD EN MINITAB STATISTICAL SOFTWARE
Eche un vistazo a todas las herramientas y características de calidad incluidas con Minitab Statistical Software. Desde gráficos de control hasta análisis de capacidad, encontrará una herramienta para respaldar su programa de calidad.
Estos son solo algunos de los análisis que pueden contribuir en gran medida a mejorar la calidad.
- Gage R&R puede certificar que la salida tiene el mismo valor que la entrada para garantizar que una empresa esté tomando las decisiones de calidad correctas.
- Los diagramas de Pareto ayudan a descubrir qué falla más y el muestreo de aceptación ayuda a determinar cuántas piezas de producto deben someterse a pruebas de calidad antes de aceptar el producto del proveedor.
- Los gráficos de control también son muy útiles para verificar que los procesos sean estables y, en última instancia, reducir el desperdicio.
- Los análisis de capacidad pueden demostrar la calidad en los procesos que se utilizan.
- Y si alguna vez tiene dudas sobre qué análisis usar, Graph Builder visualiza datos y explora alternativas de gráficos. En función de la entrada, Graph Builder muestra una vista previa de los candidatos de gráficos disponibles.
Al igual que con Engage, Minitab Statistical Software se ejecuta en la nube, por lo que es fácil acceder a él en cualquier momento y en cualquier lugar y compartirlo para facilitar la colaboración. Puede pensarlo de esta manera, usar Engage informa qué datos recopilar y Minitab analiza esos datos para promover la calidad en toda la organización. Son un complemento perfecto entre sí y apoyarán sus iniciativas de calidad. ¡Le invitamos a conocer más!
- Detalles
- Categoría: Minitab
- Visto: 4281
Por Roberto Mastrangelo.
¿Está buscando reducir costes, aumentar la eficiencia de la producción y minimizar el impacto de su industria en el medio ambiente?
Todas las industrias, especialmente las que consumen mucha energía, como la siderurgia, el aluminio, el cemento y la petroquímica, se encuentran bajo una presión constante para enfrentar estos desafíos. Las presiones de la cadena de suministro, la sostenibilidad, los estrictos marcos normativos, las crecientes expectativas de los consumidores y la crisis energética mundial, que ha provocado una explosión en los precios de la energía, han puesto sus márgenes y rentabilidad bajo presión.
Con mucho en juego, las industrias necesitan enfoques sistemáticos y eficientes que puedan identificar rápidamente la configuración óptima del proceso, ahorrar tiempo, costes y recursos.
El método más común para solucionar problemas de calidad y desarrollar mejoras de procesos es el enfoque de un factor a la vez. Sin embargo, este método puede llevar mucho tiempo y ser costoso y, a menudo, produce resultados subóptimos. Además, puede ser difícil obtener información sobre cómo los diferentes factores pueden afectarse entre sí.
¿QUÉ ES DOE?
Existe una herramienta potente y estructurada que puede ayudar a superar estos desafíos: el Diseño de Experimentos (DOE). DOE es un enfoque estadístico que permite a los usuarios investigar la influencia de varias variables en los resultados de interés, lo que lo convierte en una herramienta eficaz para optimizar procesos y productos. Implica realizar una serie de experimentos en los que los factores de entrada se varían sistemáticamente y se miden las respuestas de salida resultantes.
BENEFICIOS DE USAR DOE
Hay muchos beneficios de usar DOE, que incluyen:
- Le permite identificar las variables de proceso más críticas que afectan el consumo y el rendimiento de energía. Al optimizar estas variables, puede reducir el consumo y el desperdicio de energía mientras mejora la eficiencia general del proceso de fabricación. Esto puede ayudarlo a mantener o incluso mejorar la productividad y la calidad mientras reduce su impacto ambiental.
- Otra ventaja de usar DOE es que puede ayudarlo a ahorrar tiempo y recursos en comparación con los métodos tradicionales de prueba y error. Al ejecutar un conjunto de experimentos que varían sistemáticamente los factores de entrada, puede identificar rápidamente la configuración óptima del proceso, ahorrándole tiempo y dinero. Esto se debe a que puede reducir la cantidad de pruebas necesarias, lo que a su vez puede ayudarlo a reducir los costos experimentales.
- DOE permite una comprensión más profunda del proceso de fabricación y sus mecanismos subyacentes. Al proporcionar un enfoque sistemático para explorar el impacto de múltiples variables de proceso en el resultado de interés, puede obtener información que quizás no sea posible con otros métodos. Esto puede conducir a más mejoras e innovaciones, ya que tiene una mejor comprensión de cómo funciona su proceso.
DOE CON MINITAB
Afortunadamente, el poderoso software de Minitab puede ayudarlo con su DOE:
- Minitab proporciona una variedad de técnicas DOE , como diseños de superficie de respuesta, factoriales y de detección para ayudarlo a crear sus experimentos y determinar la cantidad adecuada de ejecuciones y réplicas para que el experimento alcance el nivel de precisión deseado.
- Minitab también puede analizar los resultados de los experimentos e identificar los factores clave del proceso que tienen el mayor impacto en el consumo de energía, el rendimiento y otras respuestas.
- Puede determinar la configuración óptima para los factores clave del proceso utilizando técnicas de optimización como el análisis de deseabilidad y la optimización de respuesta.
- Minitab puede proporcionar alertas y análisis de datos en tiempo real para identificar y corregir cualquier desviación de la configuración óptima del proceso, lo que facilita la ejecución de experimentos de verificación que confirman si la solución óptima proporcionada por el DOE es válida o no.
- Finalmente, Minitab puede ayudar a las empresas a documentar los resultados de los experimentos y compartirlos con otras partes interesadas de manera efectiva.
Minitab Statistical Software puede ayudar a las empresas a reducir el consumo de energía y mejorar el rendimiento al proporcionar un enfoque eficiente para la optimización de procesos a través de DOE. Con sus capacidades analíticas avanzadas y democratización de datos, Minitab permite a las empresas aprovechar al máximo su fuerza laboral y lograr los resultados deseados con un consumo y desperdicio de energía mínimos.
- Detalles
- Categoría: Comsol
- Visto: 5379
El 11 de abril se cumplen 109 años del día en que Albert Einstein (1879-1955) reveló su Teoría de la Relatividad. Sus teorías llevaron a reinventar nuestra comprensión del mundo, convirtiéndose en un icono cultural y figura mundial. Einstein se convirtió en todo esto y más cuando sus teorías de la relatividad especial y general fueron reconocidas como grandes pilares de la física y de la cosmología. El ganador del Premio Nobel revolucionó las ideas aceptadas sobre el tiempo y el espacio para desarrollar sus teorías. Fue uno de los primeros en profundizar en el nuevo campo de la mecánica cuántica, trabajando sobre el efecto fotoeléctrico y la naturaleza de la luz.
La Relatividad y COMSOL Multiphysics
Lente gravitacional
COMSOL permite estudiar fenómenos donde la Teoría de la Relatividad entra en juego. Por ejemplo, el efecto de lente gravitacional [1] se modela usando un índice de refracción que varía continuamente en el espacio, lo cual se conoce como medio graduado. El índice de refracción, n, depende de la constante gravitacional G (unidad SI: m3/(kg·s2), la masa solar m0 (unidad SI: kg), la velocidad de luz c (unidad SI: m/s), y la distancia radial desde el centro del sol r (unidad SI: m), ver Ecuación 1, donde r=√(x2+y2+z2)

La constante gravitatoria es una constante física incorporada con el nombre G_const y con valor predefinido 6.67384×10-11[m3/(kg·s2)]. En este ejemplo, se liberan dos rayos, que rozan la superficie del sol y luego continúan hasta alcanzar una distancia de 150 millones de km. En este punto se evalúa el ángulo de desviación de los rayos desde su dirección inicial. Ver Figura 1.
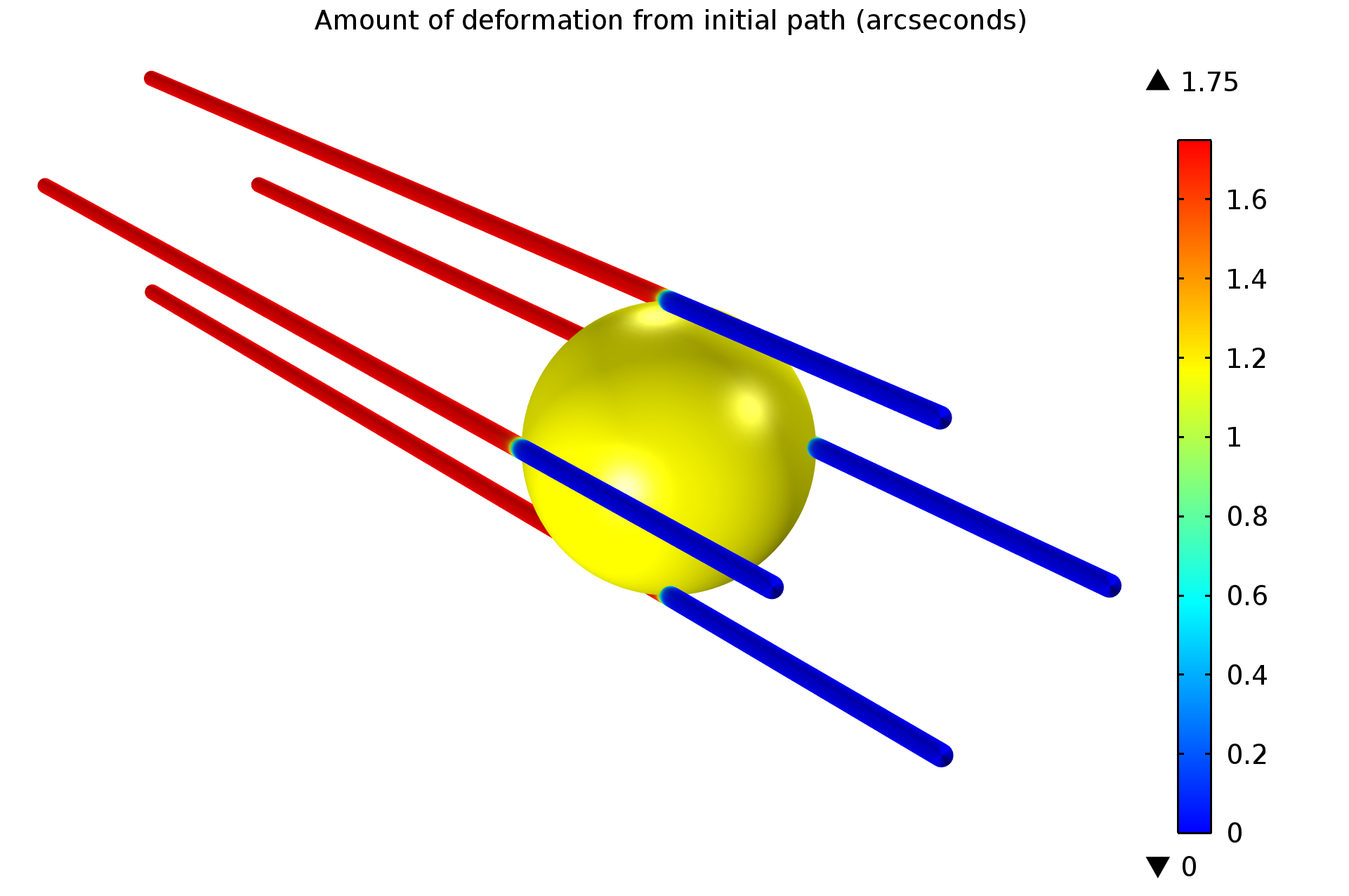
Figura 1: Deformación desde el camino óptico inicial.
El cambio angular en la dirección de los rayos se representa en la Figura 2. Después de la liberación, los rayos necesitan alrededor de 165s para llegar al sol. Los rayos entonces comienzan a desviarse de su dirección inicial debido al gradiente en el índice de refracción. El valor final es de aproximadamente 1,75 segundos de arco, consistente con la predicción de Einstein.
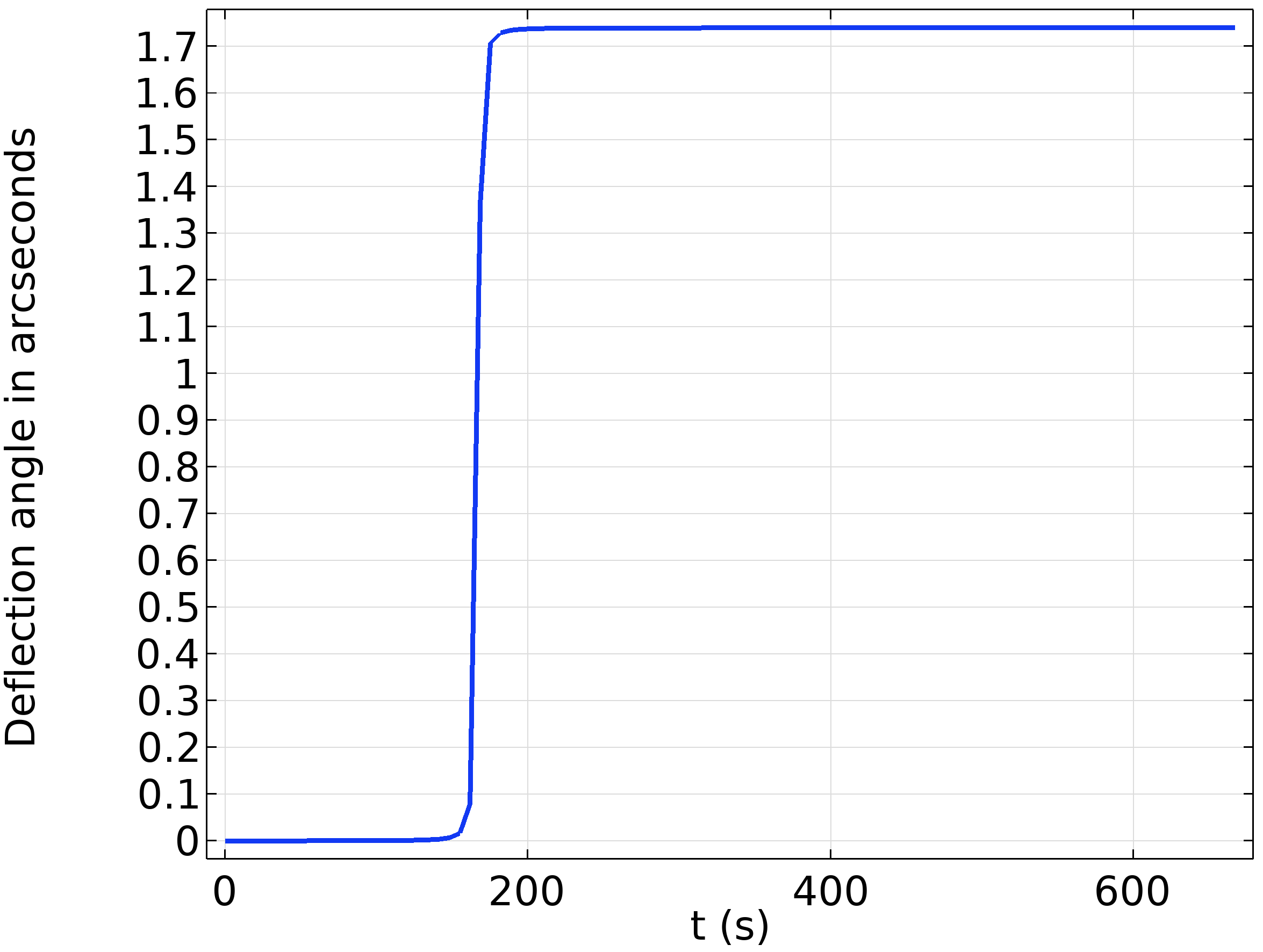
Figura 2: Ángulo de desviación causado por el campo gravitatorio del sol.
Protones en el campo magnético terrestre
Otro gran ejemplo es cuando existen partículas cargadas en las cercanías de la Tierra y son afectadas por el Campo Magnético [2]. En efecto, la Tierra tiene un campo magnético sustancial que se extiende hacia afuera por miles de kilómetros. El campo magnético es generado posiblemente por corrientes circulantes dentro un núcleo líquido de metal girando. Este campo magnético se parece mucho a un campo dipolar; habiendo una inclinación entre el eje de giro de la Tierra y el eje del dipolo magnético.
Para modelar la trayectoria de las partículas, se usa una formulación newtoniana (Ecuación 2), y se aplica una corrección relativista a la masa de los protones estudiados (Ecuación 3). La intensidad de la densidad de flujo magnético y la trayectoria de los protones se ve en la Figura 3 (mr se refiere a masa en reposo del protón).

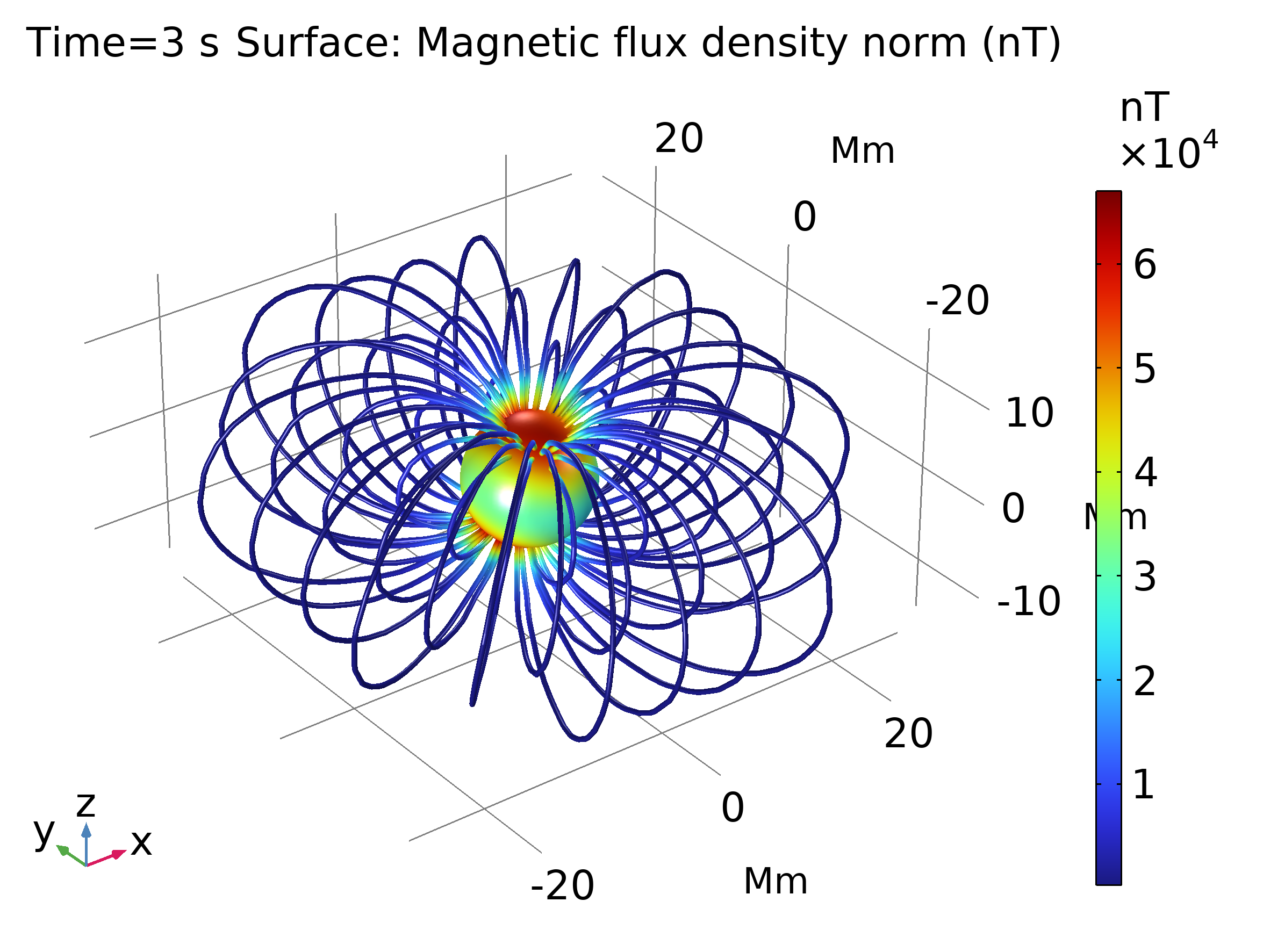 |
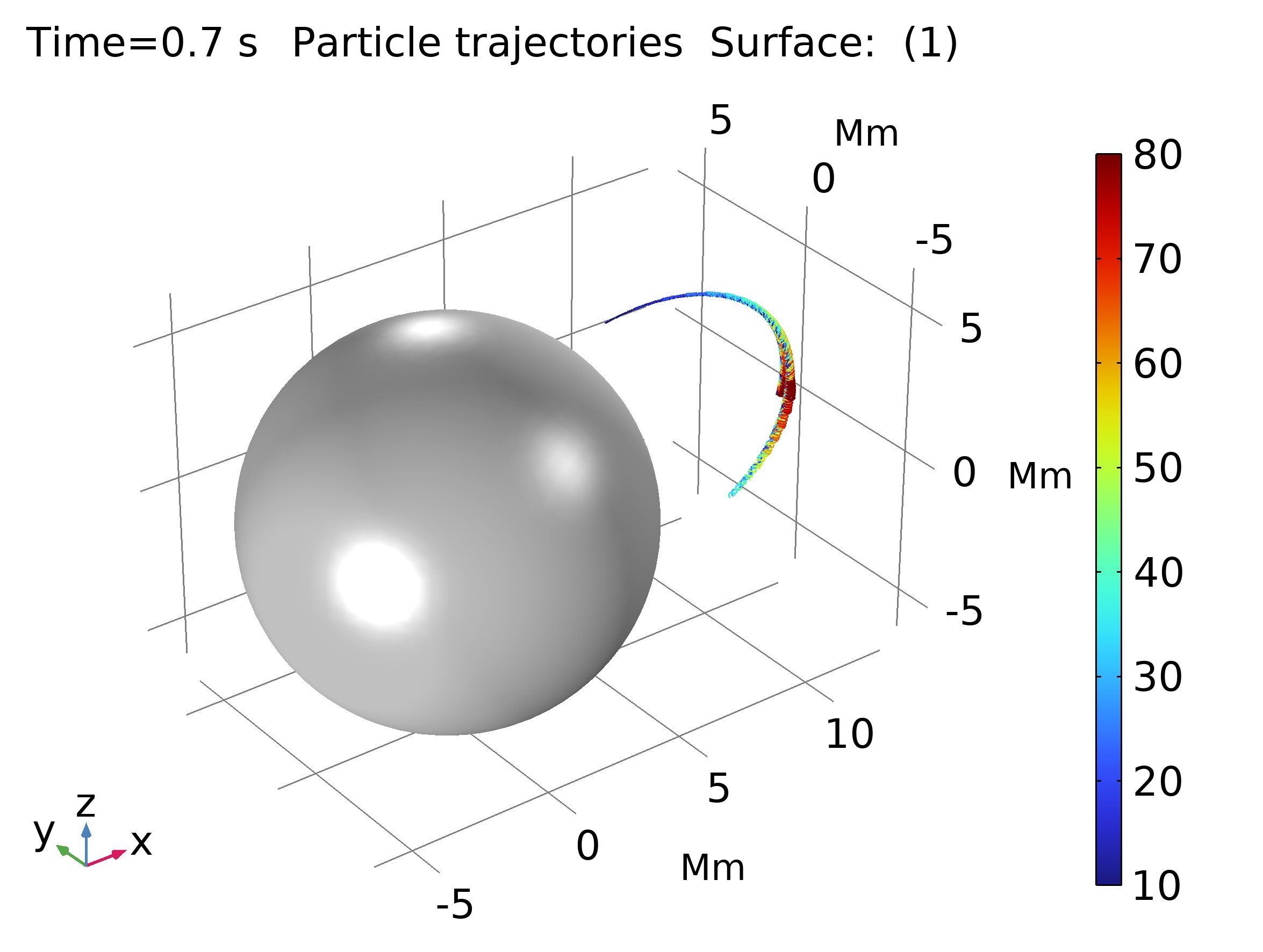 |
| Figura 3. Izquierda: Intensidad de la densidad de flujo magnética. Derecha: Trayectoria de las partículas. | |
Divergencia en un haz de electrones
Un ejemplo similar al anterior permite modelar la propagación de un haz de partículas cargadas a altas corrientes y con velocidades relativistas [3]. Así, la masa de la partícula es corregida mediante la ecuación 3, con la única diferencia que las partículas son ahora electrones. En este escenario, la carga espacial y la corriente del haz crean fuerzas eléctricas y magnéticas significativas que tienden a expandir y enfocar el haz, respectivamente. La interfaz de Charged Particle Tracing puede usar un procedimiento iterativo para calcular de manera eficiente las trayectorias de las partículas fuertemente acopladas y campos eléctricos y magnéticos para un haz operando a corriente constante. En este ejemplo se utilizan otras interfaces acopladas como Electrostatics y Magnetic Fields, ambas acopladas a Charge Particle Tracing. Las trayectorias de los electrones se visualizan en la Figura 4.
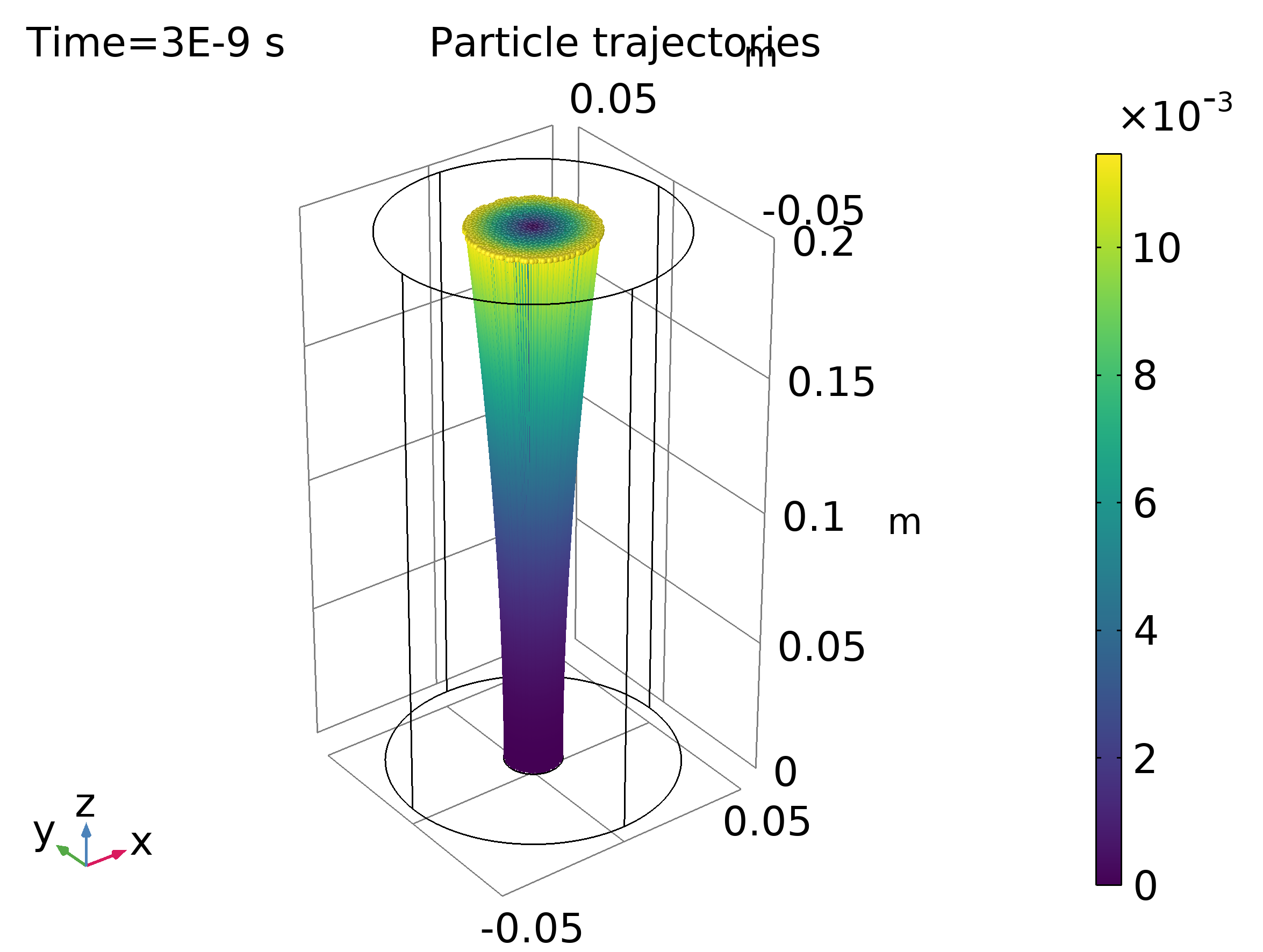
Figura 4: Trayectoria de los electrones.
Otros aportes y ejemplos
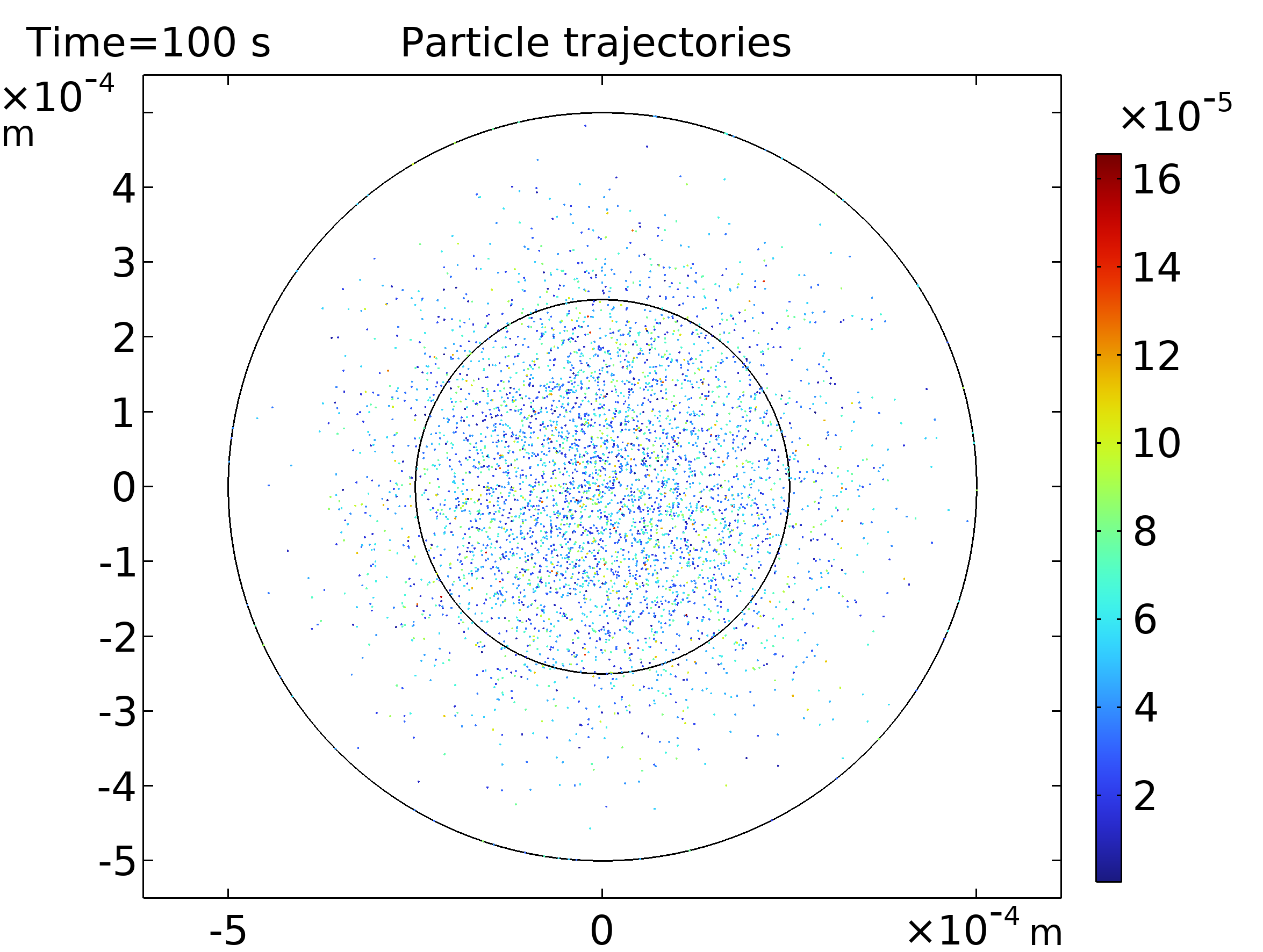
Einstein proporcionó la primera prueba científica de la existencia de los átomos con su teoría cuantitativa del movimiento browniano. Estudió colisiones atómicas en fluidos y demostró que se puede medir el tamaño de los átomos. Este fue un gran avance para el campo de la física atómica. El movimiento browniano sirve para modelar el transporte cuando es de naturaleza puramente difusiva. COMSOL permite hacer la comparación entre los resultados obtenidos utilizando Particle Tracing y Transport of Diluted Species. En la primera interfaz se añade un nodo para incluir la fuerza browniana. En la segunda interfaz se utiliza la ecuación de convección-difusión; sin embargo, deshabilitando la convección [4]. La comparación se puede ver en Figura 5.
 |
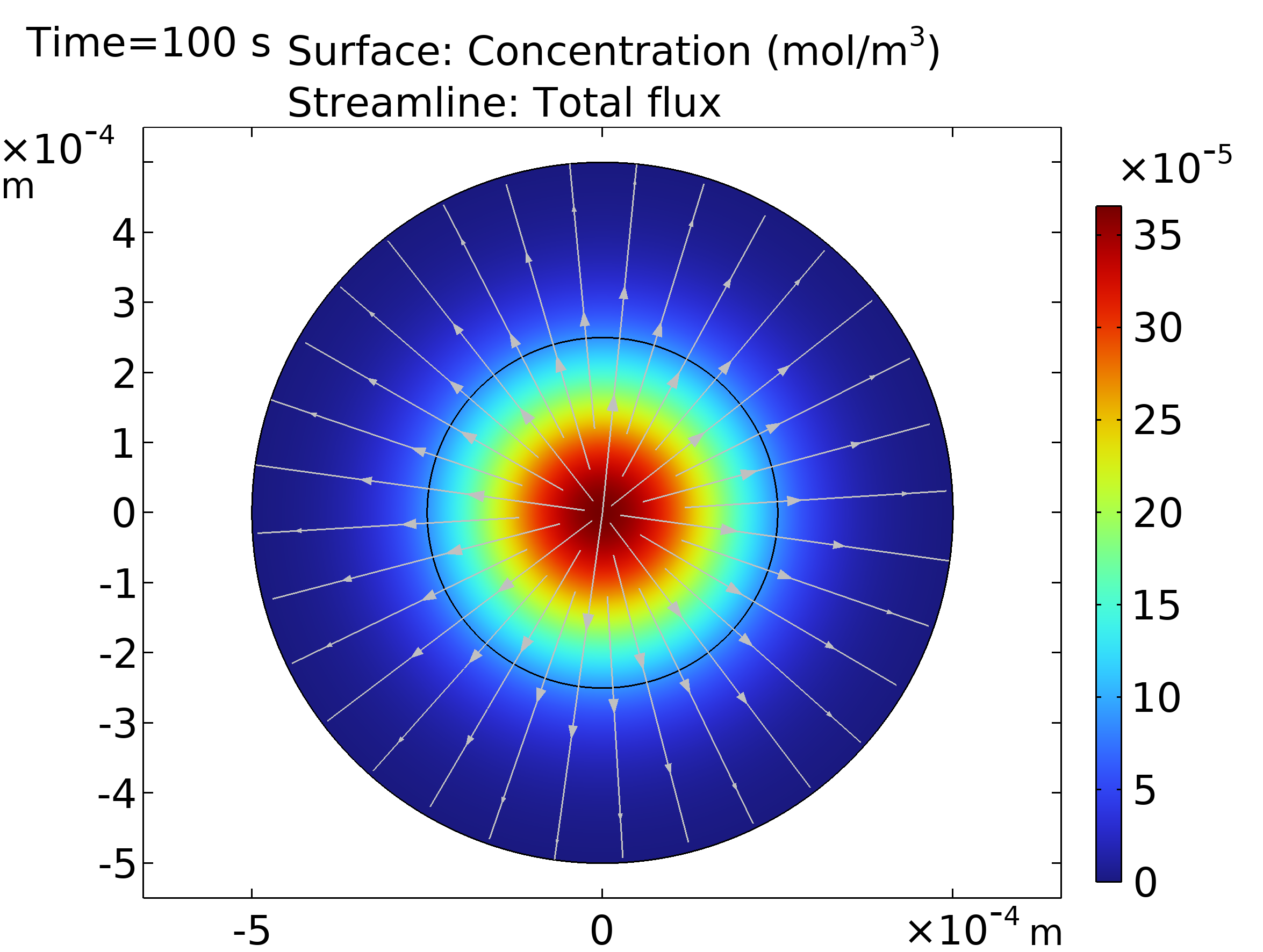 |
| Figura 5. Izquierda: Difusión de las partículas en un fluido usando Particle Tracing y demostrando el movimiento browniano. Derecha: Concentración después de 100 segundos usando of Diluted Species. | |
Referencias
[1] https://www.comsol.com/model/gravitational-lensing-18573
[2] https://www.comsol.com/model/motion-of-trapped-protons-in-earth-s-magnetic-field-19047
[3] https://www.comsol.com/model/relativistic-diverging-electron-beam-17065
[4] https://www.comsol.com/model/brownian-motion-12333
- Detalles
- Categoría: Minitab
- Visto: 4802
Por Oliver Francisco
Cuando se trata de tomar decisiones, es importante tener una comprensión clara de los posibles riesgos y recompensas. Mediante el uso de herramientas como la evaluación de riesgos y el modelado de probabilidad, las personas y las organizaciones pueden tomar decisiones más informadas y minimizar las posibilidades de resultados subóptimos. Esto a menudo conduce a mejores resultados y promueve una sensación de confianza y control en el proceso de toma de decisiones.
Los equipos de investigación y desarrollo suelen tomar decisiones costosas, por lo que es fundamental que mejoren sus procesos para aumentar la probabilidad de obtener resultados positivos. Sin embargo, las organizaciones complejas suelen utilizar sistemas que son demasiado complicados para optimizarlos manualmente, lo que hace que los recursos de optimización sean indispensables para el ancho de banda y el presupuesto.
Ahí es donde entra en juego la simulación Monte Carlo. La simulación Monte Carlo es una herramienta excepcional que puede marcar una gran diferencia cuando se trata de identificar con precisión el mejor resultado posible. Con Monte Carlo, puede probarse sin esfuerzo miles o más configuraciones potenciales, lo que permite tener en cuenta el riesgo en el análisis cuantitativo y procesos de toma de decisiones.
La versatilidad de la simulación de Monte Carlo también se extiende más allá, haciéndola inestimable en el campo de I+D. Afortunadamente, acceder a la simulación de Monte Carlo es simple con Minitab Workspace. Siga leyendo para ver cómo esta potente herramienta puede beneficiar al equipo de I+D.
3 USOS CLAVE PARA I+D
1. Analizar el riesgo
¿No sería fantástico estimar la probabilidad de que se produzcan retrasos en el proceso de desarrollo? O tal vez desee modelar el riesgo de fallo de un producto que desea desarrollar.
Con Monte Carlo Simulation, puede adelantarse a estos inconvenientes y hacer predicciones con mayor confianza. Con el tiempo ahorrado, pueden generarse ideas sobre estrategias para mitigar los riesgos antes de seguir adelante con un desarrollo costoso, y el conocimiento que se obtuvo puede ser muy valioso al trazar el proceso de desarrollo y cronograma.
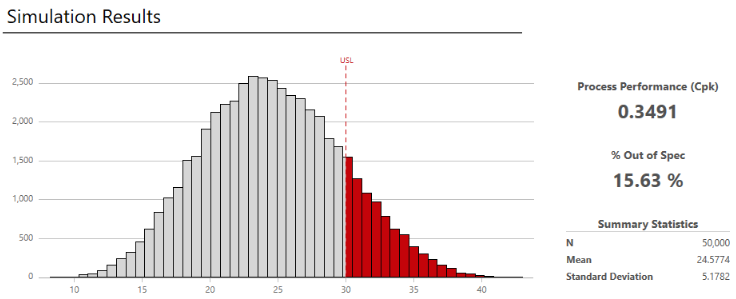
2. Optimizar los procesos
Los equipos de I+D pueden utilizar la simulación Monte Carlo para dar sentido a sistemas y procesos complejos. Específicamente, el equipo puede determinar la configuración óptima para diferentes variables de proceso, como presión, temperatura o caudal. Esto puede ayudar a maximizar el rendimiento y la calidad del producto mientras se ahorra un valioso tiempo y muchos recursos.
3. Mejorar el DOE
Después de realizar el DOE, la incorporación de la simulación de Monte Carlo puede llevar el análisis un paso más allá al permitir simular experimentos y resultados.
Además, al proporcionar una comprensión más precisa de la variabilidad y la incertidumbre, la simulación Monte Carlo puede mejorar la confianza y brindar una mejor comprensión de lo que sucederá cuando se lleve el producto a la planta de fabricación. Esto conduce a un proceso de producción más predecible, lo que puede generar menos errores y productos de mejor calidad.
MINITAB ESTÁ AQUÍ PARA USTED
Se puede acceder convenientemente a Monte Carlo Simulation a través de Minitab Workspace. Esta potente herramienta, junto con muchas otras, puede brindar el poder estadístico para anticipar dónde acabará, antes de comenzar el viaje. Ya sea que desee analizar riesgos, optimizar procesos, mejorar su DOE o las tres cosas, Monte Carlo Simulation puede ayudarlo a lograr sus objetivos.