- Detalles
- Categoría: Minitab
- Visto: 1904
Por David Peralta.
Los equipos de Investigación y Desarrollo manejan diversas tareas relacionadas con el análisis cualitativo y cuantitativo, lo que dificulta mantener toda la información organizada en un solo lugar. Como resultado, esta información a menudo termina dispersa en SharePoint, hojas de cálculo e incluso cuadernos personales. Esta desorganización lleva a que las personas y los equipos dediquen mucho tiempo a reunir estos recursos, lo que prolonga significativamente el ciclo de vida de un proyecto y aumenta los costos.
Pero imaginemos si existiera una herramienta que pudiera servir como centro para almacenar información analítica y cualitativa en una ubicación accesible. Ingrese a Minitab Engage.
MINITAB PARTICIPA EN INVESTIGACIÓN Y DESARROLLO
Minitab Engage es una plataforma integral diseñada para empoderar a los equipos de investigación y desarrollo al optimizar todo el ciclo de vida del proyecto dentro de una sola aplicación, garantizando visibilidad tanto para los miembros del equipo como para las partes interesadas. Esto se hace principalmente en dos áreas clave:
1. Gestión de ideas: un equipo de I+D exitoso prospera gracias a una cultura de creatividad y experimentación. Engage ofrece herramientas para la lluvia de ideas, la generación de ideas y la retroalimentación para inspirar la innovación, todo mientras monitorea y evalúa los objetivos generales del proyecto.
2. Ejecución del proyecto: dado que la incertidumbre y la ambigüedad son uno de los desafíos más comunes que se enfrentan en I+D, mantener la alineación del equipo es crucial. Engage incorpora cuatro características clave que facilitan la ejecución consistente y oportuna del proyecto:
- Hojas de ruta para organizar y guiar proyectos con orientación integrada y mejores prácticas
- Notificaciones y revisiones de fases para que los proyectos no se queden atrás
- Una integración de herramientas clave, como mapas de procesos, diagramas de espina de pescado, planificación DOE, AMEF, mapas de flujo de valor, cartas de proyectos, planes de control, simulaciones CDOV y Monte Carlo.
- Repositorio de datos centralizado para buscar rápidamente trabajos anteriores, compartir mejores prácticas y encontrar oportunidades de replicación
Minitab Engage es una solución sólida diseñada para iniciar, rastrear, administrar y compartir iniciativas de innovación y mejora desde la generación de ideas hasta la ejecución. Engage permite al usuario partir de metodologías de flujo de trabajo estándar y/o definir las suyas propias:
- CDOV
- DFSS (Diseño para Six Sigma)
- DFR (Diseño para la confiabilidad)
- Simulación del Monte Carlo
- Planificación del DOE
- VOC (Voz del Cliente)
- Planificar-Hacer-Verificar-Actuar (PDCA)
- Evento Kaizen
- DMAICO
Además, los datos de los proyectos de Engage se compilan automáticamente en informes de panel interactivos, profesionales y de fácil acceso. Esto mejora la visibilidad de su programa y muestra su éxito:
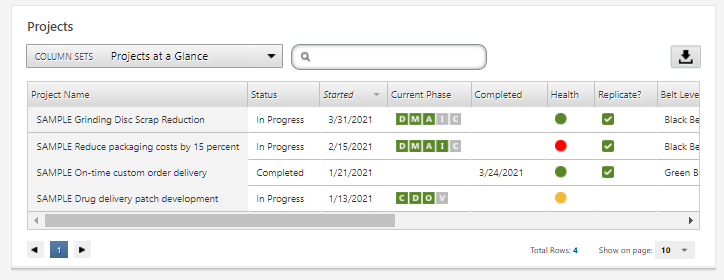
APRENDA MÁS
Minitab Engage es una solución integral para equipos de investigación y desarrollo, que ofrece un centro centralizado para la gestión del ciclo de vida del proyecto. Las funciones personalizadas para la gestión de ideas, la ejecución de proyectos, la simulación y un repositorio de datos sólido garantizan que Engage promueva la eficiencia organizacional al manejar datos e información esenciales cruciales para el éxito del proyecto.
- Detalles
- Categoría: Comsol
- Visto: 2191
Introducción
En COMSOL Multiphysics, la perturbación armónica se revela como una herramienta esencial para analizar respuestas sistemáticas ante excitaciones sinusoidales, siendo crucial para comprender el comportamiento en frecuencia en diversos sistemas, como electromagnetismo, transferencia de calor y mecánica estructural.
Aplicación en electroquímica
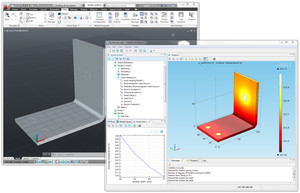
La perturbación armónica en COMSOL Multiphysics destaca en la modelación de experimentos de Espectroscopía de Impedancia Electroquímica (EIS). En este contexto, se convierte en una herramienta útil para estudiar la respuesta de sistemas electroquímicos frente a perturbaciones sinusoidales en voltaje o corriente a diferentes frecuencias. Su incorporación en el modelo permite simular variaciones en la respuesta del sistema, facilitando un análisis detallado de la impedancia en relación con la frecuencia de la perturbación, ofreciendo así una comprensión profunda de las propiedades electroquímicas y la dinámica subyacente. En el ejemplo de modelo y App [1] se puede variar la concentración en masa, coeficiente de difusión, densidad de corriente de intercambio, capacitancia de doble capa, y las frecuencias máxima y mínima para realizar un estudio EIS del sistema electroquímico.
La figura de la cabecera muestra la ventana principal de la App para simular EIS de un sistema electroquímico.
Aplicación en células solares
La Espectroscopía de Impedancia Electroquímica (EIS) se vuelve indispensable en la caracterización de células solares, revelando procesos electroquímicos en diversos componentes. Los autores [2] han desarrollado una aplicación en COMSOL que incorpora la EIS para estudiar células solares, generando gráficos de Nyquist y Bode. Esta herramienta permite la personalización de la geometría y propiedades, esencial para comprender procesos electroquímicos y eléctricos. En resumen, la EIS en células solares ofrece información detallada, fundamental para el desarrollo, optimización y comprensión en términos de eficiencia y estabilidad.
Referencias
[1] Galería de aplicaciones: Electrochemical Impedance Spectroscopy
[2] Joao A. T. P. Vieira & Peter Cendula (2022) SolCelSim: simulación de transporte de carga en células solares desarrollado en Comsol Application Builder, International Journal of Modelling and Simulation, 42:4, 617-627, DOI: https://doi.org/10.1080/02286203.2021.1963144.
- Detalles
- Categoría: Maple
- Visto: 1932
Este vídeo muestra tres maneras en que Maple Flow puede mejorar los cálculos de diseño de ingeniería rutinarios que requieren mucho tiempo para completar.
Esto incluye ofrecer opciones flexibles de diseño y formato, aumentar la confiabilidad de los cálculos (mediante el seguimiento de unidades y realizar funciones matemáticas avanzadas) y promover un flujo de trabajo estandarizado para plantillas de proyectos y hojas de trabajo de diseño.
- Detalles
- Categoría: NAG
- Visto: 8439
En Mark 29.3, NAG presenta un resolvedor de vanguardia (nag_mip_handle_solve_milp) diseñado específicamente para abordar problemas de programación lineal entera mixta (MILP) a gran escala. Esto marca un paso significativo en el compromiso de NAG de mejoar y ampliar sus ofertas en el campo de la optimización matemática.
MILP encuentra una aplicación generalizada en diversas industrias, incluidas, entre otras, la fabricación, la logística, el transporte y las telecomunicaciones. Al acomodar variables de decisión tanto continuas como discretas, el resolvedor permite a las organizaciones modelar problemas prácticos y complejos, incluyendo la asignación de recursos, la programación y el flujo de red.
Problemas MILP a gran escala de la forma
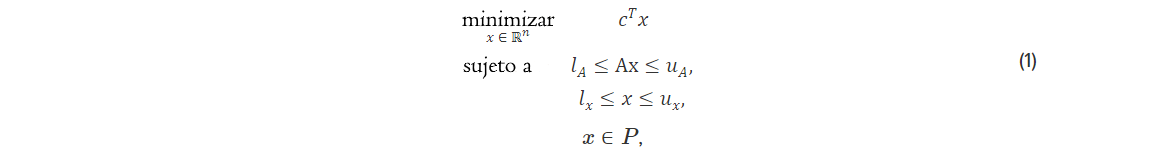
dónde 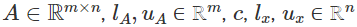 son los datos del problema y
son los datos del problema y 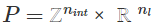 son bastante omnipresentes en aplicaciones de la vida real. Es importante resaltar que resolver problemas MILP plantea un desafío considerable debido a su naturaleza combinatoria y, en muchos escenarios prácticos, encontrar una solución exacta en un tiempo razonable puede resultar muy difícil. Nos complace presentar la última incorporación a la librería NAG y nuestro objetivo es ayudar a los usuarios a tomar decisiones de manera eficiente y precisa.
son bastante omnipresentes en aplicaciones de la vida real. Es importante resaltar que resolver problemas MILP plantea un desafío considerable debido a su naturaleza combinatoria y, en muchos escenarios prácticos, encontrar una solución exacta en un tiempo razonable puede resultar muy difícil. Nos complace presentar la última incorporación a la librería NAG y nuestro objetivo es ayudar a los usuarios a tomar decisiones de manera eficiente y precisa.
Modelado y resolución MILP
El modelo (1) cubre muchos casos de uso práctico. Una de las características distintivas de MILP es su capacidad para modelar condiciones lógicas como implicaciones o dicotomías.
Tomemos como ejemplo el modelado de carga fija. Las actividades económicas frecuentemente implican costes tanto fijos como variables. En estos casos, un coste fijo fix solo ocurre cuando variable y es positiva. Dado un coste variable cvar, el coste total cuando y>0 es cfix+cvary y 0 en caso contrario. Es fácil observar que la función de costes no es lineal. Introduciendo una variable binaria x podemos modelarlo como la expresión lineal
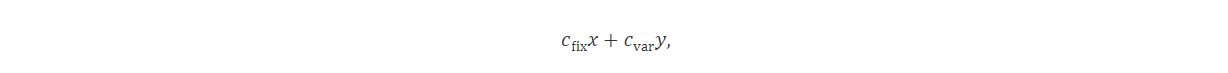
Donde añadimos restricciones
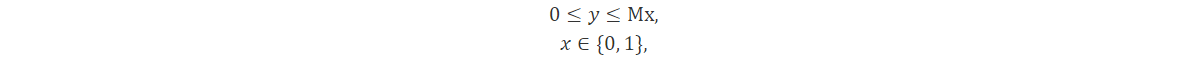
Donde M es un límite superior de y y debe elegirse como el límite más estricto conocido, en lugar de un límite arbitrariamente grande M. Esta técnica de modelado aparece en aplicaciones como la ubicación de instalaciones y el diseño de redes.
Otro gran uso de MILP es modelar disyunciones. Por ejemplo, al programar trabajos en una máquina, es posible que deseemos permitir el trabajo i para ser programado antes del trabjo j o viceversa. Consideremos que pi y pj denotan el tiempo de procesamiento del trabajo i y j, mientras que ti y tj representan sus tiempos de inicio. Entonces requeriremos que se cumpla al menos una de las siguiente restricciones.
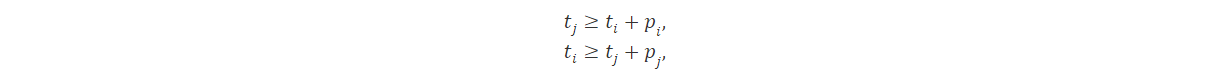
Introduciendo variables binarias x1 y x2 el problema se puede modelar como
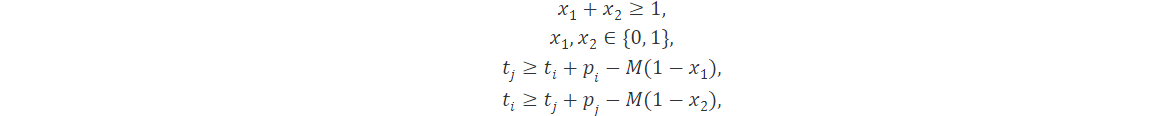
donde M nuevamente es positivo y sirve como límite conocido.
Hay muchos otros tipos de restricciones que son muy útiles en el campo de la investigación de operaciones, incluidas, entre otras,
- Variables semicontinuas donde una variable x es 0 o está en un intervalos [a,b],
- variables que solo toman valores de un conjunto, por ejemplo
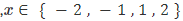 ,
, - funciones lineales continuas por partes, que pueden verse como una combinación de funciones lineales.
Consulte [1,2] para conocer más técnicas de formulación y su uso en la programación.
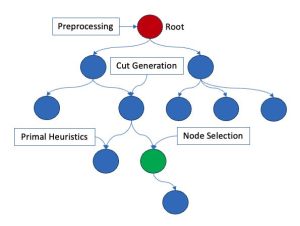
Figura 1: Ilustración de un árbol de ramificación y acotamiento
Para resolver (1) de manera eficiente, el algoritmo de ramificación y acotamiento sirve como marco fundamental, que está equipado con técnicas MILP modernas como preprocesamiento, generación de cortes y diversas heurísticas. En la Figura 1 se muestra una parte de un árbol de ramificación y acotamiento. A partir del problema original, denominado nodo raíz, el algoritmo genera varios nodos secundarios dando forma a la región factible mediante la adición de más restricciones, como el corte fraccional de Gomory. Cada nodo se resuelve como una programación lineal continua mediante un método simplex dual eficiente. Se adoptan varias heurísticas para obtener un mejor límite inferior. Al poder con éxito el árbol de búsqueda y seleccionar los nodos de búsqueda, aumenta en gran medida la posibilidad de que un algoritmo de ramificación y enlace encuentre la solución óptima en un tiempo razonable. Consulte [3] para obtener más detalles sobre algortimos para resolver MILP.
El resolvedor MILP nag_mip_handle_solve_milp está completamente integrado en NAG Optimization Modelling Suite, que permite a los usuarios expresar mejor los problemas del mundo real en el modelo matemático, mejorando la comprensión del funcionamiento interno del modelo. Durante el proceso de modelado, los usuarios pueden
- ver el efecto de una restricción o variable particular eliminándolas temporalmente y luego recuperándolas;
- modificar coeficientes individuales del objetivo lineal o de las restricciones lineales;
- fijar una variable a una constante dada, lo que da como resultado la eliminación de una variable en toda la formulación y la disminución de la dimensión del problema.
El resolvedor está disponible para múltiples lenguajes y entornos, incluyendo C y C++, Python, Java, .NET y Fortran, en Windows, Linux y MacOS.
Referencias
[1] Vielma JP. Mixed integer linear programming formulation techniques. Siam Review. 2015;57(1):3-57.
[2] Floudas CA, Lin X. Mixed integer linear programming in process scheduling: Modeling, algorithms, and applications. Annals of Operations Research. 2005 Oct;139:131-62.
[3] Conforti M, Cornuéjols G, Zambelli G, Conforti M, Cornuéjols G, Zambelli G. Integer programming models. Springer International Publishing; 2014.
- Detalles
- Categoría: Comsol
- Visto: 1959
Introduccion
La simulación acoplada es una característica clave en COMSOL Multiphysics que permite a los ingenieros modelar interacciones complejas entre múltiples fenómenos físicos. En este artículo, exploraremos las aplicaciones prácticas de la simulación acoplada en diversas industrias y cómo COMSOL simplifica la resolución de problemas multidisciplinarios.
Simulación acoplada
La simulación acoplada implica la resolución simultánea de múltiples fenómenos físicos interrelacionados en un sistema o proceso. En el contexto de software de simulación como COMSOL Multiphysics, permite modelar fenómenos como transferencia de calor, mecáncia de fluidos y electromagnetismo de manera conjunta. Esto es esencial cuando los diferentes aspectos físicos de un sistema están estrechamente vinculados y afectan mutuamente, permitiendo así una representación más precisa y completa de situaciones del mundo real.
Aplicaciones
La simulación acoplada en COMSOL Multiphysics ofrece una potente capacidad para modelar la interacción simultánea de diversos fenómenos físicos en sistemas complejos. Desde el diseño mecánico con transferencia de calor hasta la investigación de materiales y la bioingeniería, esta funcionalidad permite abordar de manera integrada desafíos multidisciplinarios. Al acoplar fenómenos como electromagnetismo y estructuras mecánicas, COMSOL posibilita la simulación realista de dispositivos electrónicos, mientra que, en la eficiencia energética, la consideración conjunta de aspectos térmicos, mecánicos y fluidodinámicos lleva a soluciones más eficientes. Este enfoque integral proporciona una visión más completa y precisa de la realidad, impulsando avances de campos ingenieriles y científicos. A continuación mostramos 2 ejemplos representativos. En un primer caso (el busbar) se utilizan interfaces de los módulos de AC/DC, Heat Transfer, CFD y Structural Mechanics. En el segundo caso (dielectroforesis) se utilizan interfaces de los módulos AC/DC, CFD y Particle Tracing for Fluids.
Ejemplo 1: Descripción más integral del modelo
Uno de los ejemplos clásicos aportados por COMSOL es el modelo del "Busbar". En dicho dispositivo se aplica una diferencia de potencial por el que fluye una corriente eléctrica. Debido al Efecto Joule el dispositivo se caliente y disipa energía en forma de calor. Primeramente, el ejemplo de COMSOL modela la convección natural a través del coeficiente de transferencia de calor h. En este caso hemos cambiado la configuración para implementar un "single phase flow" y con ello estudiar en detalle la convección. Finalmente, hemos añadido otro acoplamiento para dar cuenta de la expansión térmica del dispositivo. Así, los nodos de Multifísica son Elecgtromagnetic Heat Source y Thermal Expansion. No obstante, el acoplamiento entre la Transferencia de calor y Fluidodinámica se ha hecho de manera manual. Para visualizar el resultado, véase la Figura 1. Se puede apreciar en las paredes del bloque y del busbar la distribución de temperatura. En los cantos del dispositivo se puede ver el desplazamiento debido a la expansión térmica. Además las líneas de corriente representan la magnitud de la velocidad del aire, cuando éste entra por el contorno de la derecha hacia la izquierda.
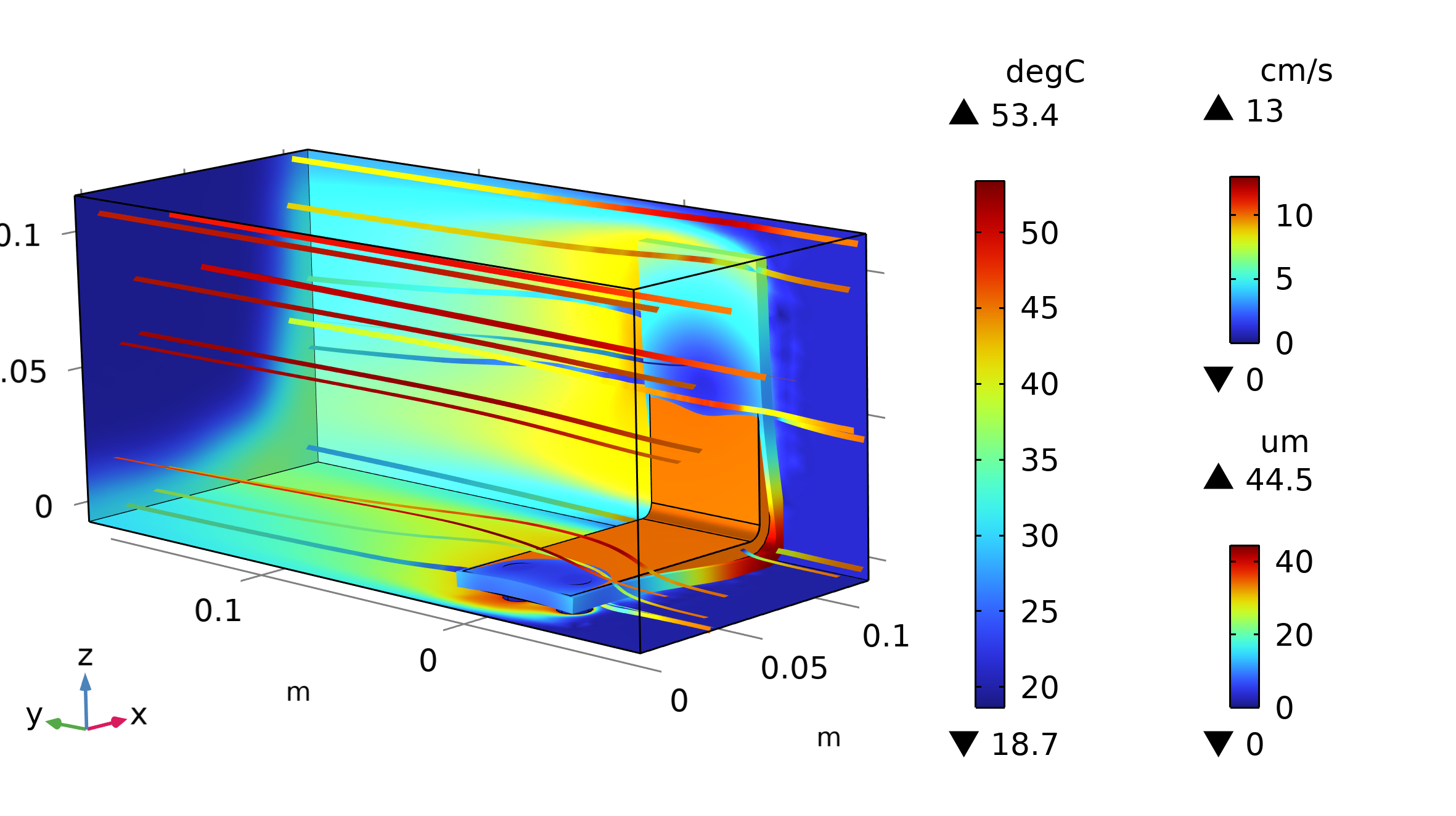
Figura 1: Visualización de la distribución de temperatura (paredes), magnitud de la velocidad del aire (líneas de corriente) y desplazamiento del busbar debido a la expansión térmica.
Ejemplo 2: Dielectroforesis
Otro ejemplo con más de un acoplamiento es el modelo "Dieletrophortic separation" [2]. La dielectroforesis (DEP) se produce cuando una fuerza actúa sobre una partícula dieléctrica sometida a un campo eléctrico no uniforme. Con aplicaciones en dispositivos biomédicos para biosensores, diagnósticos y manipulación de partículas, la DEP se aprovecha de las diferencias en tamaño y propiedades dieléctricas para separar células en mezclas. En el dispositivo DEP de filtrado, las células más grandes, como los glóbulos rojos, se desvían más debido a una fuerza mayor, permitiendo su separación de otras partículas. La aplicación ofrece la posibilidad de ajustar características como el campo eléctrico y propiedades de las células. La descripción de los fluidos requiere el uso de la interfaz de Creeping Flow en CFD. La visualización final de la separación se hace por medio de la interfaz Particle Tracing in Fluids. Ver Resultados en Figura 2.
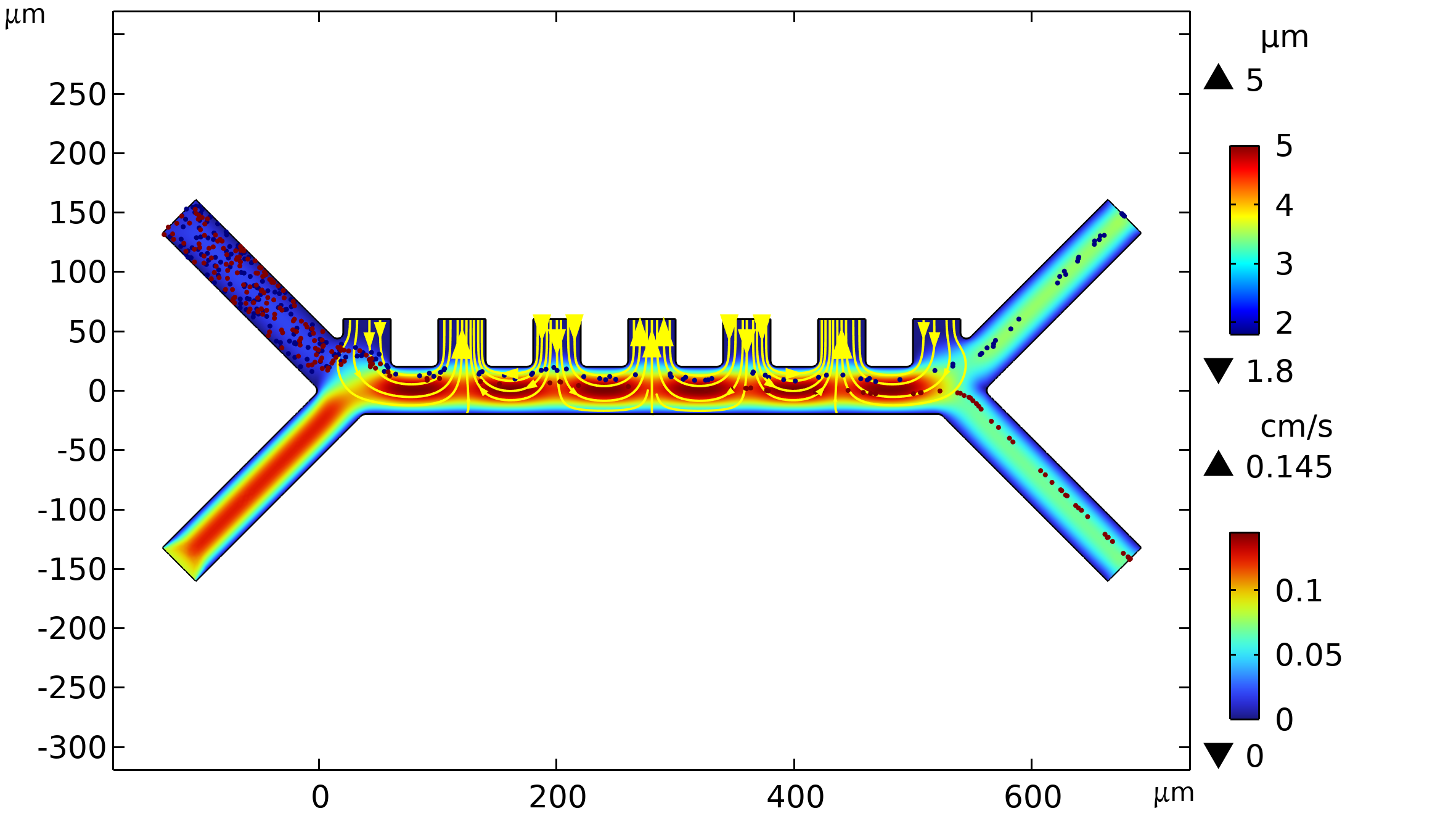
Figura 2: Visualización de la magnitud de la velocidad, partículas (glóbulos rojos y plaquetas en azul) cuya leyenda muestra el diámetro y líneas de campo eléctrico (color amarillo).
Conclusión
La simulación acoplada en COMSOL Multiphysics es un elemento clave, permitiendo la modelación integral de fenómenos físicos interrelacionados. Desde el diseño de dispositivos electrónicos hasta la eficiencia energética y la investigación biomédica, esta capacidad de abordar problemas multifísicos ha llevado a avances en el proceso de diseño y desarrollo. A medida que la tecnología avanza, la simulación acoplada en COMSOL seguirá siendo esencial para enfrentar desafíos multidisciplinarios, transformando la forma en que abordamos problemas complejos.
Referencias
[1] Galería de aplicaciones de COMSOL: Electrical Heating in a Busbar
[2] Galería de aplicaciones de COMSOL: Dielectrophoretic Separation of Platelets from Red Blood Cells
- Detalles
- Categoría: Minitab
- Visto: 2007
Por Óliver Franz.
Un departamento de Tecnologías de la Información (TI) con una importante acumulación de tickets puede indicar varios problemas subyacentes. A los efectos de este artículo, definamos un ticket como un problema planteado por un usuario para notificar a la empresa que su tecnología no funciona como se esperaba.
Independientemente de la causa, el resultado son clientes insatisfechos. De hecho, el problema puede incluso agravarse a medida que los clientes envían varios tickets con la esperanza de una respuesta más rápida, lo que genera un mayor retraso. Al aprovechar Minitab Statistical Software y el Módulo de analítica predictiva, los departamentos de TI pueden identificar la causa raíz del problema y abordarla, lo que resulta en una acumulación de pedidos menor (¡o nula!) y clientes más satisfechos.
UN EJEMPLO DE LA VIDA REAL
Un gran departamento de TI tenía como objetivo reducir el tiempo necesario para cerrar tickets de servicio a medida que crecía el trabajo pendiente. Para lograr esto, el líder del equipo buscó identificar los escenarios (es decir, variables) que tuvieron el impacto más significativo en el cierre de tickets. Comprender las causas detrás de la velocidad del cierre de tickets podría revelar la causa raíz del retraso.
Para abordar el problema, el departamento decidió examinar los tickets que se cerraron más rápido para comprender las razones subyacentes. Al aplicar estos conocimientos, podrían acelerar el cierre de otros tickets. Reunieron datos de los últimos diez meses de resolución de tickets y los introdujeron en Minitab Statistical Software, que incluía información sobre los niveles de dotación de personal (es decir, el tamaño del equipo), la cantidad de tareas completadas, encuestas de satisfacción del cliente posteriores a la resolución del ticket y el tamaño del proyecto (medido en una escala del 1 al 5).
LOS RESULTADOS
Tomaron sus datos y los ejecutaron a través del Módulo de analítica predictiva de Minitab para aclarar qué variables tuvieron el impacto más significativo en los resultados. Como no eran científicos de datos, utilizaron el aprendizaje automático automatizado, que está convenientemente ubicado dentro del módulo. Esta herramienta les ayudó a construir un modelo predictivo en cuestión de segundos y les permitió identificar el modelo más preciso a utilizar, identificando de manera efectiva los factores clave en el cierre de tickets. Sin la necesidad de mirar ecuaciones, la observación inicial del equipo se centró en el gráfico de importancia relativa de las variables, que se muestra aquí:
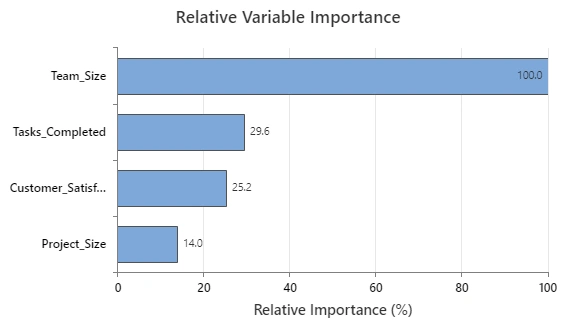
La variable importancia mide la mejora del modelo cuando se realizan divisiones en un predictor. La importancia relativa se define como el % de mejora con respecto al predictor principal.
Estos datos iniciales mostraron que el factor más importante para la velocidad de resolución de tickets es el tamaño del equipo (es decir, el nivel de personal). Curiosamente, las tareas completadas ocuparon un distante segundo lugar, mientras que ni las encuestas de satisfacción del cliente ni el tamaño del proyecto parecieron tener un impacto significativo.
A primera vista, estos datos tenían perfecto sentido para el líder del equipo: cuanto más grande fuera el equipo, más rápido resolvería los problemas.
APROVECHAR EL ANÁLISIS PARA OBTENER CONOCIMIENTOS MÁS PROFUNDOS
Armado con esta información, el equipo ahora tenía motivos suficientes para abogar por personal adicional, pero ¿cuánto? ¡Lo último que querían hacer era contratar a otra persona y no obtener ninguna mejora! Necesitaban entender cómo desplegar sus recursos de manera eficiente y efectiva.
Afortunadamente, la herramienta de aprendizaje automático automatizado de Minitab también equipó al equipo con otro recurso valioso: los gráficos de dependencia parcial de un predictor. Dado que el equipo identificó el tamaño del equipo como el predictor más influyente, podrían dedicar más tiempo a analizar un gráfico de ese factor. Minitab produjo los siguientes resultados:
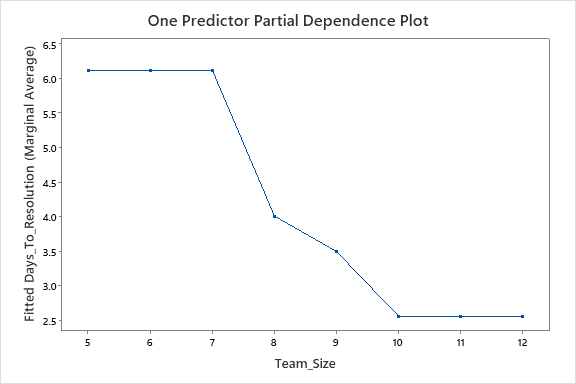
Vemos los resultados promedio de tareas anteriores según el tamaño del equipo. Los datos nos muestran que hay una diferencia significativa en el tiempo que le tomó al equipo resolver problemas en un equipo de siete (aproximadamente 6 días) versus un equipo de diez (aproximadamente 2,5 días), más del doble, de hecho.
Pero los datos también nos muestran que no hay una diferencia aparente entre el tiempo que llevó resolver los tickets en un equipo de diez versus uno de doce. Entonces, en este caso, tiene más sentido dedicar un equipo de diez profesionales de TI a realizar tickets y resolver problemas para lograr la máxima eficiencia. Igualmente importante es que demuestra que, a menos que se haga una inversión sustancial en los niveles de personal, hay poca diferencia entre cinco y siete profesionales, por lo que contratar a un miembro adicional del equipo producirá un impacto mínimo.
Descárguese el artículo "Common Problems Solved by Predictive Analytics", para obtener más información.
PARA LLEVAR
Este resultado es crucial porque, fundamentalmente, ofrece una hoja de ruta para la mejora y una explicación del problema actual. Existe una solución clara para reducir la acumulación de tickets y mejorar rápidamente la satisfacción del cliente.
Además, las visualizaciones generadas cuentan una historia convincente para los tomadores de decisiones de la alta dirección, no solo enfatizando la necesidad de invertir en personal, sino también cuánto personal se necesita para rectificar el problema.
- Detalles
- Categoría: Comsol
- Visto: 2048
El grafeno, el material bidimensional de carbono, se encuentra a la vanguardia de la nanotecnología, ofreciendo propiedades que despiertan la innovación en diversas industrias. En el ámbito de la plasmónica, donde la manipulación de la luz a escala nanométrica tiene un inmenso potencial, las características del grafeno toman el protagonismo.
Un reciente estudio innovador, " Hybrid Approach for Graphene Modeling in Numerical Simulations of Graphene-Based Plasmonic Devices with COMSOL" [1], profundiza en metodologías para modelar dispositivos plasmónicos basados en grafeno utilizando las capacidades de COMSOL Multiphysics.
Esta investigación lidera una estrategia de modelado híbrido, amalgamando diversos marcos teóricos dentro del marco de COMSOL. Al sincronizar la mecánica cuántica, los principios electromagnéticos y modelos basados en la física clásica, el estudio tiene como objetivo desentrañar la interacción entre la luz y el grafeno en estos dispositivos.
En su núcleo, este enfoque promete descubrir comportamientos matizados del grafeno dentro de sistemas plasmónicos. Al aprovechar la capacidad de simulación de COMSOL, desbloquea vías para optimizar diseños de dispositivos, impulsando aplicaciones en sensores de alto rendimiento, fotodetectores ultrarrápidos y dispositivos optoelectrónicos.
La integración de COMSOL en esta investigación no solo conecta aspectos teóricos con aplicaciones prácticas, sino que también impulsa el esfuerzo hacia aprovechar de manera más efectiva las capacidades del grafeno. Esto podría impactar en las telecomunicaciones, avanzar en la detección biomédica y mejorar las tecnologías de captación de energía.
La imagen de cabecera procede del modelo "Graphene Metamaterial Perfect Absorber", que se puede encontrar en la Application Gallery de COMSOL.