- Detalles
- Categoría: Minitab
- Visto: 9833
Un aspecto destacado de escribir y editar el blog de Minitab es la oportunidad de leer sus respuestas y responder a sus preguntas. A veces, para mi disgusto, nos indican que hemos cometido un error. Sin embargo, estoy particularmente agradecido por esos comentarios, ya que nos permite corregir errores involuntarios.
Pensé que tenía la oportunidad de corregir un error cuando vi que este comentario aparecía en una de nuestras publicaciones de blog más antiguas:
Usted dijo que un p-valor mayor que 0.05 da un buen ajuste. Sin embargo, en otra publicación, usted dijo que el p-valor debería estar por debajo de 0.05 si el resultado es significativo. ¡Por favor, míralo!
¿Alguna vez le han entrado escalofrios cuando se ha dado cuenta de que se ha equivocado? Eso es lo que sentí cuando leí ese comentario. Oh no, pensé. Si el p-valor es mayor que 0.05, los resultados de una prueba ciertamente no serían significativos. ¿Pasé por alto un error tan básico?
Antes de automachacarme, decidí revisar las publicaciones en cuestión. Después de revisarlas, me di cuenta de que no tendría que ponerme la camiseta después de todo. Pero la pregunta me recordó la importancia de una idea fundamental.
Comienza con la Hipótesis
Si en algún momento ha realizado un curso introductorio de estadística, probablemente recordará que el profesor le explicó a la clase lo importante que es formular sus hipótesis con claridad. Excelente consejo.
Sin embargo, muchas herramientas estadísticas comunmente utilizadas formulan sus hipótesis de forma que no coinciden. Eso es lo que este agudo comentarista notó y señaló.
El autor de la primera publicación detalló cómo usar Minitab para identificar la distribución de los datos, y en su ejemplo señaló que un p-valor mayor a 0.05 significaba que los datos se ajustaban a una distribución dada. El autor del segundo post, el suyo realmente, comentó la alarmante tendencia a utilizar un lenguaje engañoso para describir un alto p-valor como si indicara una significación estadística.
Para ponerlo en un lenguaje plano, el post de mi colega citaba el alto p-valor como un indicador de un resultado positivo. Y mi publicación reprendió a las personas que citan un alto p-valor como un indicador de un resultado positivo.
Ahora, ¿qué es lo que es tan confuso?
No olvidar lo que realmente se está comprobando
Puede ver dónde ésto parece una contradicción, pero para mi alivio, las publicaciones fueron consistentes. La aparición de la contradicción se deriva de las hipótesis discutidas en los dos mensajes. Vamos a verlo.
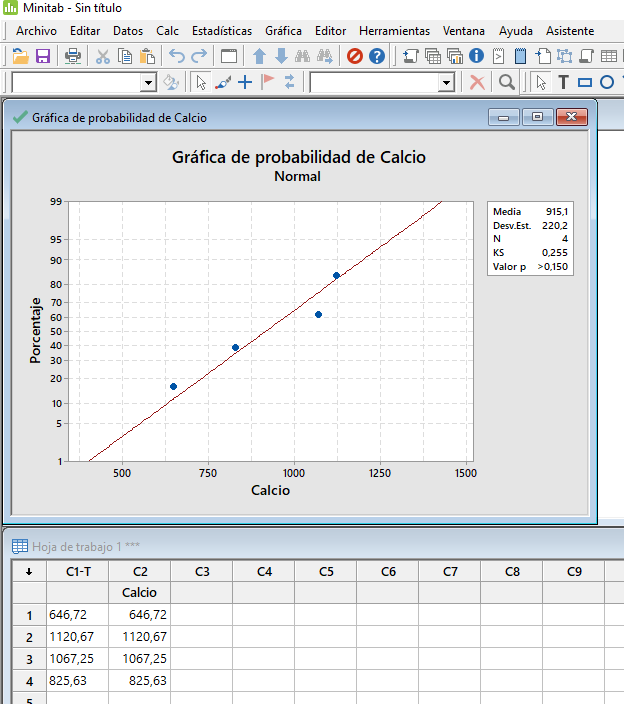
Mi colega presentó este gráfico, obtenido de la Identificación de Distribución Individual:
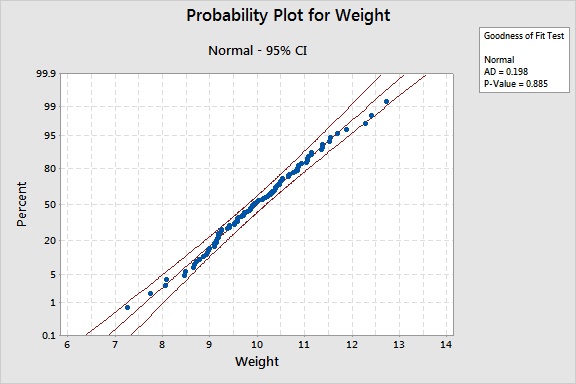
La identificación de distribución individual es un tipo de prueba de hipótesis, y por tanto el p-valor ayuda a determinar cuando se debe o no rechazar la hipótesis nula.
Aquí, la hipótesis nula es "Los datos siguen una distribución normal," y la hipótesis alternativa sería "Los datos NO siguen una distribución normal." Si el p-valor es mayor que 0.05, no podremos rechazar la hipótesis nula y concluiremos que los datos siguen la distribución normal.
Echemos un vistazo a ese p-valor:
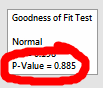
Es un p-valor alto. Y para esta prueba, eso significa que podemos concluir que la distribución normal se ajusta a los datos. Así que si estamos verificando la asunción de normalidad de estos datos, este alto p-valor es bueno.
Pero muy a menudo buscamos un p-valor bajo. En una prueba t, la hipótesis nula podría ser "las medias de la mustra NO SON diferentes," y la hipótesis alternativa, "Las medias de la muestra SON diferentes." Visto de esta manera, el valor o disposición de la hipótesis es opuesto al de la identificación de la distribución.
De ahí, la aparente contradicción. Pero en ambos casos un p-valor mayor que 0.05 significa que no podemos rechazar la hipótesis nula. Estamos interpretando el p-valor en cada prueba de la misma manera.
Sin embargo, como las connotaciones de "bueno" y "malo" son diferentes en los dos ejemplos, la manera de hablar sobre estos p-valores respectivos parecen contradictorios-hasta que consideramos exactamente lo que están diciendo la hipótesis nula y la alternativa.
Y ese es un punto importante que me alegra recordar.
- Detalles
- Categoría: Comsol
- Visto: 6352
Les invitamos a asistir a la conferencia COMSOL Conference 2019 para avanzar en sus conocimientos de simulación numérica y conectar con expertos en diseño y modelado como usted. Este evento se centra en la simulación multifísica y sus aplicaciones. Una gran variedad de sesiones le ofrecen de todo, desde ponencias principales inspiradoras dadas por líderes de la industria a discusiones cara a cara con ingenieros de aplicaciones y desarrolladores. Puede adaptar el programa a sus necesidades específicas, ya sea que su objetivo sea de aprendizaje de nuesvas técnicas de modelado o conectar con usuarios como usted del software COMSOL®. Únase a nosotros en la COMSOL Conference para:
- Permanecer al día de las herramientas y tecnologías de modelado multifísico actuales
- Seleccionar nuevas técnicas de simulación entre una variedad de minicursos y talleres
- Presentar un artículo o póster y ganar reconocimiento por su diseño y trabajo de investigación
- Interactuar con sus colegas en discusiones en paneles específicos de la industria
- Obtener asistencia en sus problemas de modelado en estaciones de demostración
- Aprender cómom construir y distribuir apliaciones de simulación para su equipo u organización
- Obtener inspiración de los líderes en simulación multifísica para su próximo diseño de innovación
SALA DE CONFERENCIAS
Churchill College, Universidad de Cambridge
Storey’s Way
Cambridge
CB3 0DS
Reino Unido
- Detalles
- Categoría: Minitab
- Visto: 631228
Una prueba de hipótesis es una regla que especifica cuando se puede aceptar o rechazar una afirmación sobre una población dependiendo de la evidencia proporcionada por una muestra de datos.
Una prueba de hipótesis examina dos hipótesis opuestas sobre una población: la hipótesis nula y la hipótesis alternativa. La hipótesis nula es la afirmación que se está comprobando. Normalmente la hipótesis nula es una afirmación de "sin efecto" o "sin diferencia". La hipótesis alternativa es la afirmación que se desea ser capaz de concluir que es verdadera basándose en la evidencia proporcionada por los datos de la muestra.
Basándose en los datos de la muestra, la prueba determina cuando rechazar la hipótesis nula. Se utiliza un p-valor, para realizar esa determinación. Si el p-valor es menos que el nivel de significación (conocido como α o alfa), entonces se puede rechazar la hipótesis nula.
Un error común suele ser que las pruebas de hipótesis estadísticas están diseñadas para seleccionar la más probable de dos hipótesis. Sin embargo, al diseñor una prueba de hipótesis, se configura la hipótesis nula como la que se quiere rechazar. Dado que se fija que el nivel de significación sea pequeño antes del análisis (normalmente, un valor de 0.05 funciona correctamente), Cuando se rechaza la hipótesis nula, se tiene una prueba estadística de que la alternativa es cierta. Por el contrario, si no se rechaza la hipóetesis nula, no se tiene prueba estadística de que la hipótesis nula sea cierta. Esto es debido a que no se ha fijado la probabilidad de que se acepte falsamente que la hipótesis nula sea pequeña.
Ejemplos de algunas preguntas que se pueden responder con una preuba de hipótesis:
- ¿La altura media de las mujeres en secundaria difiere de 168 cm?
- ¿La desviación estandar de sus alturas es igual o menor que 13 cm?
- ¿Los estudiantes masculinos y femeninos difieren en su altura promedio?
- ¿Es la proporción de estudiantes masculinos de secundaria significativamente más alta que la proporción de estudiantes femeninas de secundaria?
Ejemplo de realización de una prueba de hipótesis básica con Minitab
Se pueden seguir seis pasos básicos para configurar y realizar correctamente una prueba de hipótesis. Por ejemplo, el director de una fábrica de tuberías debe asegurarse de que los diámetros de sus tuberías sean igual a 5cm. El director sigue los siguientes pasos básicos para realizar el test de hipótesis.
NOTA
Se deberá determinar el criterio para la prueba y el tamaño de la muestra requerida antes de recoger los datos.
1. Especificar la hipótesis.
En primer lugar, el director formula la hipótesis. La hipótesis nula es: La media de la población de todas las tuberías es igual a 5 cm. Formalmente, esto se escribe: H0: μ = 5
Entonces, el director escoge entre las siguientes hipótesis alternativas:
Condición a prueba Hipótesis alternativa
La media poblacional es menor que el objetivo. unilateral: μ < 5
La media poblacional es mayor que el objetivo. unilateral: μ > 5
La media poblacional difiere del objetivo. a dos lados: μ ≠ 5
Como tienen que asegurarse de que las tuberías no sean mayores o menores a 5cm, el director elige la hipótesis alternativa de dos lados, que establece que la media de la población de todas las tuberías no es igual a 5cm. Formalmente se escribe como H1: μ ≠ 5
2. Escoger un nivel de significación (también llamado alfa o α).
El director selecciona un nivel de significación de 0.05, que es el más típico.
3. Recoger los datos.
Recogen una muestra de tubos y miden sus diámetros.
4. Comparar el p-valor de la prueba con el nivel de significación.
Después de realizar la prueba de hipótesis el director obtiene un p-valor de 0.004. El p-valor es menor que el nivel de significación de 0.05.
5. Decidir si rechazar o no rechazar la hipótesis nula.
El director rechaza la hipótesis nula y concluye que el diámetro medio de tubería de todas las tuberías no es igaual a 5cm.
Minitab Statistical Software dispone de múltiples pruebas de hipótesis que deben de utilizare según el tipo de datos y el objetivo.
- Detalles
- Categoría: Comsol
- Visto: 6239
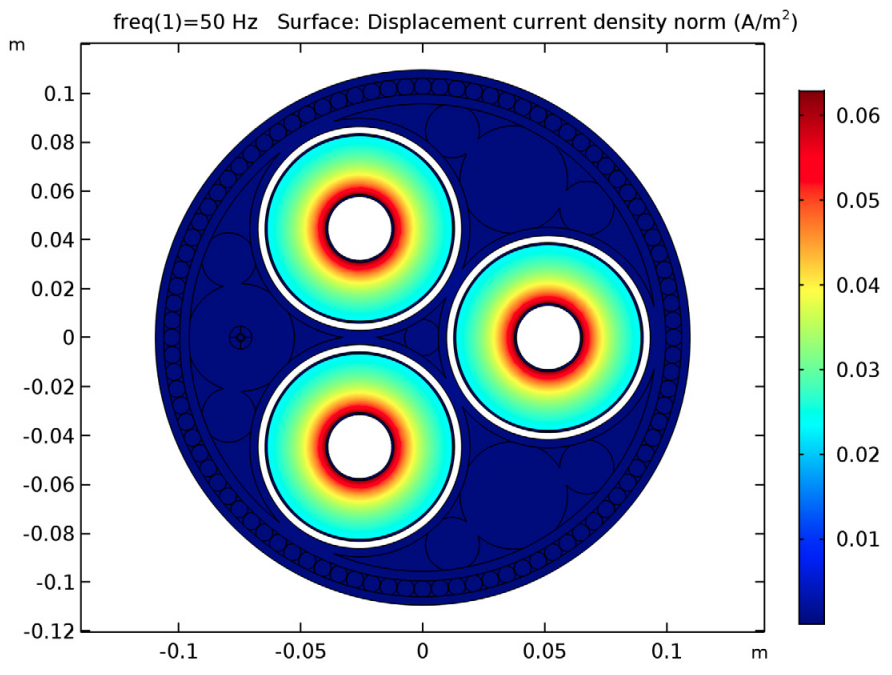
Los cables proporcionan energía a aviones a gran altura, en minas subterráneas y parques eólicos marinos. Dependiendo del tipo de uso, los cables pueden tener formas, tamaños y entornos muy diferentes, lo que afectará a su rendimiento. En su discurso de apertura en la Conferencia COMSOL 2018 de Lausana, Adrien Charmetant de Nexans explicó cómo se utiliza el modelado multifísico para optimizar los diseños de cables. En esta entrada del blog de COMSOL podrá encontrar un resumen de su conferencia y un video de su presentación.
Nexans es un proveedor global de soluciones de cable que ayuda a transmitir energía e información a millones de personas. Sus cables y accesorios se utilizan para presas hidroeléctricas, minas, parques eólicos marinos, centros de datos, rascacielos de las ciudades y transportes.
Para explicar el comportamiento acoplado de los cables, Charmetant y su equipo utilizan la simulación "como un complemento de los estándares". Señaló que el software COMSOL Multiphysics® los ayuda a resolver la física compleja con menos aproximaciones. "Permite un tiempo de comercialización más rápido y un desarrollo más barato de nuevos cables y nuevos accesorios", dijo Charmetant. Además, el modelado permite instalaciones de cable más seguras y con un costo optimizado, y ayuda a evitar el sobrecalentamiento. Otros beneficios incluyen la versatilidad de la simulación multifísica y la capacidad de llevar metodologías de diseño complejas a un público más amplio a través de aplicaciones de simulación.
Charmetant continuó discutiendo dos formas en que Nexans utiliza el modelado para mejorar el proceso de desarrollo de cables y sus accesorios: creación de prototipos virtuales, que agiliza el diseño de estos dispositivos, y el análisis dinámico, que ayuda a que la instalación de cables sea más rentable.
- Detalles
- Categoría: Maple
- Visto: 5500
Addlink Software Científico, distribuidor oficial del software de cálculo matemático Maple (Maplesoft) en España, estará presente en el Congreso Bienal de la Real Sociedad Matemática Española (RSME), que tendrá lugar en Santander, del 4 al 8 de febrero de 2019.
Además de disponer de un estand en la zona de exposición en el Aula 6 del Edificio Interfacultativo de la Facultad de Educación, el día 6 de febrero, el Dr. Jürgen Gerhard, Director Principal de Investigación de Maplesoft impartirá el seminario titulado "Special Functions in Maple".
Después de este seminario el Dr. Laureano González Vega, Catedrático de Álgebra de la Universidad de Cantabria, impartirá el Taller: "Matemáticas experimentales con Maple". El taller pretende proporcionar una primera toma de contacto en el uso de Maple como herramienta computacional para analizar la veracidad de afirmaciones matemáticas o, incluso, deducir nuevas afirmaciones.
- Detalles
- Categoría: Comsol
- Visto: 10729
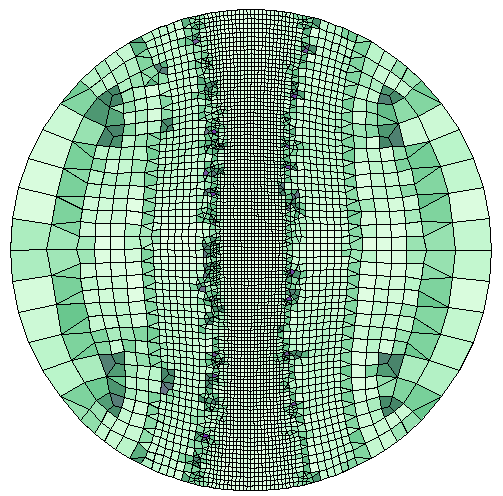
Erik Melin nos explica en su interesante artículo del blog de COMSOL cómo resolver los problemas de modelado FEM de una manera más eficiente, modificando la malla de forma adaptativa en COMSOL Multiphysics.
El objetivo de la adaptación de la malla es utilizar la menor cantidad de elementos posible para obtener una solución precisa. Por lo general es deseable utilizar una malla más gruesa en las regiones que no son muy importantes y una malla más refinada en las regiones de interés. Incluso se podría considerar el uso de elementos anisotrópicos. A partir de la versión 5.4 de COMSOL Multiphysics, éste incluye herramientas mejoradas para adaptar una malla. Esto es lo que nos explica Erik en esta entrada del blog.
Conocer el tamaño de su elemento de malla
Para adaptar una malla, es necesario proporcionar el tamaño del elemento deseado. Encontrar el tamaño correcto de los elementos no es una tarea sencilla. De hecho, está sujeta a mucha investigación. En COMSOL Multiphysics, puede usarse la funcionalidad de Adaptación y Estimaciones de Error en el estudio (para problemas estacionarios y valores propios) para adaptar automáticamente la malla en base a las estimaciones de error incorporadas.
La adaptación de malla en COMSOL Multiphysics, sin embargo, no está limitada al uso de estimaciones incluidas del error: es mucho más flexible. Es posible resolver un problema más simple en una malla gruesa y luego evaluar una expresión en esa solución para controlar el tamaño del elemento para el problema más avanzado. También se puede utilizar una función de interpolación importada o cualquier expresión que se pueda encontrar.
Esta publicación del blog de COMSOL no profundiza en este aspecto, sino que considera que el usuario, implícita o explícitamente, conoce el tamaño deseado del elemento como una función de x , y , y (en 3D) z. ¿Qué significa esto? La interpretación es que la longitud de un borde de un elemento de malla viene dada por la función evaluada en el punto medio de ese borde. Naturalmente, es (en general) imposible satisfacer exactamente este requisito. Incluso un solo triángulo necesita satisfacer la desigualdad del triángulo. Pero es importante tener en cuenta esta imagen: la expresión de tamaño representa la longitud del borde del elemento deseado en cada punto del espacio.
- Detalles
- Categoría: Comsol
- Visto: 4788
Todos los productos de COMSOL® han mejorado su estabilidad que se han introducido como actualizaciones. La siguiente lista contiene las mejoras más importantes de COMSOL® versión 5.4 update 2 (incluyendo las del update 1).
COMSOL Multiphysics®
- Solucionado un problema con un botón de radio que no respondía en el Model Builder para macOS.1
- Solucionado un problema donde las aplicaciones podían fallar al lanzarse en instancias de ejecución largas.2
- Mejorada la implementación de forma que las rutas de los archivos de informes proporcionados por el usuario durante las llamadas a métodos se almacenan en el modelo.2
- Mejoras de rendimiento para barridos paramétricos grandes.
- Solucionado un problema donde los recursos de archivos podían perderse al calcular en la ventana Test Application.2
- Se han realizado varias mejoras de estabilidad y rendimiento.1,2
COMSOL Server™
- Solucionado un problema con el instalador de COMSOL Server™ en versiones Windows® localizadas.1
- Solucionado un problema donde aplicaciones reemplazadas fallaban al lanzarse en servidores secundarios.2
- Implementoda una gestión más robusta de límites de tiempo de red en el lado servidor.2
COMSOL Compiler™
- Renombrado el botón Executable y la correspondiente ventana de Settings a Compiler.1
- Renombrado el botón Compile, utilizado para compilar aplicaciones, a Create Executable.1
AC/DC Module
- Añadido soporte de análisis de sensibilidad a la funcionalidad Terminal, aplicable a las interfaces Electric Currents, Electrostatics, Electrostatics, Boundary Elements, y Magnetic and Electric Fields.2
- Se han realizado varias mejoras de estabilidad.2
Acoustics Module
- Corregidas las variables de postprocesado globales generadas por la condición de Port en los modelos 2D axisimétricos.1
- Solucionado un problema cuando se utilizaba únicamente una frecuencia en un estudio junto con la funcionalidad de Port Sweep.1
CFD Module
- Correción de la densidad y viscosidad utilizadas para la condición de contorno Inlet en la interfaz Darcy's Law al utilizarla con el nodo de acoplamiento multifísico Multiphase Flow in Porous Media.1
- Corrección de la implementación para el uso de múltiples nodos Mass Source en la interfaz Phase Transport.1
- Realizas varias mejoras de estabilidad.2
Chemical Reaction Engineering Module
- Corregida la función de la tasa de capacidad calorífica (Cp/Cv) en la interfaz Thermodynamics.2
Composite Materials Module
- Solucionado un problema donde, en la interfaz Layered Shell, podían aparecer tensiones espúreas en elementos con grandes variaciones en la orientación normal. Este problema, que podía ocurrir para mallas importadas o junto con operaciones geométricas virtuales, ahora está solucionado.2
ECAD Import Module
- Mejorada la implementación de forma que las caras verticales ahora se incluyen en selecciones de red de contornos para capas de taladros en archivos ODB++.1
Heat Transfer Module
- Solucionada la definición del coeficiente de compresibilidad isobárica cuando se utiliza la densidad definida por el usuario.1
- Solucionado el soporte de malla móvil en las funcionalidades de cáscara.1
- Habilitado el acoplamiento multifísico Surface-to-Surface Radiation para las interfaces Slip Flow y High Mach Number Flow.1
- Corregida la expresión para Zmean (figura de mérito media) en el acoplamiento multifísico Thermoelectric Effect.1
- Solucionada la contribución de grosor fuera de plano a las funcionalidades de la interfaz de flujo de calor en geometrías 2D.1
- Corregida la definición de variables de postprocesado de flujo de calor difusivo cuando se utiliza el acoplamiento multifísico Heat Transfer with Radiative Beam in Absorbing Media.2
- Corregida la definición de temperatura ambiente en el nodo Ambient Thermal Properties cuando la lista de Temperature se pone a User-defined coefficient for deviation o User-defined correction.2
- Corrección de coeficientes de unos cuantos polinomios de Legendre de orden superior a 4.2
- Corregido el grosor fuera de plano a unidad y desactivadas las funcionalidades fuera de plano cuando está activo un acoplamiento multifísico que involucre una interfaz de radiación.2
- Solucionada la contribución del grosor fuera de plano para flujo no isotérmico turbulento con funciones pared o tratamiento de pared automático.2
- Corregida la funcionalidad de Opaque Surface para la interfaz Radiative Beam in Absorbing Media.2
- Solucionada la definición de densidad en el nodo Phase Change Material cuando se utiliza bajo la funcionalidad Solid con una malla móvil.2
- Eliminado el filtro de selección redundante en el conjunto de datos de postprocesado de un material en capas para obtener modelos más concisos.2
- Reemplado definido entre las subfuncionalidades Irreversible Transformation y Phase Change Material.2
- Solucionado un problema con la definición de la tasa de flujo de masa en la funcionalidad Interior Fan.2
- Corregida la definición de variables de postprocesado de balance de energía en casos con un acoplamiento multifísico que defina fuentes de calor en contornos.2
- Corregida la definición de la conductividad térmica en el nodo Phase Change Material cuando es utilizado bajo una funcionalidad Solid con una malla móvil.2
- Solucionado un problema de migración para modelos que contengan las interfaces Heat Transfer with Radiation in Participating Media construidas en las versiones 5.3a y anteriores.2
- Actualizada la definición de conductividad térmica cuando se especifican diferentes propiedades de material para el tejido dañado en la subfuncionalidad Thermal Damage.2
- Cancelada la contribución de trabajo realizada por cambios de presión para fllujo incompresible con aproximación Boussinesq para la interfaz Nonisothermal Flow.2
- Eliminada la posibilidad de definir un grosor fuera de plano en interfaces de transferencia de calor en geometrías 1D, 2D, y 2D axisimétrica cuando la transferencia de calor está acoplada con una interfaz de radiación.2
- Se ha añadido la visualización de la dirección de radiación en la funcionalidad Prescribed Radiosity.2
LiveLink™ for SOLIDWORKS®
- La interfaz LiveLink™ y el entorno de simulación de única ventana integrada ahora soporta SOLIDWORKS® 2019.1
Nonlinear Structural Materials Module
- Correción de un error en el modelo Souza-Auricchio para aleaciones con memoria de forma.1
- Corrección de un problema cuando se creaba una ley de deslizamiento definida por el usuario utilizando un Potential en el nodo Creep. En versiones anteriores, se aplicaba un factor de dos en los téminos fuera de la diagonal en la expresión de potencial para tener en cuenta la simetría en el tensor de tensión. Este factor se basaba en la asunción de que la expresión del potencial se escribió en términos de únicamente las partes superiores a la diagonal del tensor de tensión. Con esta actualización, el potencial se considera que está escrito en una forma estándar, de forma que las tasas de deformación de cizalladura se calculan directamente como la derivada del potencial respecto al elemento tensor de tensión correspondiente.1
Particle Tracing Module
- Las funcionalidades de Heat Source, Convective Heat Losses, y Radiative Heat Losses para la interfaz Particle Tracing for Fluid Flow ahora respetan las selecciones de dominio.1
- Mejora del manejo de dispersión difusa o emisión de partículas o rayos desde contornos interiores.2
- Corregido el coeficiente en la fuerza de elevación Saffman para tener en cuenta una corrección al papel Saffman original.2
- Añadidas variables dependientes auxiliares en partículas al menú Add/Replace Expression durante el procesado de resultados.2
Pipe Flow Module
- Las funcionalidades de Pipe Connection en modelos antiguos que uitlizan la interfaz Nonisothermal Pipe Flow tal cual, con un aviso de que la funcionalidad está obsoleta y que se eliminará en versiones futuras.1
Plasma Module
- Cambiada la funcionalidad de forma que la interfaz Boltzmann Equation, Two-Term Approximation ahora está disponible en componentes 0D. La versión anterior, que estába disponible en 1D, ahora se ha retirado. Los modelos existente que utilizaban la versión 1D de la interfaz todavía pueden ser abiertos y modificados.2
Ray Optics Module
- Salvaguarda adicional contra errores por divisiones por cero al utilizar la funcionalidad Ray Termination.1
- Mejorada la funcionalidad para configurar automáticamente la entrada del modelo de frecuencia para índices refractivos que dependan de la frecuencia o longitud de onda del rayo. Si se había configurado la entrada del modelo previamente de forma manual, por ejemplo a comp1.gop.f0, entonces, después de la actualización, hay que ir a Common Model Inputs, hacer clic derecho en Frequency (Hz) -minput.freq y escoger Reset to Default.1
Semiconductor Module
- Corrección de la visualización de la ecuación de Poisson en la interfaz Semiconductor.1
Structural Mechanics Module
- Corrección de un error que podía ocurrir al añadir Adhesion en una interfaz Solid Mechanics que todavía contenga el nodo Plasticity.1
- Corrección de un error que podía ocurrir al utilizar Compact History en un modelo que contenga un acoplamiento multifísico Solid-Beam Connection.1
- Mejora en el rendiimiento para postprocesado con conjuntos de datos Shell.2
- Corregido un error que ocurría durante la generación de secuencias del resolvedor por defecto para modelos multifísicos que contenían un nodo Damage en la interfaz Solid Mechanics.2
- Incluidas pérdidas desde la funcionalidad Thin-Film Damping al calcular la disipación de potencia y el factor de calidad en la interfaz Solid Mechanics.2
- Se han realizado mejoras de estabilidad.2
Subsurface Flow Module
- Corrección en la definición de la formulación de la Permeabilidad y Kozeny-Carman para la ecuación de Richards para utilizar la permeabilidad relativa para calcular la transmisibilidad.1
- corregida la contribución de velocidad debida a la gravedad con aceleración especificada para la funcionalidad Fracture Flow.2
1Nuevo en update 1
2Nuevo en update 2