Detalles

Categoría: Maple

Publicado: 28 Mayo 2021

Visto: 3227

• actualización
• soporte técnico
• Maple Flow
• Maple Flow 2021

Maple Flow 2021.1 es una actualización importante de Maple Flow 2021. Está disponible para todos los usuarios de Maple Flow 2021.

Esta actualización contiene las siguientes adiciones y mejoras:

• Imprimir/exportar a pdf
  • Defina el tamaño de página (por ejemplo, carta, A4, etc.) y márgenes
  • Definir encabezados/pies de página para la página impresa/exportar PDF
  • Mostrar la extensión de la página en el lienzo
• Conjuntos de estilo
  • Soporte para estilos de texto/matemáticas
  • Cambiar estilos con conjuntos de estilos basados ​​en Maple
• Modos de cálculo numérico/simbólico separados
  • Modo de evaluación "simbólico" adicional que suprime la evaluación numérica tanto como sea posible<7li>
  • El modo de evaluación simbólico se puede hacer "pegajoso" (es decir, todos los contenedores matemáticos futuros serán simbólicos si se establece el modo simbólico fijo)
• Soporte de idioma japonés
• Otras mejoras de la interfaz y correcciones de errores

Detalles

Categoría: Maple

Publicado: 28 Mayo 2021

Visto: 3368

Maple 2021.1 es una actualización de mantenimiento de Maple 2021. Contiene una serie de correcciones y mejoras a Maple 2021, en una variedad de áreas, que incluyen:

• Mejoras en el trazado de gráficas, incluida la corrección de un problema en el que la barra de herramientas de graficado a veces no aparecía.
• Mejoras en la exportación de PDF y LaTeX, incluida la solución de un problema por el que las anotaciones de gráficos se movían o desaparecían en la exportación de PDF
• Problemas resueltos relacionados con guardar y eliminar carpetas de libros de trabajo
• Se han añadido nuevas opciones para dividir y unir bloques de documentos
• Restaurada la paleta de reconocimiento de escritura a mano
• Se cambió la ubicación para almacenar archivos de respaldo en la carpeta de inicio del usuario.
• Mejoras en soluciones completas y paso a paso
• Correcciones a cuadros de texto y componentes de entrada matemática.
• Mejoras en el panel de contexto
• Solucionado un problema en la teoría de grafos que podía hacer que Maple se bloqueara
• Actualizaciones de las páginas de ayuda, incluidas mejoras en la documentación del paquete de física.
• Problema corregido con ThermophysicalData: -Atmosphere
• Soporte para MapleSim 2021 y Maple Flow 2021.1

Obtener la actualización
En el menú Herramientas en Maple 2021, seleccione Buscar actualizaciones y siga las instrucciones.
Si esa opción está deshabilitada, puede descargar la actualización haciendo clic en el enlace inferior.

Nota para los usuarios de MapleSim: esta actualización de Maple se instalará automáticamente cuando instale MapleSim 2021.

Detalles

Categoría: MapleSim

Publicado: 27 Mayo 2021

Visto: 4131

Maplesoft acaba de anunciar sus nuevas soluciones llave en mano para fabricantes de máquinas que hacen que la puesta en servicio virtual sea altamente accesible incluso para organizaciones que no tienen experiencia en modelado y simulación utilizando gemelos digitales. Al proporcionar una combinación de productos y servicios de ingeniería, Maplesoft trabajará en estrecha colaboración con organizaciones que son nuevas en la puesta en marcha virtual para identificar un proyecto adecuado, desarrollar un modelo virtual de alta fidelidad e implementar ese modelo para cualquier persona de la organización que lo necesite utilizando MapleSim Insight. una plataforma de simulación simple pero potente. La última versión de MapleSim Insight proporciona capacidades mejoradas de depuración y visualización en 3D basadas en simulación que se conectan directamente a plataformas de automatización comunes.

Durante más de 10 años, Maplesoft ha proporcionado a los ingenieros herramientas de modelado y simulación para un desarrollo de productos más rápido y rentable. Al adoptar un enfoque de simulación basado en modelos, las empresas pueden resolver problemas de rendimiento de la máquina al diagnosticar las causas raíz de los problemas que de otra manera serían muy difíciles de identificar. Sin embargo, la construcción de gemelos digitales basados ​​en modelos es un nuevo conjunto de capacidades de la ingeniería que muchas empresas aún tienen que desarrollar, lo que les impide aprovechar los beneficios de esta nueva tecnología.

Para abordar estos problemas, Maplesoft ofrece ahora nuevas soluciones llave en mano para crear gemelos digitales e implementar la puesta en servicio virtual. Maplesoft ofrece a los clientes soluciones de servicio completo para diagnosticar, reparar y optimizar el rendimiento de la máquina. Los clientes pueden buscar soluciones a problemas individuales sin tener experiencia previa en simulación, y Maplesoft proporcionará un gemelo digital validado que puede producir resultados poderosos y económicos. Estos gemelos digitales se desarrollan utilizando MapleSim, la herramienta de simulación y modelado multidominio de Maplesoft, que proporciona un entorno único para modelar todos los sistemas clave que se encuentran en los diseños típicos de máquinas, incluidos los sistemas mecánicos, hidráulicos y eléctricos.

Los clientes también reciben una nueva versión de MapleSim Insight, que es una herramienta de bajo coste para simular, visualizar y compartir modelos de MapleSim con equipos que aún no están familiarizados con las herramientas de modelado. En 2021, MapleSim Insight ofrece a los usuarios resultados de simulación más rápidos, más opciones para el trazado 2-D y visualizaciones 3-D, y capacidades mejoradas para análisis personalizados en profundidad. Los clientes también pueden usar MapleSim Insight para la visualización y prueba en tiempo real del código de control de la máquina, con opciones de conectividad directa para herramientas de automatización estándar de la industria. Las mismas visualizaciones 3D también pueden ser utilizadas por personas no expertas, como equipos de ventas que buscan proporcionar demostraciones de hardware personalizado a nuevos clientes.

"La mayoría de las empresas ya comprenden que pueden ahorrar tiempo y dinero a largo plazo si utilizan gemelos digitales en el desarrollo de sus productos", afirma Chris Harduwar, vicepresidente de desarrollo empresarial de Maplesoft. “Sin embargo, lo que les impide seguir adelante es el esfuerzo que se necesita para comenzar. Aprender a construir un modelo es una gran inversión a corto plazo, que puede ser difícil de justificar cuando todos están ocupados y no está seguro de qué tan bien los beneficios teóricos se traducirán en ventajas concretas en su propio contexto específico. Las soluciones llave en mano de Maplesoft brindan a las empresas una forma de poco esfuerzo para descubrir cómo los gemelos digitales y la puesta en servicio virtual pueden ayudarlas a resolver sus problemas prácticos inmediatos, y nadie tiene que aprender a construir modelos a menos que lo desee ".

Las nuevas soluciones llave en mano de Maplesoft ahora están disponibles junto con las nuevas versiones de MapleSim y MapleSim Insight. La familia de productos MapleSim 2021 permite a los ingenieros abordar problemas de diseño más fácilmente que nunca, con un rendimiento de simulación mejorado y visualizaciones en 3-D, nuevas formas de compartir modelos con quienes no usan MapleSim y una gran cantidad de bibliotecas de componentes nuevas y ampliadas. .

Detalles

Categoría: Minitab

Publicado: 25 Mayo 2021

Visto: 3135

• Minitab Statistical Software
• Control de llenado

Durante más de 50 años, USC Consulting Group (USCCG) ha estado impulsando la excelencia operativa con la misión de proporcionar valor real mediante la mejora del rendimiento financiero. USCCG ayuda a las empresas a alcanzar su máximo potencial al mejorar los procesos y operaciones en toda la cadena de suministro. Las soluciones de Minitab brindan una ayuda esencial a USCCG en sus esfuerzos por resolver los problemas a los que se enfrentan sus clientes, y siguen siendo un componente clave para que sus operaciones sigan funcionando a niveles óptimos. 

El desafío

Si su negocio es el envasado, usted sabe lo importante que es controlar los procesos de llenado. El llenado excesivo tiene el mismo efecto neto que regalar dinero a sus clientes. En las operaciones de alto volumen, esto puede sumar fácilmente cientos de miles de dólares cada año. Por otro lado, si el llenado es insuficiente, las multas y el daño a su reputación pueden ser aún más costosos.

Al llenar envases, el primer requisito es cumplir con las regulaciones gubernamentales en cuanto al contenido neto declarado en los productos envasados. En pocas palabras, el peso unitario de llenado debe estar por encima de un mínimo especificado, de acuerdo con la varianza máxima permitida (MAV en inglés). Su peso promedio de llenado debe estar en o por encima, nunca por debajo, de lo indicado en la etiqueta.

Muchas empresas hoy en día creen que el llenado excesivo es la única manera de evitar multas reglamentarias y mantener la lealtad de los clientes. Por lo tanto, su objetivo es acercarse tanto como sea posible al peso declarado en el envase, sin llegar a quedar por debajo. Eso parece ser perfectamente razonable, pero muchas empresas tienen dificultades para lograr este objetivo. ¿Será porque no entienden plenamente las capacidades de sus procesos? ¿O será que no han adoptado las herramientas y técnicas correctas, como Manufactura esbelta, Six Sigma o tecnología, para reducir la variación y controlar los procesos? Tal vez simplemente sea una cuestión de ejecución. La respuesta puede ser cualquiera de las anteriores o todas ellas.

Minimizar y controlar la variación en el peso de llenado y usar técnicas de modelado estadístico puede redirigir una cantidad considerable de dinero a su balance final. Minitab es la solución ideal para optimizar el peso de llenado y ha ayudado a muchos clientes, en una variedad de industrias, a reducir millones de dólares de llenado excesivo.

Cómo ayudó Minitab

Cuando USCCG analizó estadísticamente los pesos de llenado de unos envases de gominolas de un importante fabricante de golosinas, determinó que el promedio de los pesos reales de llenado por SKU estaba hasta un 7% por encima de lo indicado en la etiqueta. Sin embargo, fijarse solamente en los promedios puede ser muy engañoso, ya que la variación en el peso de llenado puede arruinar fácilmente la oportunidad de recuperar cualquier llenado excesivo.

Al observar el proceso de llenado, USCCG también se dio cuenta de que los operadores estaban actuando en respuesta a comentarios sobre mediciones del peso de llenado e interfiriendo con los procesos en lugar de determinar las verdaderas fuentes de variación y tomar medidas correctivas permanentes. Ese era un factor que contribuía a la alta variación del proceso en relación con la variación en el peso de llenado. Saber cuándo dejar que el proceso continúe ejecutándose o cuándo hacer ajustes en el peso de llenado resulta primordial. Era evidente la necesidad de contar con gráficas de control estadístico de procesos (CEP) por línea y por producto.

Utilizando Minitab Statistical Software, la capacidad general del proceso se examinó primero tanto por línea como por SKU, en referencia a los pesos declarados en la etiqueta y las varianzas máximas permitidas (MAV). Los resultados revelaron que el proceso era propenso al llenado excesivo. Con la orientación de USCCG, el fabricante pudo entonces minimizar tanto la variación como el llenado excesivo utilizando una gráfica de control Xbar/R.   

La figura 1, abajo, muestra un ejemplo de la capacidad general de los pesos de llenado para un tarro de gominolas en cuya etiqueta se afirma que pesa 2268 g. El límite de especificación inferior (LSL) es 2205 g basado en la MAV. Los datos se transformaron utilizando la transformación de Johnson para que se ajustaran a una distribución normal. 

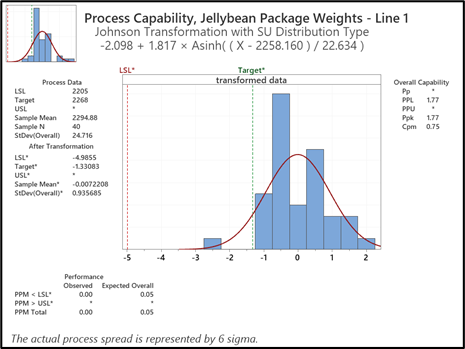
Figura 1: Capacidad general de un proceso de llenado de tarros de gominolas: Objetivo (indicado en la etiqueta) = 2268 g, Llenado promedio = 2294.88 y un LSL = 2205 g.

Como se ve en la figura 1, el peso promedio de llenado de 2294.8 g está más de 26 g por encima de lo indicado en la etiqueta y la cantidad esperada de unidades <LSL es mínima. El modelado adicional (figura 2) sugiere que un desplazamiento de 26 g para reducir los pesos de llenado da como resultado un peso promedio de llenado de 2268.88 g. Además, el Cpm aumentó de 0.75 a 1.46. También en este caso, el modelo muestra una cantidad mínima de unidades por debajo del LSL. Cabe señalar que todas las líneas de proceso cuentan con balanzas de verificación provistas de un mecanismo de rechazo para asegurar que los tarros no se despachen por debajo de la MAV.

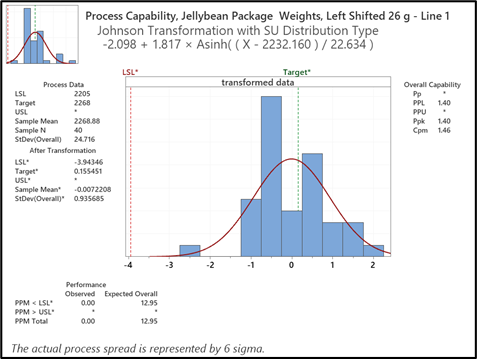
Figura 2: El modelo de capacidad general de un peso de llenado de gominolas desplazado en 26 g para reducir los pesos de llenado muestra una cantidad mínima de pesos unitarios por debajo del LSL y con un peso promedio de llenado de 2268.88 g.

Puesto que el peso promedio del envase cumple con lo indicado en la etiqueta y que el modelo proyecta una mínima cantidad de unidades MAV, se descartarán aproximadamente 13 en las balanzas de verificación de las líneas y se cumplirá con ambas regulaciones gubernamentales en cuanto a lo declarado en las etiquetas. USCCG ahora puede crear una gráfica Xbar/R (figura 3) y utilizar estos límites de control como punto de partida no solo para ayudar a mantener la línea central según lo estimado por el modelo de capacidad general, sino también para reducir aún más la variación en el peso. Esto, a su vez, podría permitir reducir aún más las unidades MAV o eliminarlas por completo.

Muchas organizaciones se esfuerzan por encontrar un equilibrio entre la reducción del llenado excesivo y los rechazos debido a violaciones de la MAV. Por ejemplo, si la línea central que se muestra en nuestro modelo de capacidad generara un alto número de violaciones de MAV (inaceptables para muchas operaciones de llenado), uno podría verse obligado a elevar más el promedio (línea central) para reducir el número de rechazos por MAV. El compromiso es más llenado excesivo a cambio de menos retrabajo: la actividad de abrir los envases rechazados y volver a introducir el material en la corriente de valor. La clave es utilizar la gráfica Xbar/R para reducir la variación en el peso de llenado, mantener las líneas centrales y evitar el retrabajo debido a las unidades rechazadas. 

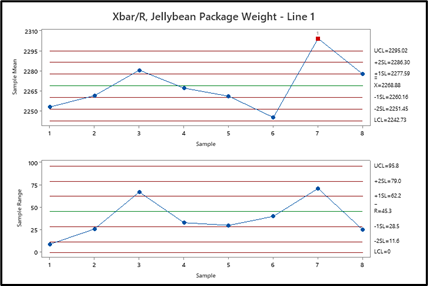
Figura 3: Gráfica Xbar/R mostrando la línea central y los límites de control correspondientes que se deben utilizar de acuerdo con el modelo de capacidad general.

Las líneas centrales y los límites de control estimados nunca deben considerarse valores absolutos, y es necesario probarlos en la práctica. Por lo tanto, las gráficas de control deben implementarse utilizando 4 pasos principales:

1. Si no se entiende claramente, determine la relación entre las entradas y las salidas para asegurarse de que se entiendan bien los efectos del ajuste del proceso. Esto permite a los operadores reaccionar de manera efectiva cuando el proceso está fuera de control y centrar el proceso rápidamente. Este paso también ayuda a calificar los límites de control que se han estimado.
2. Utilice las reglas para probar las gráficas de control: las reglas de Western Electric y las relaciones establecidas en el primer paso para verificar que el proceso se puede mantener bajo control y que se logra el peso promedio de llenado (línea central).
3. Instruya a los operadores y al personal necesario en cuanto a los beneficios y el uso de las gráficas de control antes de la implementación. Se recomienda entrenar y asesorar a los operadores en las líneas de proceso durante la elaboración de las gráficas. Además, cree un proceso diario de revisión de gráficas para garantizar que: (1) las gráficas se utilicen correctamente, (2) se alcance la línea central de la gráfica, (3) haya muy pocas o ninguna violación de la MAV y (4) se identifique cualquier causa especial y se actúe en consecuencia.
4. Revise periódicamente si la variación ha disminuido y si es necesario volver a calcular los límites de control. Continuar con el análisis de capacidad general también ayudará a establecer nuevas líneas centrales.  

Debe quedar claro que, aunque ayuda en gran medida a reducir el llenado excesivo, aplicar los métodos de análisis de capacidad y control estadístico de procesos no es toda la solución. Para acceder a todo el beneficio, también se deben aplicar herramientas, técnicas y métodos de manufactura esbelta como ayuda para mejorar el flujo continuo de materiales, aumentar el tiempo de actividad de los equipos y reducir el tiempo de transición. El esfuerzo combinado se traducirá en ahorros significativos en materiales y un mayor rendimiento.

Resultados

Los números lo demuestran. El llenado excesivo de las golosinas envasadas se redujo en más de un  50%, lo que se tradujo en más de $1.2 millones en ahorros anuales en materiales. ¡Eso sí que es dulce! 

Sobre el autor invitado

El Dr. Frank J. Esposto dirige el centro de calidad de USCCG y lleva con la empresa más de 18 años. Como director senior de Calidad y como master black-belt en Six Sigma Esbelto, el Dr. Esposto es responsable de organizar y dirigir los esfuerzos de Manufactura esbelta/Six Sigma para el diverso grupo de clientes de USCCG. Ha trabajado con clientes en muchas industrias para resolver problemas de productividad/calidad, personalizando y ofreciendo soluciones y enfoques para resolver problemas, diferentes tipos de cursos sobre cómo resolver problemas o resolviendo problemas específicos cuando los clientes no cuentan con las competencias esenciales. El Dr. Esposto también ha impartido capacitación en los niveles black-belt y green-belt en numerosas industrias, donde ha implementado iniciativas de Six Sigma en combinación con Manufactura esbelta.

Detalles

Categoría: Lakes

Publicado: 20 Mayo 2021

Visto: 4210

El pasado 11 de este mes la US EPA anunció revisiones de su modelo de dispersión del aire AERMO, AERMET - el preprocesador de datos metereológicos del sistema AERMOD- y AERSCREEN. Los ejecutables del modelo actualizado han sido publicados en el sitio web SCRAM.

En estas páginas web pueden encontrarse las listas de cambios para cada modelo AERMOD, AERMET, y AERSCREEN. Los cambios significativos incluyen:

• Nuevas opciones del modelo no predeterminado (ALPHA) que incluyen:
  •     2 nuevos métodos de conversión NO2 (Generic Reaction Set Method & Travel Time Reaction Method)
  •     Ajustes A&WMA descendentes
  •     Modificaciones de viento bajo
• Adición de una segunda barrera con el tipo de fuente RLINEXT y mejoras de velocidad a los algoritmos de fuente RLINE/RLINEXT
• Opción para ignorar los valores de turbulencia específicos del lugar del archivo de Perfil meteorológico (*.PFL)
• Nueva función de agrupamiento para fuentes lineales boyantes
• Correción de errores en los tres modelos, ¡y más!

El equipo de Lakes Environmental está trabajando rápidamente para implementar estas actualizaciones en AERMOD View, AERMET View, la versión paralela de AERMOD (AERMOD MPI), y AERSCREEN View para incorporar los cambios del Modelo Version 21112.

Detalles

Categoría: Minitab

Publicado: 10 Mayo 2021

Visto: 19505

• Minitab
• Diseño de Experimentos (DOE)
• alimentación
• estadística
• Food & Beverage

Como persona a la que le encanta cocinar (y comer) pasteles, me resulta molesto pasar por todo el esfuerzo de hornear el pastel y que el resultado final quede demasiado seco. Por esa razón, decidí utilizar un diseño de experimentos en Minitab para que me ayudara a reducir la pérdida de humedad en el horneado de los pasteles de chocolate y encontrar la configuración óptima de mis factores de entrada para producir un pastel de chocolate esponjoso. Comparto los detalles del diseño y los resultados en esta publicación.

ELECCIÓN DE FACTORES DE ENTRADA PARA EL DISEÑO DEL EXPERIMENTO

Como me gusta utilizar mezclas de pastel de chocolate prefabricadas, decidí usar dos de mis marcas de mezcla de pastel favoritas para el experimento. En esta publicación, llamaré a las marcas A y B. Pensando en los factores que podrían afectar a la pérdida de humedad, es probable que el tiempo de horneado y la temperatura del horno afecten a los resultados. Por lo tanto, los factores o entradas que decidí usar para el experimento son:

1. Marca de la mezcla para pasteles: A o B (datos categóricos)
2. Temperatura del horno: 350 o 380 grados Fahrenheit (datos continuos)
3. Tiempo de cocción: 38 o 46 minutos (datos continuos)

MEDIDA DE LA RESPUESTA

A continuación, necesitaba una forma de medir la pérdida de humedad. Para este experimento, utilicé una balanza de alimentos electrónica para pesar cada pastel (en la misma bandeja para hornear) antes y después de hornear, y luego usé esos pesos junto con la fórmula siguiente para calcular el porcentaje de humedad perdido para cada pastel:

%Pérdida de humedad = 100 x (peso inicial - peso final peso)/peso inicial

DISEÑO DEL EXPERIMENTO

Para este experimento, decidí construir un diseño factorial completo de 2³ con puntos centrales para detectar cualquier posible curvatura en la superficie de respuesta. Dado que la marca de la mezcla para pasteles es categórica y, por lo tanto, no tiene un punto central entre la marca A y la marca B, el número de puntos centrales se duplicará para ese factor. Por eso, tendré que hornear 10 pasteles que, incluso para mí, son demasiados en un solo día. Por lo tanto, decidí realizar el experimento durante dos días. Debido a que las diferencias entre los días en los que se recopilaron los datos podrían introducir variaciones adicionales, decidí agregar un bloque al diseño para tener en cuenta cualquier variación potencial debido al día.

Para crear el diseño en Minitab, se utiliza Estadísticas>DOE> Factorial>Crear diseño factorial:

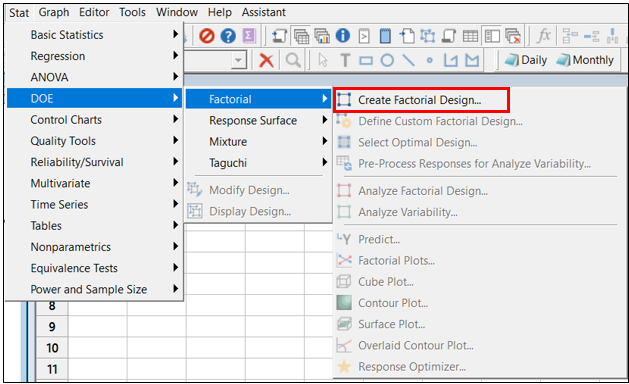
Minitab facilita la introducción de los detalles del diseño. Primero, se selecciona 3 como el número de factores:

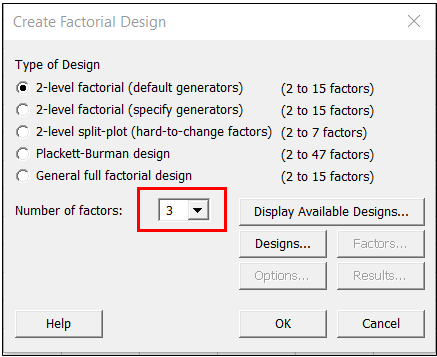
A continuación, se hace clic en el botón Diseños de arriba. En la ventana Diseños, puede decirse a Minitab qué tipo de diseño se deseará utilizar con los 3 factores:

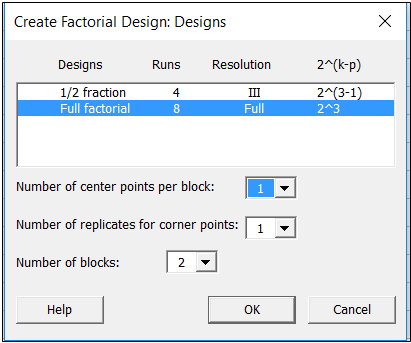
En la ventana anterior, se seleccionó un diseño completo de 2³ y también se añadieron 2 bloques (para tener en cuenta la variación entre días) y 1 punto central por bloque. Después de hacer las selecciones y hacer clic en Aceptar en la ventana anterior, se hizo clic en el botón Factores en la ventana principal para introducir los detalles sobre cada uno de los factores:

Debido a que los puntos centrales se duplican para factores categóricos, y debido a que este diseño tiene dos bloques, el diseño final tendrá un total de 4 puntos centrales. Después de hacer clic en Aceptar en la ventana de arriba, se terminó con el diseño que se muestra a continuación con 12 ejecuciones:

REALIZAR EL EXPERIMENTO Y ANALIZAR LOS DATOS

Después de pasar un fin de semana entero horneando pasteles y calcular la pérdida de humedad para cada uno, ingresé los datos en Minitab para el análisis. ¡También traje mucho pastel para compartir con mis colegas de Minitab!

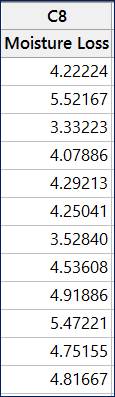
Con la pérdida de humedad de cada uno de mis 12 pasteles registrada en la columna C8 en la hoja de trabajo del experimento, se está dispuesto a analizar los resultados.

En Minitab, se utiliza Estadísticas>DOE>Factorial> Analizar diseño factorial... y luego se introduce la columna de "Pérdida de humedad" en el campo Respuestas:

En la ventana de arriba, también se hace clic en Términos para asegurarse de que solo se incluyen los efectos principales y las interacciones bidireccionales. Después de hacer clic en Aceptar en cada ventana, Minitab produce una gráfica de Pareto de los efectos estandarizados que puede utilizarse para reducir mi modelo:

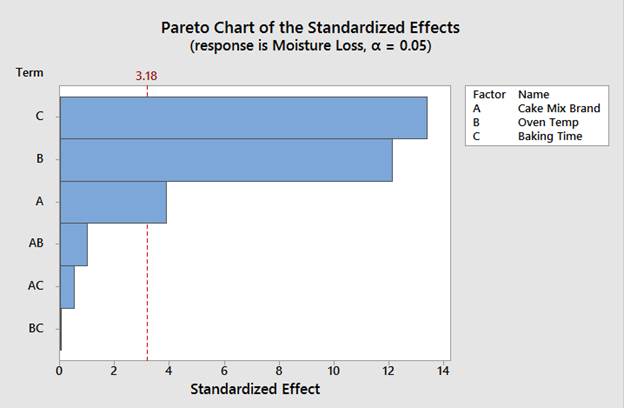
En el gráfico anterior puede verse que los efectos principales (A, B y C) tienen un impacto significativo en la humedad del pastel, ya que las barras que representan esos términos en el gráfico se extienden más allá de la línea de referencia vertical roja. Todas las interacciones bidireccionales (AB, AC y BC) no son significativas.

También puede verse la misma información en la tabla ANOVA en la ventana de sesión de Minitab:

En la tabla ANOVA anterior, se puede ver que la marca de la mezcla para pastel, la temperatura del horno y el tiempo de horneado son significativos ya que sus valores p son más bajos que mi alfa de 0.05.

También podemos ver que todas las interacciones bidireccionales tienen valores p superiores a 0,05, por lo que se concluye que esas interacciones no son significativas y deben eliminarse del modelo.

Curiosamente, el valor p de los bloques es significativo (con un valor p de 0,01). Esto indica que efectivamente hubo una diferencia entre los dos días en los que se recopilaron los datos que afectó los resultados. ¡Me alegra haber tenido en cuenta esa variación adicional al incluir un bloque en mi diseño!

ANÁLISIS DEL MODELO REDUCIDO

Para analizar el modelo reducido, puede volverse a Estadísticas>DOE>Factorial>Analizar diseño factorial. Esta vez, cuando se hace clic en el botón Términos, se consevan solo los efectos principales y se eliminan las interacciones bidireccionales. Minitab muestra la siguiente tabla ANOVA para el modelo reducido:

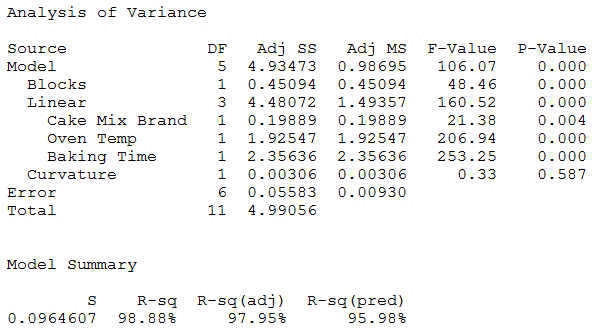
La tabla muestra que todos los términos que se han incluido (marca de mezcla, temperatura del horno y tiempo de horneado) son significativos, ya que todos los valores p para estos términos son inferiores a 0,05. También podemos ver que la prueba de curvatura basada en los puntos centrales no es significativa (valor p = 0,587), por lo que podemos concluir que la relación entre los tres factores y la pérdida de humedad es lineal.

Los valores de r cuadrado, r cuadrado ajustado y r cuadrado predicho son bastante altos, por lo que este modelo parece ajustarse muy bien a los datos.

COMPROBACIÓN DE LOS RESIDUOS

Ahora se puede echar un vistazo a los gráficos residuales para asegurarse de que se hayan cumplido todas las suposiciones del modelo para el modelo:

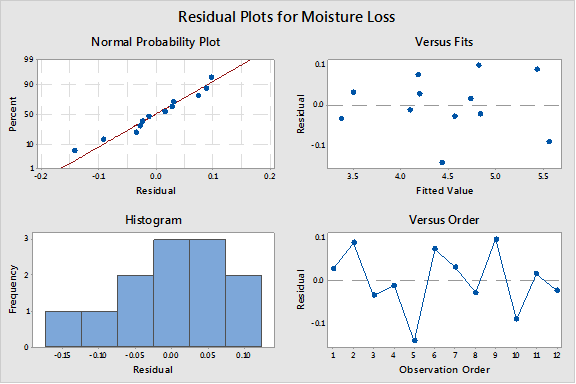
Los residuos del gráfico anterior parecen estar distribuidos normalmente. El gráfico de residuos versus ajustes parece mostrar que los puntos están dispersos aleatoriamente por encima y por debajo de 0 (lo que indica una varianza constante), y el gráfico de residuos versus orden no sugiere ningún patrón que pueda deberse al orden en el que se recopilaron los datos.

Ahora que se está seguro de que se han cumplido las suposiciones para el modelo, se puede utilizar este modelo para determinar la configuración óptima de los factores para que, en el futuro, todos los pasteles que se hagan estén húmedos y fabulosos.

OPTIMIZACIÓN DE LA RESPUESTA

Puede utilizarse el Optimizador de respuesta de Minitab y el modelo para que diga exactamente qué combinación de marca de mezcla para pastel, temperatura del horno y tiempo de horneado se desea utilizar para obtener el pastel más jugoso. Se selecciona Estadísticas>DOE>Factorial>Optimizador de respuesta:

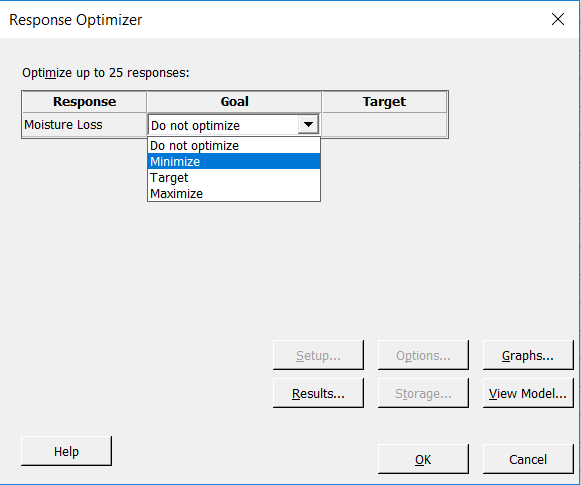
En la ventana anterior, puedo decirse a Minitab cuál es el objetivo. En este caso, se quiere saber qué configuraciones de entrada utilizar para minimizar la pérdida de humedad. Por lo tanto, se escoge Minimizar en la ventana de arriba y luego se hace clic en Aceptar:

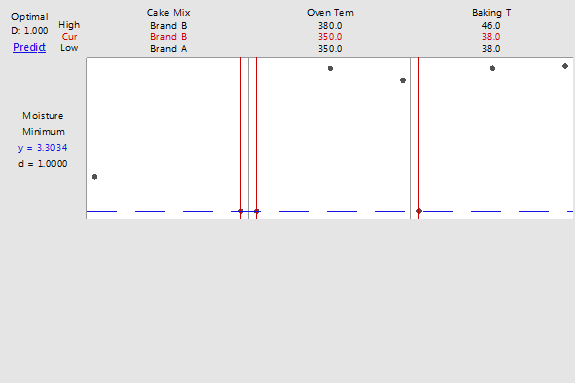
En el gráfico anterior, las configuraciones óptimas para los factores están marcadas en rojo cerca de la parte superior. Utilizando el modelo que se ajustó a los datos, Minitab dice que puede utilizarse la Marca B con una temperatura del horno de 350ºC y un tiempo de horneado de 38 minutos para minimizar la pérdida de humedad. Usando esos valores para las entradas, puede esperarse que la pérdida de humedad sea de aproximadamente 3,3034, que es bastante baja en comparación con la pérdida de humedad de los pasteles recolectados como parte del experimento.

¡Éxito! Ahora pueden utilizarse estos ajustes óptimos y nunca más se perderá el tiempo horneando un pastel seco.