- Detalles
- Categoría: Comsol
- Visto: 3791
Suponemos que más de uno con algo de curiosidad se habrá preguntado por qué las bolas de golf son como son.
Para estos curiosos o para los aficionados al golf, varias entradas en el blog de COMSOL nos explican algunos detalles de este deporte. Por ejemplo un par de artículos explican la evolución de las bolas de golf y el impacto del palo en la bola y la física inherente a los hoyuelos de los últimos modelos. También, en otro artículo se explica la mecánica del swing de golf.
Esperamos que estos artículos le permitan saber algo más de este deporte. Si encima es aficionado y mejoran su juego, ya será de premio. Pero nos tememos que igualmente requerirá muchas horas de entreno y algún buen profesional que le explique la técnica de forma práctica.
- Detalles
- Categoría: Noticias
- Visto: 4458
Aquellos interesados en cursar el Máster Universitario Online en Simulación Numérica en Ciencia e Ingeniería con COMSOL Multiphysics (MUCOM) que, por algún motivo, no hayan podido realizar la preinscripción y matriculación antes del 25 de septiembre podrán solicitar una excepción a la Dirección Académica. La Dirección Académica evaluará su solicitud y, en caso de ser aprobada, el interesado podrá incorporarse a los estudios del máster.
El alumno que se matricule en este periodo tendrá a su disposición todas las clases impartidas hasta el momento, pues son grabadas, y todo el material docente que se encuentra publicado en las correspondientes páginas del Campus Virtual. Además, tanto la Dirección Académica como los diferentes profesores que hayan iniciado su enseñanza en el máster, facilitarán la recuperación y puesta al día de toda la docencia impartida hasta el momento, mediante tutorías personales en línea con el propio alumno.
- Detalles
- Categoría: NAG
- Visto: 3728
La última Mark de la librería NAG® ya está disponible para su descarga. Mark 27.3 presenta un resolvedor simbólico de Matriz de Correlación más Cercana (NCM), FEAST Eigensolver y más resolvedores de diferenciación automática (AD) de segundo orden.
Destacamos el nuevo solucionador NCM para calcular el adjunto simbólico de la matriz de correlación más cercana (NCM). Calcular derivadas del NCM permite encontrar sensibilidades a los datos de entrada. El adjunto simbólico calcula la derivada matemáticamente, lo que da como resultado una rutina que es 70 veces más rápida y utiliza 2500 veces menos memoria que el adjunto algorítmico. Se accede al adjunto simbólico a través de un nuevo modo para el solucionador g02aa. Anteriormente, esto se podía hacer en la Librería NAG AD calculando el adjunto algorítmico, que diferenciaba el código línea a línea.
- Detalles
- Categoría: Maple
- Visto: 4420
Tuvimos la gran oportunidad de entrevistar al Dr. Trefor Bazett, un profesor de matemáticas de la Universidad de Victoria, que también publica regularmente videos en su canal de YouTube que explican una amplia variedad de conceptos matemáticos, desde hechos matemáticos interesantes hasta cursos universitarios completos. También le puede reconocer por el reciente webinar que realizó sobre el aprendizaje interactivo efectivo. Si es Vd. profesor, y especialmente si está tratando de encontrar formas de mantener a sus estudiantes interesados en la enseñanza de matemáticas en línea, siga leyendo para conocer algunos buenos consejos y la perspectiva de alguien que ya ha creado una gran cantidad de seguidores en línea. Si no es profesor, ¡siga leyendo de todos modos! Puede que no todos seamos profesores, pero todos hemos sido (¡o lo somos!) estudiantes. ¡Y como estudiantes, probablemente todos tengamos algunas opiniones sobre cómo se deben enseñar las cosas! Siga leyendo para obtener una nueva perspectiva, y tal vez incluso algunas nuevas formas de abordar su aprendizaje en el futuro.
¿Cuáles son algunos de los desafíos únicos que presenta la enseñanza de matemáticas en línea y cómo los supera?
Enseñando en línea trabajo mucho más duro para mantener realmente la atracción de los estudiantes. Creo fervientmente en el aprendizaje activo, lo que significa que los estudiantes participan activamente en su aprendizaje resolviendo problemas, haciendo preguntas y estableciendo conexiones ellos mismos. ¡Esto puede parecer un poco extraño viniendo de un YouTuber, ya que ver un video es una de las formas más pasivas de aprender! Cuando se trata de una clase presencial, las presiones sociales de ese entorno facilitan la creación de un entorno de aprendizaje de apoyo que fomenta la participación activa. Cuando enseño en línea, trato de organizar actividades interactivas y oportunidades de aprendizaje en torno a mis videos, ¡pero al menos para mí es un desafío! Me resulta más fácil de muchas maneras pensar en los componentes pasivos de mi enseñanza, como crear un video que presenta un tema, pero diseñar actividades de aprendizaje en torno a esos videos en los que los estudiantes están comprometidos y se sienten parte de una comunidad de apoyo es crucial.
¿Cree que la experiencia de enseñar en línea ha dado lugar a tendencias positivas en la educación que perdurarán una vez que los estudiantes regresen al aula?
Absolutamente. Queramos o no, los profesores ahora tienen experiencia y habilidades para integrar la tecnología en su aprendizaje porque muchos de nosotros tuvimos que descubrir cómo enseñar en línea. La gran pregunta es ¿cómo aprovechamos estas nuevas herramientas, experiencias y recursos tecnológicos que hemos creado para cuando regresemos al aula física? ¿Podemos reincorporar de una nueva manera, por ejemplo, los videos que creamos para la pandemia? Tenemos tantas herramientas tecnológicas increíbles y, por supuesto, debo mencionar a Maple Learn como una de ellas. - que hizo posible que los estudiantes participaran en el aprendizaje interactivo en el espacio en línea, pero ahora podemos pensar en todas las formas de aprovechar estas herramientas en el aprendizaje cara a cara, ya sea como parte de una demostración en el aula, actividades de los estudiantes en el aula, o actividades fuera de clase.
¿Cómo cree que ha cambiado la afluencia de educadores matemáticos como usted en las redes sociales y cómo cambiará la forma de la educación matemática?
Estoy muy orgulloso de la comunidad de educación matemática en YouTube y otras plataformas, la calidad y diversidad de la educación matemática en línea es realmente increíble. Tener acceso universal a materiales educativos gratuitos de alta calidad realmente puede ayudar a nivelar el campo de juego. Pero el aula también desempeña un papel fundamental, ya sea en persona o en línea. Ver videos de YouTube en un canal de matemáticas no será suficiente para la mayoría de las personas. Debe practicar activamente las matemáticas en un entorno de apoyo, recibir comentarios sobre su progreso y obtener ayuda cuando la necesite. Siento que hay muchas oportunidades para que los maestros aprovechen los materiales en línea, por ejemplo, vinculando a los estudiantes con un excelente contenido expositivo mientras los maestros en clase se enfocan en diseñar actividades de aprendizaje activo y atractivas.
¿Qué le hizo decidirse a crear un canal de YouTube? ¿Tiene algún consejo para otros que quieran hacer lo mismo?
Mi primer curso en línea se diseñó de forma asincróna, por lo que necesitaba un lugar para alojar los videos de ese curso. ¿Por qué no YouTube? Solo tenía veinte estudiantes en el curso, y nunca imaginé que nadie más los vería, ¡y mucho menos millones de ellos! Pero cuando noté que mi primer video de matemáticas fue recogido por el algoritmo de búsqueda de YouTube y seguí recibiendo comentario tras comentario agradeciéndome, me di cuenta de que realmente había una gran necesidad de contenido de educación matemática de calidad en YouTube.
¡Mi mayor consejo es solo comenzar! Tu primer video no será (¡probablemente!) el que será recogido por el algoritmo de YouTube, pero es el que te inicia en ese camino y desarrolla tus habilidades para contar historias matemáticas, hablar a la cámara, utilizando la tecnología, etc. No se preocupe si ese primer video es completamente perfecto o imita el "estilo" de otros YouTubers, utilícelo como una oportunidad para construir. Si quiere saber más sobre mi proceso para hacer videos, comparto mucho de mi proceso aquí.
¿Cuál cree que es la mejor manera para que los estudiantes aborden los problemas de las tareas?
La tarea a menudo se percibe, de manera bastante comprensible, como una tarea pesada que frustrantemente se tiene que hacer. Si esa es la percepción, entonces también es comprensible que los estudiantes adopten comportamientos que podrían ayudarlos a obtener puntos en la tarea, pero que no son muy efectivos para el aprendizaje. Sin embargo, si piensa en la tarea como una oportunidad para aprender y una oportunidad para obtener retroalimentación sobre cuán efectivo es su aprendizaje, ahora puede involucrarse en comportamientos mucho más efectivos.
Mi sugerencia es que primero se intente siempre el problema de verdad por uno mismo. Si estoy completamente atascado, realmente me gusta escribir todo lo que sé sobre el problema, como las definiciones de las palabras matemáticas involucradas en el problema. Esto hace que sea mucho más fácil ver todas las piezas y descubrir cómo ensamblarlas como un rompecabezas.
Creo firmemente en el aprendizaje autorregulado, en el que identifica con precisión lo que se sabe y lo que no, y luego adapta su aprendizaje para concentrarse en las partes que son más desafiantes. Las herramientas tecnológicas como Maple Learn, que brindan soluciones paso a paso a muchos tipos de manipulaciones matemáticas, pueden ayudar con esta autorregulación, por ejemplo, verificando que hiciste correctamente algún álgebra engorrosa o precisamente dónde está el error.
Incluso si ha resuelto el problema, ¡aún puede aprender más de él! Puede imaginarse cómo el instructor podría modificar esa pregunta en una prueba y, de ser así, ¿cómo respondería? Puede trazar cómo este problema se conecta con otros problemas. Puede escribir un mapa conceptual de la imagen más grande y dónde encaja este problema. Tengo un video completo con muchas más estrategias para abordar los problemas de la tarea más allá de obtener la respuesta.
Como profesor, ¿cuál es su opinión sobre proporcionar a los estudiantes soluciones paso a paso?
Las soluciones paso a paso definitivamente tienen un papel. Para dominar las matemáticas, necesita dominar muchos pequeños detalles, y luego pueden comenzar a formarse las conexiones más profundas entre las ideas. Las soluciones paso a paso realmente pueden ayudar a los estudiantes a dominar todos esos pequeños detalles porque pueden identificar la ubicación precisa de su confusión en lugar de simplemente notar que obtuvieron la respuesta incorrecta y no pueden identificar dónde está exactamente su confusión. Creo que también pueden ayudar a reducir la ansiedad matemática, ya que los estudiantes pueden estar seguros de que tendrán las herramientas para comprender el problema.
Sin embargo, es importante utilizar las soluciones paso a paso de manera apropiada para que los estudiantes las utilicen como una herramienta de aprendizaje de apoyo y no como una muleta. A veces, los estudiantes intentan aprender matemáticas imitando los pasos de algún proceso sin comprender profundamente por qué o cuándo aplicar los pasos. Puede haber una gran brecha entre seguir una solución de otra persona y poder llegar a ella usted mismo. Aquí es donde los profesores tienen un papel importante que desempeñar. Necesitamos ser claros en nuestros mensajes a los estudiantes sobre cómo usar estos apoyos de manera efectiva, así como hacer preguntas formativas de manera constante que animen a los estudiantes a reflexionar sobre las matemáticas que están haciendo y brinden oportunidades para que los estudiantes resuelvan problemas de manera creativa.
En su seminario web habló un poco sobre el modelo de "aula invertida". ¿Tiene algún consejo para los educadores que quieran avanzar más hacia un aula invertida donde el tiempo en clase se centre en la discusión y la exploración?
Realmente me encantan los enfoques de aula invertida. La gran idea aquí es que los estudiantes establezcan un conocimiento básico del contenido antes de la clase, por ejemplo, al ver mis videos previos a la clase, para que estén capacitados para realizar un aprendizaje activo más colaborativo en clase. Por tanto, los apoyos sociales de la clase se centran en los objetivos de aprendizaje de nivel superior. Sin embargo, por mucho que me encanta este enfoque, es solo una de las opciones que comienzan a cambiar hacia el aprendizaje centrado en el estudiante. Mi consejo principal es comenzar poco a poco, tal vez simplemente agregando un problema colaborativo de cinco minutos a cada clase antes de pasar a una pedagogía de aula invertida. En lo que a mí respecta, pasaron algunos años en los que seguí agregando más y más elementos de aprendizaje activo a mi salón de clases y cada vez que lo hice sentí que funcionaba tan bien que agregué un poco más.
¿Cuáles son algunas de las formas en que los maestros pueden permitir que los estudiantes tomen el control de su aprendizaje?
¡Esto es tan importante! A veces, la enseñanza puede ser demasiado paternalista, pero creo que deberíamos confiar más en nuestros estudiantes. ¡Dé a los estudiantes el tiempo y el espacio para intentar abordar problemas interesantes y sucederá! Nuestro papel como maestros es crear un entorno de aprendizaje de apoyo que propicie el aprendizaje de los estudiantes. Algunos ingredientes que creo que pueden ayudar son, en primer lugar, animar a los estudiantes a colaborar y apoyarse entre sí. Las matemáticas son una disciplina inherentemente colaborativa en la práctica, pero esto también puede ser muy útil para el aprendizaje. En segundo lugar, podemos proporcionar un andamiaje eficaz en los problemas que brindan a los estudiantes vías para que los estudiantes comiencen y progresen. En tercer lugar, las herramientas tecnológicas como Maple Learn nos permiten eliminar parte de la fricción de cosas como gráficas, álgebra engorrosa, y otros cálculos precedurales, lo que significa que en su lugar podemos enfocar nuestro aprendizaje en desarrollar una comprensión conceptual.
En su opinión, ¿cómo podemos motivar a los estudiantes a aprender matemáticas?
Autenticidad. La motivación a veces se divide entre motivaciones intrínsecas (disfrute de la asignatura en sí) y motivaciones extrínsecas (por ejemplo, querer sacar una buena nota) y, en general, aprendemos de forma más eficaz y profunda cuando estamos intrínsecamente motivados. Para capturar la motivación intrínseca, siempre trato de hacer que mi enseñanza y los problemas en los que pido a los estudiantes que trabajen se sientan auténticos. Eso podría significar que el problema se conecta con desafíos del mundo real donde los estudiantes pueden ver cómo las matemáticas se relacionan con el mundo, ¡pero no tiene por qué ser así! Un problema que se mantiene en pura matemática pero pregunta y responde problemas matemáticos interesantes y deleita al alumno también es excelente para la motivación intrínseca. Si los estudiantes están capacitados para abordar problemas auténticos en un entorno de aprendizaje de apoyo, esa motivación vendrá naturalmente.
¿Cuál es su número, expresión matemática o factor matemático favorito?
En algún lugar de la superficie de la tierra, hay un lugar que tiene exactamente la misma temperatura y presión que el lugar exactamente opuesto al otro lado de la tierra. ¡Esto es cierto sin importar los posibles patrones climáticos que tenga en toda la tierra! Que esto tiene que ser siempre cierto se debe al teorema de Borsuk-Ulam y si quieres saber más sobre este teorema y sus muchas consecuencias, he hecho un video completo al respecto.
¿Algún pensamiento de despedida?
Al comienzo de cada nuevo año escolar, leo sobre docenas de ideas interesantes y me siento tentado a pensar "¡Quiero probar eso!". Sugiero en lugar de encontrar una cosa a mejorar en el año anterior, una cosa en la que realmente se pueda invertir y que marcará la diferencia para sus estudiantes. ¡No es necesario reinventar la rueda todos los años!
- Detalles
- Categoría: Comsol
- Visto: 4291
En COMSOL News 2021, los ingenieros y científicos comparten cómo están utilizando COMSOL® para desarrollar productos basados en la simulación, la democratización de la simulación, optimización del diseño, y mucho más. Vea cómo un proyecto de ingeniería ecológica está literalmente añadiendo vegetación al paisaje urbano y cómo las turbinas de agua de las mareas están generando energía limpia al tiempo que protegen la vida marina. Lea sobre la investigación actual y los logros académicos que involucran la capacidad de camuflaje acústico de las alas de una polilla, el procesado de materiales de alto rendimiento y la enseñanza de conceptos de ingeniería química utilizando laboratorios virtuales y una app galardonada con un premio.
Los temas incluyen:
- Altavoces de entretenimiento para el hogar
- Cables de alta tensión submarinos
- Marcapasos cardíacos sin cables
- Educación en ingeniería usando aplicaciones de simulación
- Desarrollo de productos de automoción
- Cajas de altavoces
- Intercambiadores de calor industriales
- Turbinas de energía mareomotriz
- Dispositivos de medición de flujo de gas
- Un sistema urbano de gestión de aguas pluviales.
- Camuflaje vibroacústico
- Deposición de vapor químico
- Digitalización de test, inspección y certificación
Haga clic en el enlace inferior para leer la versión digital.
- Detalles
- Categoría: Minitab
- Visto: 7983
Por Joshua Zable.
En términos generales, si es ingeniero químico, probablemente estará desarrollando y diseñando procesos de fabricación de productos químicos. A diferencia de otros ingenieros, eso significa que es posible que deba aplicar los principios de la química, la biología, la física y las matemáticas para resolver problemas que involucran la producción o el uso de productos químicos, combustibles, medicamentos, alimentos y muchos otros productos. Con todo ese tiempo dedicado a las ciencias, si no ha dedicado tanto tiempo a la estadística como desearía, no se preocupe, ¡Minitab está aquí! Ahora, hablemos de por qué el análisis de varianza (ANOVA) puede ser el arma secreta de un ingeniero químico.
POR QUÉ DEBERÍA CONOCER ANOVA
Muchas aplicaciones industriales involucran experimentos donde el objetivo es comprender si los grupos son diferentes. En términos estadísticos, consideramos un factor, digamos el tipo de catalizador, y queremos entender si los niveles de ese factor, digamos catalizador 1, catalizador 2, catalizador 3 y catalizador 4, son significativamente diferentes estadísticamente entre sí. Cuando las mediciones en los grupos son continuas y se cumplen otras suposiciones, utilizamos ANOVA para comparar las medias de los grupos. En cierto sentido, el nombre "Análisis de varianza" es inapropiado, porque estamos interesados en comparar las medias de los grupos. Sin embargo, al analizar la variación en los datos dentro de los niveles de grupo y entre los grupos, podemos determinar si las medias del grupo son estadísticamente diferentes.
ANOVA prueba la hipótesis nula de que las medias de la población (señaladas con el símbolo µ) son todas iguales. Estimaremos las medias poblacionales utilizando las medias muestrales. Si se rechaza esta hipótesis nula, concluimos que las medias de la población no son todas iguales.
La hipótesis nula:
Ho: µCatalizador 1 = µCatalizador 2 = µCatalizador 3 = µCatalizador 4
.png)
En lenguaje sencillo, asumimos que las medias son todas iguales en todos los grupos, y recopilamos evidencia en contra de eso, lo que significa que si observamos grandes diferencias de medias entre estas medias, estaremos más seguros al rechazar esa creencia y al asumamir que hay diferencias dentro de los niveles de grupo.
EJEMPLO DE ANOVA DE UN FACTOR
Imagine que una ingeniera química quiere comparar el rendimiento del producto utilizando cuatro catalizadores diferentes. Ella calentará el catalizador con el producto para obtener una reacción. Utilizando ANOVA, la ingeniera puede determinar si el rendimiento del producto usando diferentes catalizadores difiere significativamente.
Primero, la ingeniera recopila sus datos, como se puede ver a continuación.
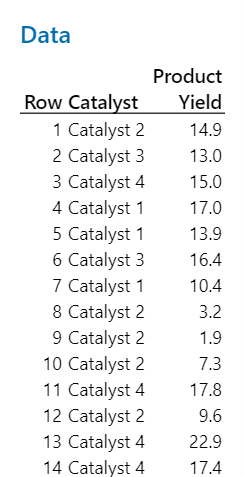
A continuación, la ingeniera corre un ANOVA de un solo factor.
El p-valor para el ANOVA de rendimiento del producto es pequeño, lo que indica que existe una probabilidad muy pequeña de que hubiéramos observado estos resultados si la hipótesis nula es cierta, es decir, que las medias del catalizador son todas iguales. Debido a que el valor p es menor que un nivel de significancia del 5% (estamos usando un alfa = 0.05), rechazamos la hipótesis nula. Concluimos que t, el rendimiento medio del producto, difiere entre los grupos catalizadores.

La ingeniera sabe que algunas de las medias del grupo son diferentes. La siguiente pregunta lógica es, ¿cuáles?
USO DEL MÉTODO DE TUKEY PARA REALIZAR LAS COMPARACIONES MÚLTIPLES
Si bien ANOVA nos enseñó que algunas de las medias del grupo son diferentes, la ingeniera necesita una comparación más profunda para comprender qué medias de grupo son diferentes. Minitab proporciona "Comparaciones" por esta misma razón. En nuestro ejemplo, la ingeniera química usa las comparaciones de Tukey para probar formalmente las diferencias entre los pares de grupos, para comprender cuáles son estadísticamente significativamente diferentes.
La prueba de comparación múltiple de Tukey es la prueba más conservadora de varias pruebas que se pueden utilizar para determinar qué medias entre un conjunto de medias difieren del resto. El método de Tukey se usa después de ANOVA (por lo que es posible que escuche que se hace referencia al método como una prueba post hoc) y se puede utilizar para crear intervalos de confianza para todas las diferencias por pares entre las medias de los niveles de factor mientras se controla la tasa de error familiar a un nivel que usted especifique.
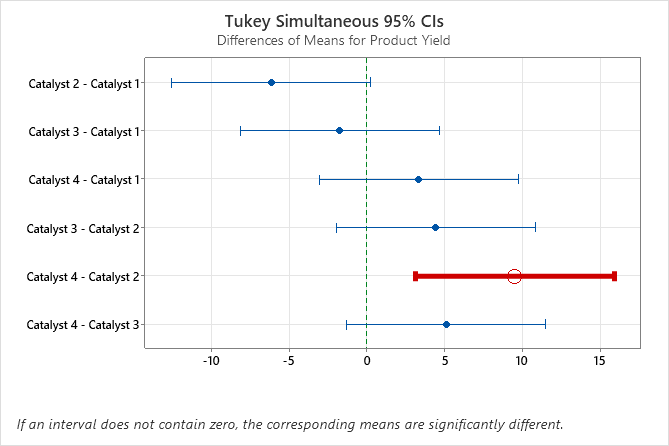
En nuestro ejemplo, el gráfico que incluye los intervalos de confianza simultáneos de Tukey muestra que el intervalo de confianza para la diferencia entre las medias de los Catalizadores 2 y 4 es de 3,114 a 15,886. Este rango no incluye cero, lo que indica que la diferencia entre estas medias es significativa. La ingeniera puede usar esta estimación de la diferencia para determinar si la diferencia es prácticamente significativa.
Por el contrario, los intervalos de confianza para los pares de medias restantes incluyen todos cero, lo que indica que las diferencias no son significativas.
¿POR QUÉ NO CORRER UN MONTÓN DE PRUEBAS T PARA IDENTIFICAR DIFERENCIAS?
Es una gran pregunta, ¡y surge mucho! La respuesta tiene que ver con el riesgo de cometer un error, específicamente, el riesgo de concluir incorrectamente que existe una diferencia estadísticamente significativa, que es lo que llamamos nuestro riesgo alfa. Cuando realizamos una prueba, hay un 5% de probabilidad de que digamos que hay una diferencia, cuando en realidad no la hay. Para los 4 catalizadores, ¡eso daría como resultado 6 pruebas t!
¿Cuál es la probabilidad de observar al menos un resultado significativo debido al azar?
P(al menos un resultado significativo) = 1 - P (sin resultados significativos)
= 1 - (1 - 0.05)6
≈ 0,264
Entonces, con 6 pruebas consideradas, tenemos un 26% de posibilidades de observar al menos un resultado significativo, incluso si todas las pruebas no son realmente significativas. Las pruebas post hoc controlan la tasa de error de los experimentos; para decirlo de manera más simple, queremos asegurarnos de que la probabilidad de que declaremos incorrectamente que cualquier par de catalizadores es diferente permanezca en el 5%. ¡Eso es exactamente lo que hace la prueba de Tukey por nosotros!
LAS RESPUESTAS ESTÁN EN ANOVA
El uso de ANOVA permite a un ingeniero químico probar mezclas para ver si los resultados son estadísticamente significativos. Igualmente importante, también puede determinar si todo el grupo es diferente o quizás solo un subsegmento del grupo utilizando pruebas de comparación. En nuestro ejemplo, solo el catalizador 2 y el catalizador 4 tienen diferencias estadísticamente significativas con respecto al rendimiento del producto. Con base en esta información, la ingeniera química puede comenzar a mirar los otros catalizadores para determinar qué catalizador es el más rentable, tiene la vida útil más larga o es más fácil de acceder sabiendo que producirá una cantidad similar de producto.
- Detalles
- Categoría: Maple
- Visto: 34159
Maple Flow y Mathcad® tienen sus propios principios de diseño. En el caso de Maple Flow, estos principios se asientan sobre los de Maple. Maple Flow hace uso de una interfaz flexible tipo pizarra para recubrir un amplio conjunto de resolvedores numéricos y simbólicos, impactantes formas de visualizar datos y funciones, conectividad con MATLAB® y fuentes de datos en red y en la nube y un modelo de licencias tradicional.
Licencia
| Mathcad Prime | Maple Flow | |
| Modelo de licenciamiento | Suscripción | Perpetuo |
| Con una licencia perpetua, su trabajo seguirá siendo suyo por tiempo indefinido. No quedará bloqueado si decide no continuar con una suscripción o si el producto se discontinua. | ||
| Actualizaciones para un solo usuario | No. Los usuarios deben estar en mantenimiento activo para obtener actualizaciones o comprar nuevas licencias. | Sí. Los usuarios pueden comprar actualizaciones con descuento. |
| Presupueste las actualizaciones cuando más le convenga a Vd., no al proveedor de software. | ||
| Licencias con descuento para usuarios sin aplicación comercial o afiliación académica | No. | Sí. |
Matemáticas
| Mathcad Prime | Maple Flow | |
| Matemáticas numéricas | Limitado. | Amplia gama de funciones en toda las áreas de matemáticas, ciencias, ingeniería y tecnología. |
| Las matemáticas numéricas de alto rendimiento implican que puede resolver más problemas sin comprar extensiones de herramientas. Una gestión de memoria superior significa que puede analizar sistemas más grandes con los mismos recursos informáticos. | ||
| Matemáticas simbólicas | Muy limitado con numerosas lagunas. | Extenso, el mejor de su clase. |
| Elimine el riesgo de la manipulación algebraica de ecuaciones y resuelva un rango mucho más amplio de ecuaciones. | ||
| Lenguaje de programación | Limitado, útil solo para programas pequeños. | Con todas las funciones, con conversión de código a otros lenguajes. |
Visualización
| Mathcad Prime | Maple Flow | |
| Visualización y trazado | Número limitado de gráficos, poco flexibles. | Espectro completo de gráficos y visualizaciones flexibles y de alto impacto. Altamente personalizables. |
| Atraiga a su audiencia y cree gráficos con calidad de publicación. | ||
Conectividad
| Mathcad Prime | Maple Flow | |
| MATLAB ® | No. | Sí. |
| Maximice la inversión que ha realizado en MATLAB con conectividad bidireccional completa. Desarrolle modelos simbólicos en Maple Flow y luego genere código para MATLAB. | ||
| Fuentes de datos de Internet y de la red | No. | Sí. |
| Acceda a los datos desde cualquier lugar, no solo desde su sistema de archivos local. | ||
Mathcad es una marca comercial registrada de PTC Inc. o sus subsidiarias en EE. UU. Y en otros países. MATLAB es una marca registrada de The MathWorks, Inc.