- Detalles
- Categoría: Comsol
- Visto: 6338
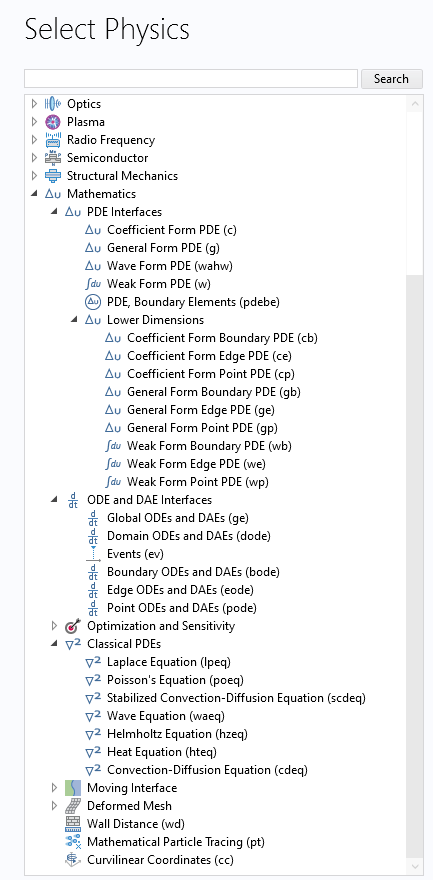
En COMSOL Multiphysics, la rama de Matemáticas contiene interfaces para resolver Ecuaciones en Derivadas Parciales (EDP), Ecuaciones Diferenciales Ordinarias (ODE) y Ecuaciones Diferenciales Algebraicas (DAE), realizar análisis de sensibilidad, modelar mallas móviles y geometrías deformadas, entre otras cosas. Dicha rama se encuentra en el Mathematics Module, que viene por defecto con la adquisición de la Licencia de COMSOL Multiphysics. Las diferentes interfaces son:
- PDE Interfaces: Resuelve EDP en forma de coeficiente, forma general y forma débil.
- ODE and DAE Interfaces: Permite añadir ecuaciones globales, ecuaciones independientes de la posición que representan otros estados.
- Optimization and Sensitivity: Permite la optimización (requiere Optimization module) y análisis de sensibilidad (por defecto en licencia básica).
- Classical PDE: Permite trabajar con casos especiales de EDP en forma de coeficientes. Dichas son la Ecuación de Laplace, Poisson, Ondas, Calor, Helmholtz, Convección-Difusión y Convección- Difusión Estabilizada.
- Deformed Mesh: Permite añadir estudios considerado una geometría deformada y de malla deformada como resultado de una carga.
- Wall Distance: Permite resolver la Ecuación de la eikonal para obtener la distancia a las paredes, lo cual se emplea en modelización de la turbulencia en fluido dinámica.
- Curvilinear Coordinates: Permite incorporar un sistema de coordenadas curvilíneo para definir propiedades de materiales del tipo anisotrópico, siguiendo la geometría de un objeto.
En esta ocasión nos centraremos en las EDP para dar una interpretación útil a los usuarios sobre cada término en la ecuación.
Las EDP y su interpretación
La EDP con una única variable dependiente u, en forma general en dominio Ω y sus condiciones de contorno en la frontera ∂Ω, se encuentran de la siguiente manera en la General Form PDE de COMSOL Multiphysics:
Los términos Γ, f, g, q, R y r son definidos por el usuario. Es decir, pueden ser funciones de las coordenadas espaciales, la solución u y las derivadas espaciales de u, así como otras variables definidas por el usuario. Los términos f, g, q, R y r son escalares. El término Γ es el vector de flujo.
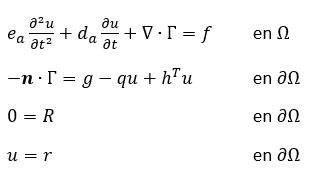
El vector Γ puede representar el flujo de una cantidad conservada, como calor, carga, masa o momento. Este flujo está usualmente relacionado mediante una ley material con el gradiente de la variable dependiente. Por lo tanto, Γ puede ser un vector cuyas componentes son funciones de las derivadas de la variable dependiente. El vector de flujo Γ puede también contener términos que son proporcionales a un campo de velocidad, cuando se tiene un transporte convectivo.
Las condiciones de contorno de la segunda línea de la ecuación corresponden a una condición de contorno tipo Neumann. Esta condición se denomina de flujo o fuente, debido a que especifica el valor del flujo numérico Γ en el contorno.
En la tercera y cuarta línea se tienen condiciones contorno del tipo Dirichlet. En el campo e los Elementos Finitos se les llama esenciales porque imponen una restricción en el espacio de prueba, que no es parte de la ecuación principal. La restricción de la tercera línea indica que una expresión arbitraria R es igual a cero en el contorno. La condición de Dirichlet de la línea 4 es un caso particular, especificando el valor de la variable dependiente en el contorno.
Forma de coeficientes
La forma de coeficientes de la EDP se encuentra de la siguiente manera en la Coefficient Form PDE interface de COMSOL Multiphysics. La primera línea de la ecuación es la EDP, que se cumple en el en el dominio Ω. Las ecuaciones en la segunda y tercera línea son las condiciones de contorno, que deben cumplir en ∂Ω. La segunda ecuación es una generalización de la condición de contorno de Neumann. La tercera ecuación es una restricción general, con la condición de contorno de Dirichlet como caso especial.
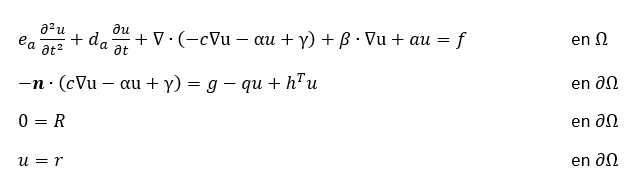
El usuario puede definir los coeficientes c, α, γ, β y a y los términos de contorno f, g, R y r. Cada uno de ellos pueden ser funciones de las coordenadas espaciales, así como variables dependientes y otras predeterminadas o variables definidas por el usuario y parámetros. Notar que para una única variable dependiente u, todos los coeficientes en la ecuación anterior son escalares excepto α, β y γ, que son vectores con 𝑛 componentes. El coeficiente c puede ser especificado como un escalar o como una matriz para materiales anisotrópicos.
Dualidad entre General Form y Coefficient Form PDE
La forma general y de coeficientes guardan una estrecha relación. En efecto, la forma de coeficientes es un caso particular de la forma general. Si se aplica una sustitución (ver ecuaciones siguientes) en la forma general, ésta se convierte en la forma de coeficientes. Este hecho da al usuario la posibilidad de escoger la representación en la que sea más sencillo trabajar una EDP.
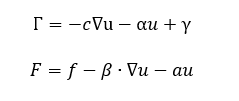
Una interpretación de los coeficientes de EDP

Ejemplos
Existen numerosos ejemplos de modelado basado en las interfaces del Mathematics Module. Por mencionar algunos que se encuentran disponible en el material de COMSOL tenemos: kdv equation-and solitons [1], Electrical Signals in a Heart [2] y A Lorenz Attractor [3]. Una breve descripción de cada modelo viene a continuación.
La Ecuación de Korteweg-de Vries (KdV) se creó en 1895 para modelar ondas de agua. Dado que la ecuación no introduce la disipación, las ondas viajan aparentemente para siempre. Estas ondas ahora se llaman solitones, que pueden viajar largas distancias sin alterar su forma o velocidad. Hoy, la ecuación KdV se usa para comprender las ondas de luz. Como resultado, una de las principales aplicaciones modernas de los solitones es en fibras ópticas (Figura 1).
Figura 1: Resultado donde los solitones mantienen la forma intacta al colisionar, reapareciendo.
Modelar la actividad eléctrica en el tejido cardíaco es un paso importante para comprender los patrones de contracciones y dilataciones en el corazón. El corazón produce pulsos eléctricos rítmicos, que desencadenan las contracciones mecánicas del músculo. Varias afecciones cardíacas implican un riesgo elevado de reingreso de las señales. Esto significa que se altera el pulso constante normal, una condición grave y aguda que a menudo se denomina arritmia. La profesora Dra. Simonetta Filippi y el Dr. Christian Cherubini del Campus Universitario Biomédico di Roma, Italia, han proporcionado este modelo. En sí, son dos modelos matemáticos que describen diferentes aspectos de la propagación de la señal eléctrica en el tejido cardíaco: las ecuaciones de FitzHugh-Nagumo y las ecuaciones de Ginzburg-Landau, ambas resueltas en la misma geometría (Figura 2).

Figura 2: Solución de las ecuaciones de FitzHugh-Nagumo a 120 s.
Un atractor de Lorenz se puede describir mediante un sistema de ecuaciones diferenciales ordinarias (El sistema Lorenz). A principios de la década de 1960, Lorenz descubrió el comportamiento caótico de este sistema para ciertos valores de parámetros y condiciones iniciales. La solución, cuando se grafica como un espacio de fase, se asemeja a la Figura 3. Este ejemplo utiliza el método explícito de Dormand-Prince para resolver las ODE y un diagrama de trayectorias de puntos para visualizar el atractor de Lorenz.

Figura 3: Forma del Atractor de Lorenz.
Estos 3 modelos se encuentran en la Librería de Aplicaciones de COMSOL y además están descritos en el Blog de COMSOL Multiphysics [4].
Referencias
[1] https://www.comsol.com/model/the-kdv-equation-and-solitons-85
[2] https://www.comsol.com/model/electrical-signals-in-a-heart-981#:~:text=Modeling%20the%20electrical%20activity%20in,mechanical%20contractions%20of%20the%20muscle
[3] https://www.comsol.com/model/lorenz-attractor-16635
[4] https://www.comsol.com/blogs/3-examples-of-equation-based-modeling-in-comsol-multiphysics/
- Detalles
- Categoría: Lakes
- Visto: 4592
El preprocesador de datos meteorológicos de AERMET contiene muchas funcionalidades diferentes diseñada para ayudar a los usuarios a realizar tareas de control de calidad a medida que los datos son procesados. Estas incluyen la capacidad de auditar variables específicas, modificar rangos de datos válidos, y más.
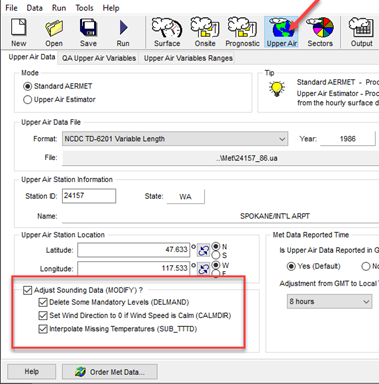
Una funcionalidad construida en Upper Air Pathway de AERMET está diseñada para comprobar problemas potenciales en el sondeo y potencialmente poder corregir esos problemas. Esta funcionalidad es la palabra clave MODIFY, y consta de tres acciones:
- DELMAND: Se eliminan los niveles obligatorios dentro del uno por ciento de un nivel de significación (respecto a la presión).
- CALMDIR: Las direcciones de viento no nulo se ponen a cero si la velocidad de viento es calma (0).
- SUB_TTDD: Las temperaturas de bulbo seco o de punto de rocío que faltan se reemplazan por valores interpolados utilizando datos de los niveles inmediatamente por encima y por debajo del nivel que falta.
Antes del lanzamiento del lmodelo 22112, al usar la opción MODIFY se aplicaban las tres acciones. AERMET 22112 brinda a los usuarios un mayor control sobre estas acciones al permitir que los modeladores elijan qué acciones aplicar.
En AERMET View versión 11, las opciones MODIFY se encuentran en Upper Air Pathway. Seleccione el botón Upper Air y marque la casilla de verificación Adjust Sounding Data (MODIFY) para utilizar la palabra clave. Cuando el ejecutable de AERMET seleccionado es la versión 22112, los usuarios pueden habilitar (marcar) o deshabilitar (desmarcar) cada acción individualmente.
- Detalles
- Categoría: Minitab
- Visto: 5063
Por Jon Finerty
El plazo de entrega es un parámetro crucial de gestión de la cadena de suministro. Es fundamental que las empresas entiendan cuánto tarda un producto en pasar por el canal desde el pedido original hasta la entrega, ya sea que estén comprando, vendiendo o moviendo bienes y materiales internamente.
Con los consumidores cada vez más acostumbrados a recibir sus pedidos al día siguiente, o incluso el mismo día, las cadenas de suministro se han centrado cada vez más en la parte de entrega de sus procesos. Es decir, cadenas de suministro que quieren seguir siendo exitosas.
Podemos definir una entrega exitosa como brindar a los clientes lo que necesitan, en la cantidad correcta, en el momento correcto, y hacerlo de manera consistente. La entrega ahora se considera el requisito más fundamental de cualquier negocio de fabricación o distribución. Usando el poder del análisis de datos, Minitab puede ayudar a las empresas a optimizar la entrega, optimizar su cadena de suministro y aumentar la satisfacción del cliente.
Medir la velocidad de entrega
El tiempo que se tarda en entregar un producto final al cliente final es una medida clave para los profesionales de la cadena de suministro. Usando un conjunto de datos de muestra y algunas estadísticas descriptivas simples, el siguiente ejemplo muestra que el promedio (o la media) del tiempo de entrega es de entre 54 y 55 horas. Los datos también indican que el tiempo mínimo es de 40 horas y el tiempo máximo es de 75 horas, por lo que proporciona un rango de los tiempos más rápidos y más lentos que ayudan a establecer objetivos.

Establezca una meta y haga una lluvia de ideas sobre los posibles factores que afectan a la entrega
Una entrega retrasada puede costarle a la empresa no solo en términos de la experiencia del cliente, sino que también puede afectar directamente a las ventas. Si una compañía no puede cumplir su promesa de una entrega oportuna, es mucho menos probable que sus clientes vuelvan a comprar en el futuro. Establezca un objetivo comercial estratégico para entregar bienes dentro de un período de tiempo determinado. En este ejemplo, establezcamos un objetivo realista de 50, lo que representa una mejora de ~10% en el tiempo de entrega.
A continuación, haga una lluvia de ideas sobre las posibles variables que podrían estar afectando el plazo de los bienes entregados. Esto podría ser cualquier cosa, desde el tamaño del paquete, la antigüedad del vehículo, las condiciones climáticas o incluso el conductor que realiza la entrega. El siguiente diagrama muestra un ejemplo de un árbol CT, una de las muchas herramientas poderosas de intercambio de ideas y resolución estructurada de problemas que se incluyen en Workspace.
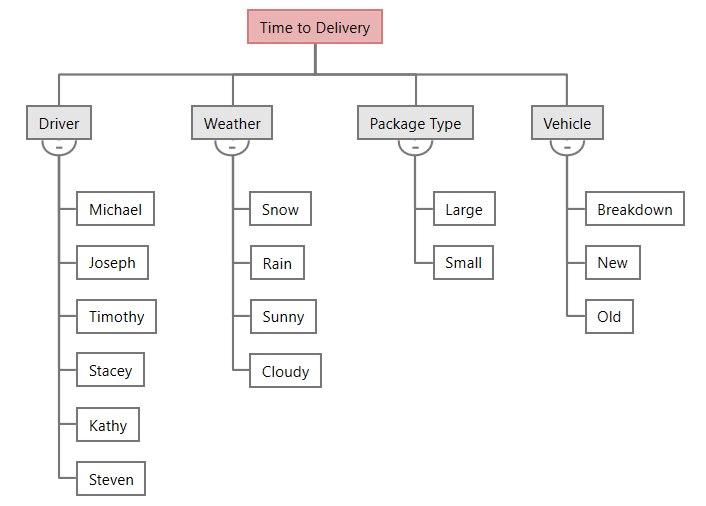
Cuantifique los impactos utilizando modelos predictivos...
En general, el modelado predictivo es útil para ayudar a hacer predicciones y comprender los factores que influyen en la respuesta. Al usar la Herramienta de aprendizaje automático de Minitab, no solo podemos ver el mejor modelo (en este caso, Random Forests®), sino que también podemos ver cómo se desempeñan otros modelos.
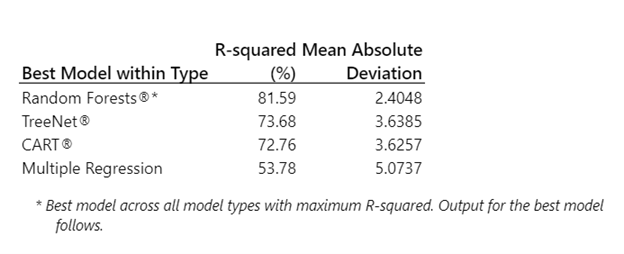
En este caso, el popular y tradicional método de regresión no solo tiene el peor rendimiento, sino que tampoco es muy preciso. Sin embargo, el modelo CART®, ideal para visualizar relaciones, funciona relativamente bien.
Aplicar mejoras...
Al observar el árbol de decisiones de CART a continuación, queda claro que las entregas más rápidas ocurren en condiciones soleadas con un vehículo más nuevo, mientras que los vehículos más antiguos que entregan en clima nevado tardan más. Esto proporciona la primera área a abordar para la mejora. Si bien es imposible controlar las condiciones climáticas, mantener una flota de vehículos más nuevos podría generar una mejora inmediata. Además, considerar el pronóstico del tiempo para una región específica del cliente podría proporcionar una mayor precisión al calcular y comunicar inicialmente los tiempos de entrega.
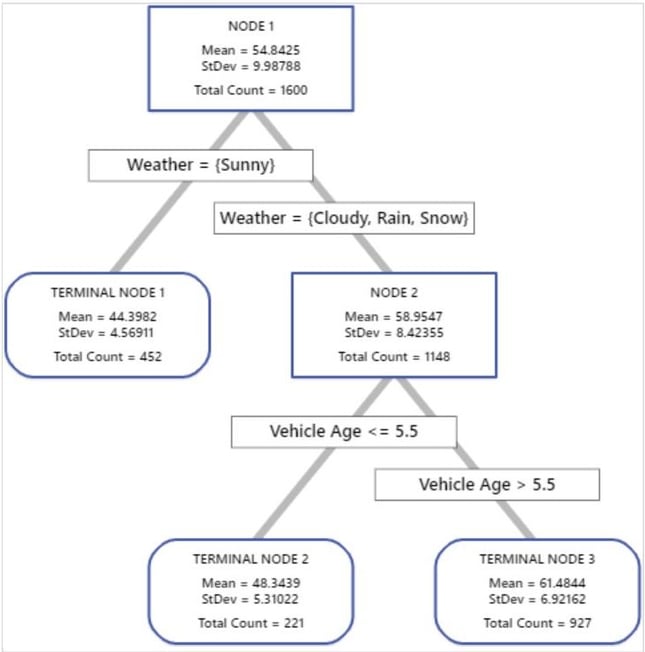
…Y poner en funcionamiento el modelo para predecir cuándo llegarán las entregas
Este análisis no solo puede ayudar a identificar áreas de mejora, sino que también puede ayudar a comunicarse con los clientes. Al considerar los factores disponibles y aprovechar el modelo Random Forests más preciso (según lo determinado por el aprendizaje automático), podemos poner en funcionamiento el modelo para comunicarnos automáticamente con los clientes. Uso de soluciones como Minitab Model Ops, a medida que se recopilan estos puntos de datos, el modelo puede calcular el tiempo de entrega estimado y comunicar automáticamente el tiempo a los clientes. Esto asegurará que sus clientes estén informados de manera oportuna, para que no adivinen cuándo llegará su paquete. A medida que mejora su desempeño, no solo puede superar las expectativas de sus clientes, sino que también puede continuar refinando su modelo predictivo para proporcionar una sincronización más precisa a los clientes en el futuro.
- Detalles
- Categoría: Comsol
- Visto: 5326
¡La presentación de resúmenes para la Conferencia COMSOL 2023 Munich ya está abierta! Presentar su trabajo en la conferencia es una oportunidad para obtener un reconocimiento inigualable de los profesionales de la simulación multifísica en todo el mundo. La conferencia también es una excelente manera de conectarse con colegas e intercambiar ideas sobre proyectos de investigación y desarrollo. Además, los presentadores se beneficiarán de que sus ponencias, carteles y diapositivas de presentación se publiquen en el sitio web de COMSOL.
Es fácil y rápido enviar un resumen para la Conferencia COMSOL. Selecciones su área temática:
| Electromagnetismo · Electromagnetismo de baja frecuencia · Óptica, fotónica y semiconductores · Física del plasma · Ingeniería de RF y Microondas |
Estructuras y acústica · Acústica y vibraciones · Geofísica y geomecánica · MEMS y Nanotecnología · Dispositivos piezoeléctricos |
Fluidos y calor · Dinámica de fluidos computacional (CFD) · Transferencia de calor y cambio de fase Microfluídica · Trazado de partículas |
Química · Diseño de baterías · Ingeniería de reacciones químicas · Corrosión y protección a la corrosión · Células de combustible y electrolizadores |
¿Listo para compartir su trabajo? Envíe un resumen (500 palabras o menos) que describa su uso innovador del software COMSOL®. Los resúmenes enviados antes de la fecha límite final de envío de resúmenes serán revisados por el comité del programa para su aceptación. Siga los cuatro pasos a continuación para completar el proceso de envío de resúmenes:
- Cree o inicie sesión en su cuenta COMSOL Access.
- Revise las pautas de envío de resúmenes para obtener instrucciones detalladas sobre cómo enviar su trabajo.
- Haga clic en el botón Mi conferencia para enviar su(s) resumen(es).
- Revise las instrucciones completas para la fecha de notificación del autor, que es cuando recibirá un correo electrónico que indica si su resumen ha sido aceptado junto con detalles adicionales de la presentación.
Para más detalles, visite: la web de la conferencia
- Detalles
- Categoría: Minitab
- Visto: 6376
Por Josué Zable.
Cuando las personas piensan en seguros, piensan en probabilidades, estadísticas y eficiencia. Es por eso que los clientes tienen aún menos paciencia con sus compañías de seguros cuando esperan una respuesta a una reclamación. Aunque las compañías de seguros son algunas de las empresas más hábiles para aprovechar el poder de los datos en el desarrollo de productos y perfiles de riesgo, a menudo hay oportunidades para aplicar la misma disciplina a las operaciones de su propia organización, particularmente a las interacciones con sus clientes. Minitab puede ayudar a las compañías de seguros a abordar las reclamaciones más rápido y mejorar su relación con los clientes.
Medir la velocidad del tiempo de respuesta a reclamaciones
El tiempo que se tarda en resolver un siniestro debe ser una medida clave para las compañías de seguros. Al ser la medida de la salida uno de los datos, debería ser bastante simple de recopilar y medir. Utilizando un conjunto de datos de muestra y algunas estadísticas descriptivas simples, el siguiente ejemplo muestra que el promedio (o la media) para el tiempo de resolución de la reclamación es de entre 54 y 55 días. Los datos también indican que el tiempo mínimo es de 40 días y el tiempo máximo es de 75 días, por lo que proporciona un rango de los tiempos más rápidos y más lentos que ayudan a establecer objetivos.

Establezca un objetivo y haga una lluvia de ideas sobre los posibles factores que afectan al rendimiento
Las reclamaciones lentas le cuestan a la organización no solo en términos de la experiencia del cliente, sino que cuanto más tiempo pasa sin resolverse una reclamación, mayor es la incertidumbre para la organización con respecto a las responsabilidades. Establezca un objetivo comercial estratégico para resolver las reclamaciones dentro de un período de tiempo determinado. En este ejemplo, establezcamos un objetivo realista de 50, lo que representa una mejora de ~10% en el tiempo de resolución.
A continuación, haga una lluvia de ideas sobre las posibles variables que podrían estar afectando el plazo de resolución de las reclamaciones. Esto podría ser cualquier cosa, desde el monto de la reclamación, el tipo de reclamación, el tipo de cliente o incluso el agente que maneja la reclamación. El siguiente diagrama muestra un ejemplo de un popular diagrama de espina de pescado, una de las muchas herramientas populares de intercambio de ideas y resolución estructurada de problemas.
Fishbone-Insurance-1.png
Utilice modelos predictivos para cuantificar los impactos...
En general, el modelado predictivo es útil para ayudar a hacer predicciones y comprender los factores que influyen en la respuesta. Al usar la Herramienta de aprendizaje automático de máquinas de Minitab, no solo podemos ver el mejor modelo (en este caso, Random Forests®), sino que también podemos ver cómo se desempeñan otros modelos.
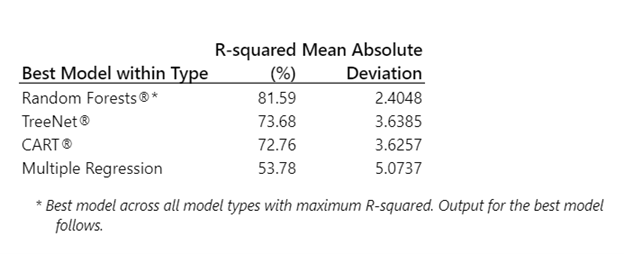
En este caso, el popular y tradicional método de regresión no solo tiene el peor rendimiento, sino que tampoco es muy preciso. Positivamente, el modelo CART®, ideal para visualizar relaciones, funciona relativamente bien.
Aplicar mejoras…
Al observar el árbol de decisiones de CART® a continuación, queda claro que los reclamos de automóviles toman la menor cantidad de tiempo para resolverse, mientras que los reclamos de robo y hurto toman más tiempo. Esto proporciona la primera área a abordar para la mejora. Mirando un paso más allá, está claro que la agente de casos Rebecca está luchando con estos casos en particular. Capacitar a Rebecca en estos casos particulares podría conducir a una mejora inmediata.
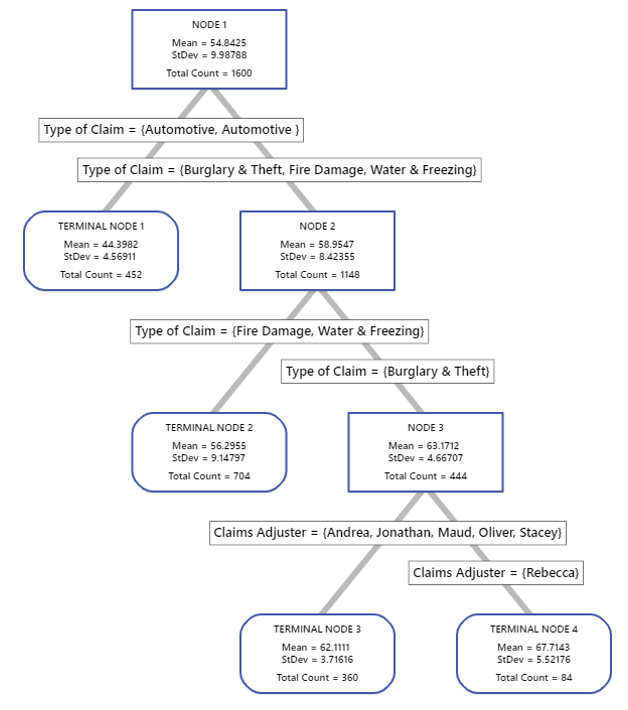
…¡Y operacionalice el modelo para comunicarse mejor con los clientes!
Este análisis no solo puede ayudar a identificar áreas de mejora, sino que también puede ayudar a comunicarse con los clientes. Al tomar los factores a mano y aprovechar el modelo Random Forests® más preciso (según lo determinado por el aprendizaje automático automático), podemos poner en funcionamiento el modelo para comunicarnos automáticamente con los clientes. Uso de soluciones como Minitab Model Ops, a medida que se recopilan estos puntos de datos, el modelo puede calcular el tiempo estimado para resolver el caso y comunicar automáticamente el tiempo a los clientes. Esto asegurará que las expectativas de los clientes se establezcan correctamente para que no se sientan decepcionados. A medida que mejora su desempeño, no solo puede superar las expectativas de sus clientes, sino que también puede continuar refinando su modelo predictivo para proporcionar una sincronización más precisa a los clientes en el futuro.
- Detalles
- Categoría: Comsol
- Visto: 5457
En la familia de productos de COMSOL Multiphysics, dentro del grupo de módulos sobre Electromagnetismo tenemos varios productos tales como AC/DC, RF, Wave Optics, Ray Optics, Plasma y Semiconductor. Dentro de ellas existen interfaces específicas para ciertos fenómenos de interés. Particularmente, el Semiconductor Module permite analizar el funcionamiento de dispositivos semiconductores al nivel físico fundamental. Las interfaces físicas dentro de él son las siguientes:
- Semiconductor (semi)
- Schrödinger Equation (schr)
- Schrödinger-Poisson Equation (schr)
- Semiconductor Optoelectronics, Beam Envelopes (ewbe)
- Semiconductor Optoelectronics, Frequency Domain (ewfd)
Una descripción sobre las ecuaciones que describen la física de cada interfaz se especifica a continuación.
Semiconductor Interface
La interfaz de Semiconductor da la posibilidad de describir a los electrones y huecos mediante la distribución de Maxwell-Boltzmann o Fermi-Dirac. Utiliza la Ecuación de Poisson para calcular el potencial eléctrico según la distribución de portadores de carga que existan. Los portadores de carga pueden ser electrones y huecos, así como también impurezas como donadores y aceptores. El transporte de los portadores, en términos de la densidad de corriente, se describe por medio del modelo de Drift-Diffusion (difusión-deriva), la cual tiene 3 términos principales: La respuesta de los portadores frente a i) un campo eléctrico, ii) un gradiente de concentración de portadores y iii) cambios de la temperatura. Bajo el nodo principal, se pueden incluir modelos de movilidad para electrones y huecos de tal modo de considerar las interacciones con la red cristalina L), impurezas (I), dispersión portador-portador (C), dispersión con impurezas neutras (N), saturación de velocidad en un campo intenso (E) y dispersión superficial (S). Como ejemplo, el modelo Arora toma en cuenta una combinación de estos procesos, siendo en modelo tipo LI.
Adicionalmente al sistema de ecuaciones, se añade una ecuación de continuidad debido a la recombinación de electrón-hueco y de la generación de pares electrón-hueco. La interfaz incluye los principales mecanismos de recombinación (Direct, Auger y Trap assisted recombination), y la posibilidad de definir una tasa de generación de pares electrón-hueco. Para extraer o inyectar portadores a un dispositivo se usan contactos metálicos. El contacto puede ser ideal óhmico o Schottky. Cuando se escoge Schottky, se pueden ingresar la Función de Trabajo (Metal Work Function), junto con los coeficientes de Richardson, e incluir un modelo para el tunelaje de electrones y huecos. Además, se pueden incluir velocidades de recombinación superficial (surface recombination velocities). Si, dentro del contacto Schottky se escoge User Defined, se puede ingresar la altura de la barrera (barrier height). Desde la versión 6.0 existe la posibilidad de activar el campo Contact Resistance (en la sección Terminal del nodo de Metal Contact). Con ello se puede especificar el valor de la resistencia específica de contacto (specific contact resistivity).
Desde el punto de vista numérico, se proporcionan dos métodos: el método del volumen finito y el método de elementos finitos estabilizado por mínimos cuadrados de Galerkin [1].
Schrödinger y Schrödinger-Poisson interfaces
Por un lado, la interfaz de la ecuación de Schrödinger resuelve la ecuación de Schrödinger para problemas generales de mecánica cuántica, así como para las funciones de onda de electrones y huecos en semiconductores cuánticos confinados bajo el supuesto de la aproximación de la función envolvente (envelope function).
Por otro lado, la interfaz multifísica de la ecuación de Schrödinger-Poisson combina la ecuación de Schrödinger y la electrostática (es) para modelar portadores de carga en sistemas cuánticos, también con confinamiento. El potencial eléctrico contribuye al término de energía potencial en la ecuación de Schrödinger. Una suma ponderada de las densidades de probabilidad de los eigenstates de la ecuación de Schrödinger contribuye a la densidad de carga espacial en la electrostática. Cuando se selecciona la interfaz de Schrödinger-Poisson, se añade la interfaz de Electrostatics (es) así como un nodo de multifísica para el acoplamiento.
Una descripción teórica de la física de esta interfaz junto con un ejemplo se encuentra disponible en el Blog de COMSOL [2]. Allí se muestra que la ecuación Schrödinger-Poisson permite simular potadores de cargas confinados en quantum wells, nanowires y dots. El ejemplo descrito se trata de un nanowire de GaAs para demostrar la utilización de la interfaz.
Semiconductor Optoelectronics, Beam Envelopes y Frequency Domain
En este caso, se combinan la interfaz Semiconductor con la interfaz Electromagnetic Waves, Beam Envelopes (ewbe) o Frequncy DOmain (ewfd). El acoplamiento se produce a través de la función Transiciones ópticas. Para ello, existe el nodo Optical Transitions el cual añade un término de generación de emisión estimulada (apropiado para materiales de banda prohibida directa) en los dominios de la interfaz Semiconductor. Este término es proporcional a la intensidad óptica en la interfaz “ewbe” o en la interfaz “ewfd”. Además, se tiene en cuenta la emisión espontánea (para materiales de banda prohibida directa). El efecto de la adsorción o emisión de luz se explica por un cambio correspondiente en la permitividad compleja o el índice de refracción en la interfaz de óptica ondulatoria. Estas interfaces se utilizan para modelar dispositivos como fotodiodos, diodos emisores de luz y diodos láser sin pozos cuánticos en materiales de banda prohibida directa. Un ejemplo práctico se encuentra disponible en [3], donde se modela y simula un fotodiodo PIN de GaAs. El estudio en el dominio de la frecuencia permite visualizar las características espectrales del dispositivo.
Observaciones finales
El módulo proporciona una interfaz fácil de usar para analizar y diseñar dispositivos semiconductores, simplificando en gran medida las tareas de simulación del dispositivo en la plataforma de COMSOL. Así, el módulo Semiconductor es útil para simular una gran variedad de dispositivos prácticos. La librería de modelos integrada contiene una suite de modelos diseñados para proporcionar instrucciones sencillas y demostrar cómo utilizar la interfaz para simular sus propios dispositivos. Semiconductor Module es particularmente adecuado para simular transistores incluyendo transistores bipolares, de efecto de campo metal-semiconductor (MESFET), efecto de campo metal-oxido-semiconductor (MOSFET), diodos Schottky, tiristores, uniones P-N y células solares. Dentro de la librería de aplicaciones, existen diversos ejemplos para simular dispositivos como transistores bipolares, transistores de efecto de campo metal-semiconductor (MESFET), transistores de efecto de campo metal-oxido-semiconductor (MOSFET), diodos Schottky, tiristores y uniones P-N. También existen aplicaciones como una célula solar acoplado con Ray Optics, donde se puede escoger la locación y considerar el recurso solar local [4]. Otro recurso disponible para aprender sobre este módulo se encuentra en el Webinar realizado por Addlink [5].
Referencias
[1] https://www.comsol.com/semiconductor-module
[2] https://www.comsol.com/blogs/self-consistent-schrodinger-poisson-results-for-a-nanowire-benchmark.
[3] https://www.comsol.com/model/gaas-pin-photodiode-19705
[4] https://www.comsol.com/model/si-solar-cell-with-ray-optics-36201
[5] https://www.addlink.es/eventos/comsol/webinar-taller-introduccion-practica-a-la-simulacion-de-dispositivos-semiconductores-con-comsol-multiphysics
- Detalles
- Categoría: ChemOffice
- Visto: 7190
La versión 22.2 de ChemOffice y ChemDraw contiene mejoras y ampliaciones compatibles con los enlaces de hidrógeno y HELM. Entre las nuevas características destacan:
- Soporte expandido de enlaces de Hidrógeno en las áreas de percepción y manejo. Los enlaces de hidrógeno son ahora exportables a 3MF y son gestionados en la depuración 3D. Además, los enlaces de hidrógeno se distinguen ahora como entidades distintas para la detección de anillos. Por último, se conservan en la importación/exportación de un proceso de edición en ChemDraw Desktop.
- Nuevas Modalidades (HELM). Los monómeros de base de ARN se colorean ahora en función de su análogo natural cuando se representan en documentos de monómeros gráficos de secuencias en ChemDraw.
Otras novedades que ofrece la versión 22 son:
- Eliminada la instalación en paralela de ChemDraw/ChemOffice.
- Añadido el soporte para Conflex 9 Rev B en ChemDraw 3D.
- Disponible una versión de 64 bits de Chem3D en la instalación estándar de ChemOffice.
Además, ChemDraw JS 22.2 también se liberará con este paquete. ChemDraw JS 22.2 contiene varias actualizaciones de rendimiento para mejorar el renderizado y el manejo de datos, así como actualizaciones para permitir el soporte de imágenes multiplataforma.
El resto de mejoras y novedades pueden consultarse en la página de ChemDraw 22 y ChemOffice 22.