- Detalles
- Categoría: Systat Software
- Visto: 4981
SigmaPlot es un paquete de software de análisis estadístico y gráfico, de datos científicos, fácil de utilizar para investigadores, científicos e ingenieros que necesiten crear los gráficos precisos, con calidad de publicación, que mejor comuniquen sus resultados de investigación para presentaciones, publicaciones técnicas y la web.
Junto con su ajuste de curvas avanzado, un lenguaje de programación basado en vectores, capacidad de macros y más de 50 tests estadísticos frecuentemente utilizados, SigmaPlot también proporciona más de 100 tipos de gráficos diferentes 2D y 3D, de los que uno puede escoger un amplio rango de opciones de graficado como escalas de ejes técnicos, múltiples ejes, múltiples gráficos 3D intersectando y mucho más.
SigmaPlot ahora incluye SigmaStat que es una herramienta perfecta para visualizar y comprender estadísticos básicos y avanzados.
SigmaPlot ofrece:
- Análisis estadístico consultivo completo
- Capacidad de graficado técnico galardonada
- Análisis de datos potente y fácil de usar
- Capacidad de personalizar cada elemento del gráfico
- Gráficos precisos con calidad de publicación
- Capacidad de publicar tu trabajo en cualquier sitio
Ultimas actualizaciones:
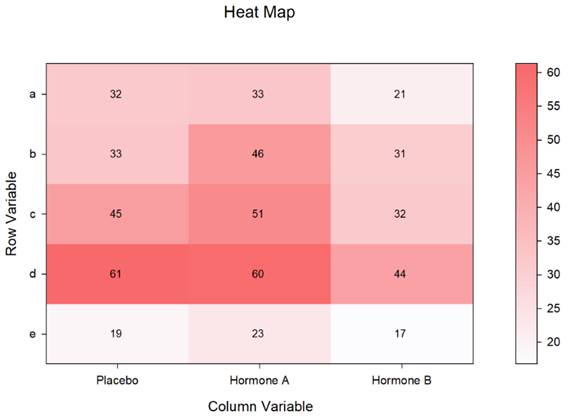
- Incluye una nueva Macro de Mapa de Calor
- Elimina todas las dependencias de viejos redistribuibles al eliminar Lead Tools y utilizar Windows Graphics Device Interface + (GDI+) para exportación de gráficos
- Utiliza el último gestor de licencias Sentinel License Manager que es compatible con el último Microsoft Server 2022
- Utiliza un servicio de licenciamiento alojado para una activación y validación de licencia perfeccionada
- Tiene un nuevo y renovado gestor de cintas que mejora la ya encomiable experiencia de usuario en SigmaPlot ©2022
- Detalles
- Categoría: MapleSim
- Visto: 5034
El Dr. Orang Vahid, Director de Servicios de Ingeniería de Maplesoft, analiza el uso de la simulación a nivel de sistema para resolver problemas de diseño de manejo de bobinas y cintas, en un artículo detallado de la última edición de Converting Quarterly de la Association for Roll-to-Roll Converters.
Léalo en línea a través del enlace inferior.
- Detalles
- Categoría: Minitab
- Visto: 3958
Por Josué Zable
En el negocio petrolero hay dos cosas que tienen en común una gran corporación multinacional, una compañía petrolera nacional, una compañía petrolera independiente, una compañía de servicios petroleros y un contratista independiente:
- Todos quieren optimizar rápidamente su producción con el menor coste.
- Todos se enfrentan a desafíos que crean ineficiencias en la perforación y que retan a su capacidad para ejecutar su objetivo.
¿POR QUÉ LAS INEFICIENCIAS?
Puede haber varias razones por las que una compañía petrolera puede experimentar ineficiencias en las operaciones de perforación.
Desafíos geológicos
Las operaciones de perforación pueden verse afectadas por formaciones geológicas complejas, como formaciones de roca dura, zonas de alta presión o condiciones inesperadas del subsuelo. Estos desafíos pueden conducir a un progreso de perforación más lento, un mayor desgaste en el equipo de perforación y la necesidad de mantenimiento o reemplazo frecuente del equipo.
Limitaciones del equipo
Los equipos de perforación ineficientes u obsoletos pueden dificultar las operaciones de perforación. El mal funcionamiento del equipo, la potencia o el par inadecuados, la velocidad de perforación limitada o la capacidad insuficiente de circulación del fluido de perforación pueden contribuir a las ineficiencias en el proceso de perforación.
Planificación y ejecución inadecuadas
La mala planificación y coordinación puede conducir a operaciones de perforación ineficientes. El diseño de pozos inexacto, la selección inadecuada de técnicas de perforación, las medidas inadecuadas de estabilidad del pozo y la supervisión y comunicación inadecuadas pueden provocar demoras, mayores costes y un rendimiento de perforación subóptimo.
Propiedades subóptimas del fluido de perforación
Las propiedades del fluido de perforación, como la viscosidad, la densidad, la lubricidad y la estabilidad, juegan un papel crucial en la eficiencia de la perforación. El uso de fluidos de perforación inapropiados o mal formulados puede causar problemas como tubería atascada, atascamiento del diferencial, mala limpieza del pozo o desgaste excesivo de las herramientas de perforación, lo que reduce la eficiencia de la perforación.
Cumplimiento normativo y de seguridad
Las estrictas normas ambientales y de seguridad en la industria del petróleo y el gas a veces pueden agregar complejidad a las operaciones de perforación. Las empresas que luchan por mantener el cumplimiento o no implementan prácticas de seguridad efectivas pueden experimentar retrasos o interrupciones en las actividades de perforación, lo que genera ineficiencias.
EL ANÁLISIS DE DATOS PUEDE IDENTIFICAR ÁREAS DE MEJORA PARA REDUCIR Y ELIMINAR LAS INEFICIENCIAS
La recopilación y el análisis de datos relevantes durante las operaciones de perforación pueden ayudar a identificar las ineficiencias. Sin él, la empresa puede perder optimizaciones potenciales, mejores prácticas y lecciones aprendidas que podrían mejorar la eficiencia de la perforación.
Como ejemplo, imagínese que una compañía petrolera quiere evaluar y mejorar su proceso de perforación en términos de velocidad de perforación, específicamente el tiempo que lleva perforar a cierta profundidad. El objetivo de la empresa es perforar hasta cierta profundidad en 12 horas. La empresa ha recopilado datos sobre tiempos de perforación para una muestra de pozos perforados en un campo en particular.
Recopila las horas de tiempo de perforación de 30 pozos de la siguiente manera: 12.5, 10.9, 11.8, 13.2, 11.5, 12.1, 11.3, 12.7, 13.5, 14.2, 10.8, 12.0, 13.1, 12.3, 11.6, 12.8, 11.9, 12 .4, 13.0 , 12.6, 11.2, 13.3, 12.9, 12.6, 11.7, 13.8, 12.5, 12.2, 10.7, 11.4.
Las estadísticas descriptivas y las visualizaciones pueden generar conocimientos
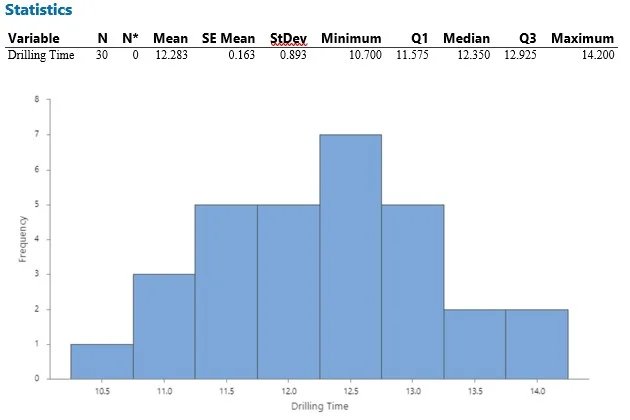
Si bien este es un primer paso básico, al calcular ciertas estadísticas descriptivas, como la media, la mediana, la desviación estándar y el rango, se puede obtener una descripción general de los datos e identificar cualquier valor atípico o patrón inusual.
Según los datos de nuestro ejemplo, la media y la mediana están entre 12 y 12,5 horas, lo que indica que nuestros datos son simétricos o se ajustan a una distribución normal. Mirando un histograma, puede verse una imagen de nuestra distribución, incluida la identificación de valores atípicos.
Sin embargo, en promedio, la empresa no cumple con sus especificaciones de 12 horas.
Hay dos oportunidades de mejora: Primero, identificar los pozos de petróleo que tomaron más de 12 horas puede resaltar las ineficiencias que existen. En segundo lugar, al averiguar qué salió bien en los pozos de petróleo que tomó menos tiempo que la media y la mediana, existe la oportunidad de aplicar esos conocimientos a otros pozos.
Si bien existen claramente oportunidades de mejora, antes de jugar con nuestro proceso, comprendamos mejor si es estable o no y si es capaz de replicar los resultados.
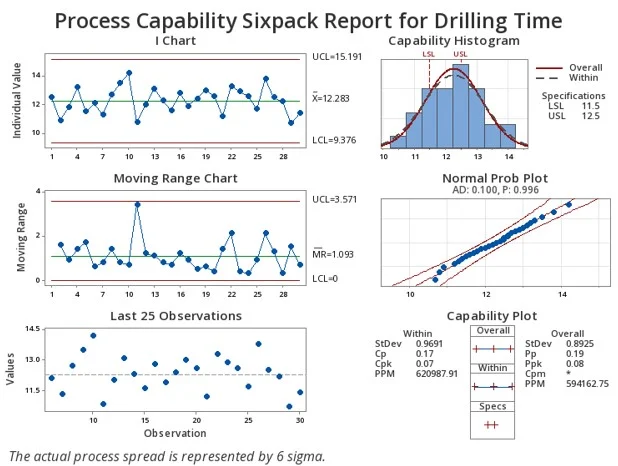
El análisis del proceso puede indicar si el proceso es estable y capaz de cumplir los objetivos de manera consistente
Al utilizar el Análisis de capacidad seis en uno propiedad de Minitab, con un rápido clic del mouse se pueden ver gráficos de control que resaltan que el proceso es estable. Desafortunadamente, tanto nuestro Cpk como nuestro Ppk están cerca de cero, lo que destaca que nuestro proceso no es capaz. Para que un proceso sea capaz, su Cpk y Ppk deben ser al menos superiores a 1,33, idealmente un valor de 2,0 o superior cuando sea posible.
Comprender esto es fundamental para la mejora; nos informa que nuestro proceso no puede cumplir con las especificaciones. En lugar de tratar de hacer un cambio en uno de los pozos, deberíamos evaluar todo nuestro proceso de perforación.
¿QUE SIGUE? ¡COMIENZA UN PROYECTO DE MEJORA!
Comprender que un proceso necesita mejorar es el primer paso en un ejercicio de mejora continua. Con herramientas de planificación y ejecución de proyectos, como las que se encuentran en Minitab Workspace, puede planificar y evaluarse el proceso. A partir de ahí, se debe recopilar datos para el análisis y usar estadísticas y análisis predictivos para ayudar a identificar las causas fundamentales del problema.
- Detalles
- Categoría: Comsol
- Visto: 13531
Felix Savart, cirujano y físico francés nacido en junio 1791, formuló la Ley de Biot-Savart
Desde el punto de vista histórico, el mes pasado fue importante para la teoría electromagnética. Se trata de la Ley de Biot Savart, la cual establece que: La densidad de flujo magnético infinitesimal asociado es proporcional al elemento de longitud de circuito, la corriente que recorre cada elemento e inversamente proporcional al cuadrado de la distancia de ese punto. La dirección del campo magnético está en la dirección de dl×r. Ver Ec. 1, donde μ0 es la permeabilidad del vacío, I es la corriente que fluye a través del elemento de camino dl y r es la posición en dicho camino (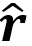 vector unitario).
vector unitario).
Ec.1
La ley es válida en la aproximación magnetostática, y coherente tanto con la ley circuital de Ampère como con la ley de Gauss para el magnetismo [1]. Recibe su nombre de Jean-Baptiste Biot y Félix Savart, que descubrieron esta relación en 1820. Así, la ley de Biot-Savart puede utilizarse para calcular el campo magnético resultante de una distribución de corriente eléctrica.
Otras características notables sobre La ley de Biot-Savart son que es exactamente similar a la ley de Coulomb en electrostática y es relevante para conductores muy pequeños que transportan corriente. Para una distribución simétrica de corriente, dicha ley es aplicable. Ejemplo, la Ley de Biot Savart se puede utilizar para evaluar la respuesta magnética a nivel molecular o atómico. Por otra parte, se puede usar para evaluar la velocidad en la teoría aerodinámica inducida por la línea de vórtice. A continuación, hablamos sobre la Ley de Biot-Savart en el Electromagnetismo y su conexión con las Leyes de Maxwell. Adicionalmente ponemos énfasis en ejemplos realizados en COMSOL Multiphysics, donde se pone al campo magnético como protagonista.
Conexión con otras leyes en Electromagnetismo
Ley de Ampere
¿Cuál es la relación entre la Ley de Biot Savart y las Ecuaciones de Maxwell? [2], siendo las ecuaciones de Maxwell un conjunto de ecuaciones fundamentales que rigen el comportamiento de los campos eléctricos y magnéticos. En efecto, se puede derivar a partir de Maxwell, concretamente de la Ley de Ampere, que establece una conexión entre una corriente eléctrica y el campo magnético que genera.
Aunque la Ley de Biot Savart y la Ley de Ampere abordan los campos magnéticos, su enfoque y aplicabilidad difieren. Por ejemplo, la Ley de Biot Savart es más útil para calcular campos magnéticos debidos a bucles de corriente o conductores irregulares portadores de corriente. En cambio, la Ley de Ampere se adapta mejor a geometrías simétricas y corrientes estacionarias.
Ley de Faraday
La relación entre la Ley de Biot Savart y la Ley de Faraday es intrigante. Por un lado, la Ley de Biot Savart se refiere al campo magnético generado por una corriente. Por otro lado, la Ley de Faraday trata de la fuerza electromotriz (FEM) inducida en un conductor debido a un campo magnético cambiante. Juntas, estas leyes forman la base de la inducción electromagnética, que sustenta el funcionamiento de generadores eléctricos, transformadores e inductores.
La teoría electromagnética sólo estaría completa si se abordara el concepto de campo eléctrico. Al igual que los campos magnéticos, los campos eléctricos son conceptos fundamentales del, originados por las cargas eléctricas. La Ley de Coulomb rige la interacción entre cargas eléctricas, estableciendo paralelismos con la Ley de Biot Savart, que trata de los campos magnéticos generados por corrientes eléctricas.
Algunas aplicaciones
Las aplicaciones prácticas de la Ley de Biot Savart son abundantes, desde el diseño y análisis de electroimanes y generadores hasta la determinación del momento magnético de un bucle de corriente, parámetro esencial en magnetostática. La ley también ha contribuido significativamente al desarrollo de tecnologías como la resonancia magnética (RM), los aceleradores de partículas y los dispositivos de almacenamiento magnético.
La versatilidad de la Ley de Biot Savart queda patente en su capacidad para calcular campos magnéticos de distintas geometrías. Desde un hilo recto o un solenoide hasta configuraciones más complejas como bobinas toroidales o en forma de silla de montar, esta ley es una herramienta fiable para comprender el comportamiento de los campos magnéticos en distintos escenarios.
Electromagentismo en COMSOL Multiphysics
COMSOL Multiphysics posee diferentes módulos que se basan en su totalidad o bien están relacionados con fenómenos electromagnéticos. Tales módulos son AC/DC, RF, Wave Optics, Ray Optics, Plasma and Semiconductor [3]. No obstante, el módulo por excelencia y que permite estudiar muchos casos o situaciones distintas para dispositivos electromagnéticos es el módulo AC/DC. A continuación, revisamos algunos ejemplos para visualizar la utilidad del software en esta área.
Ejemplo 1
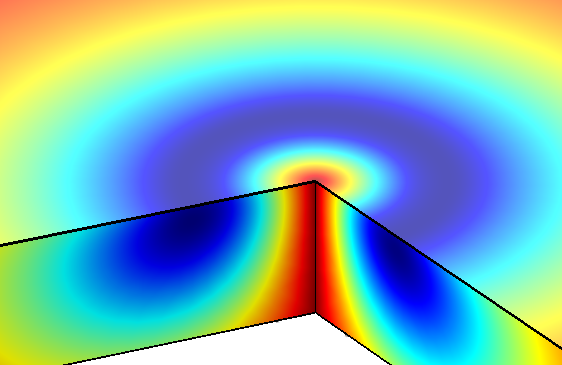
Este modelo se trata de una corriente variable en el tiempo que induce un campo magnético variable en el tiempo [4]. El campo magnético induce corrientes en los conductores vecinos. Las corrientes inducidas se denominan corrientes parásitas. En este modelo, el fenómeno se ilustra mediante una simulación de campo armónico en el tiempo, así como un análisis transitorio, en el que se estudian las corrientes de Foucault resultantes de la conexión de la fuente. Se tienen dos bobinas portadoras de corriente sobre una placa de cobre. Las bobinas están rodeadas de aire y hay un pequeño entrehierro entre ellas y la placa metálica. La fuente externa se aplica como densidad de corriente, pero la densidad de corriente total en las bobinas sólo se obtiene teniendo en cuenta las corrientes inducidas. El caso armónico en el tiempo muestra el efecto Skin. Esto quiere decir que la densidad de corriente es alta en la proximidad de la superficie y disminuye rápidamente en el interior del conductor.
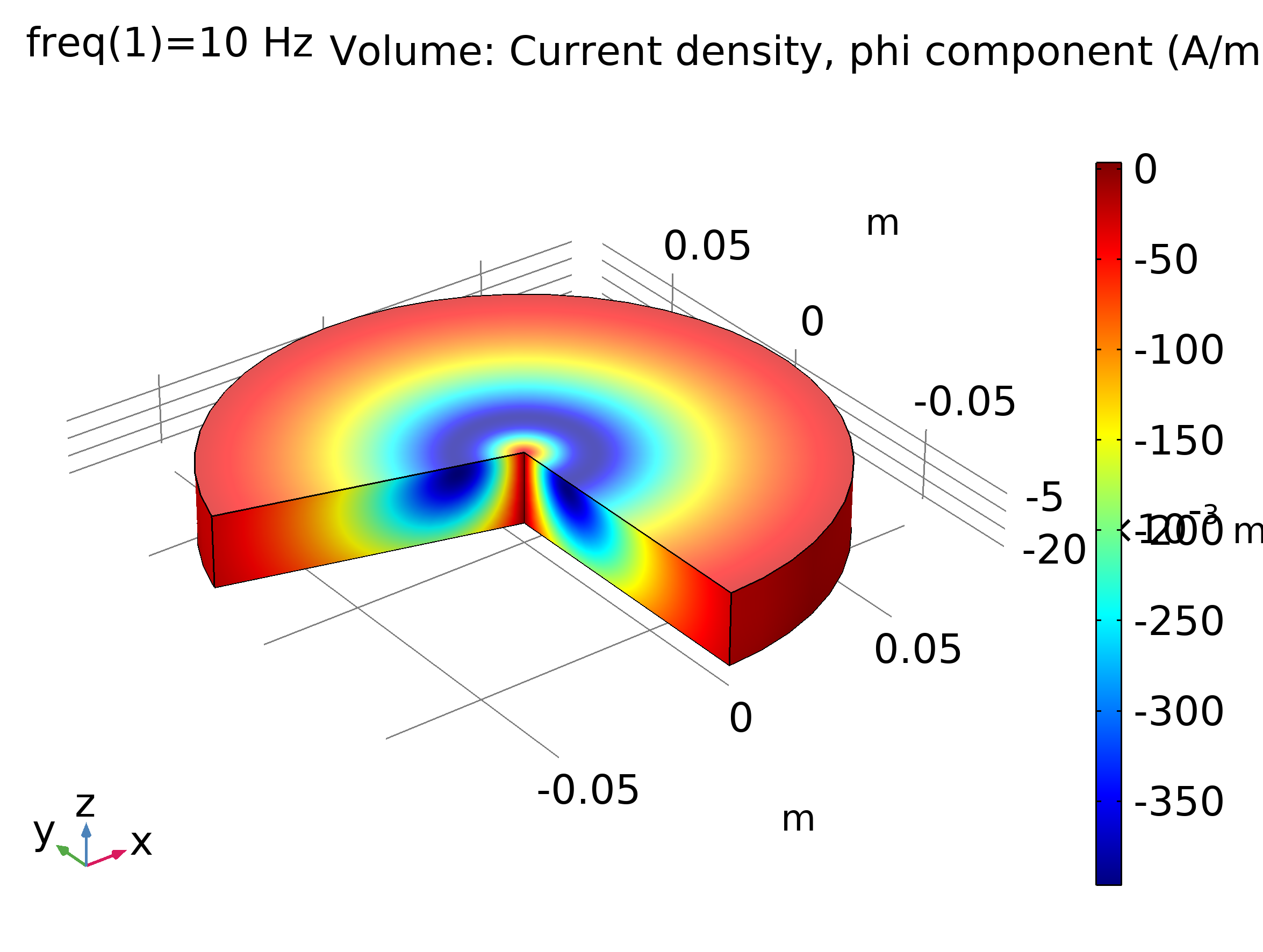
Fig. 1. Componente angular Phi de la densidad de corriente a una frecuencia de 10 Hz. Ver modelo en [4].
Ejemplo 2
El modelo se llama An Electrodynamic Levitation Device – el cual trata el acoplamiento dinámico electromagnético y la dinámica de cuerpos rígidos [5]. Una fuerza de levitación electrodinámica se produce por las corrientes inducidas cuando un disco conductor se coloca por encima de dos bobinas concéntricas que llevan corrientes variables en el tiempo en direcciones opuestas. Se resuelve la dinámica del disco levitante y se compara con los datos medidos en la bibliografía.
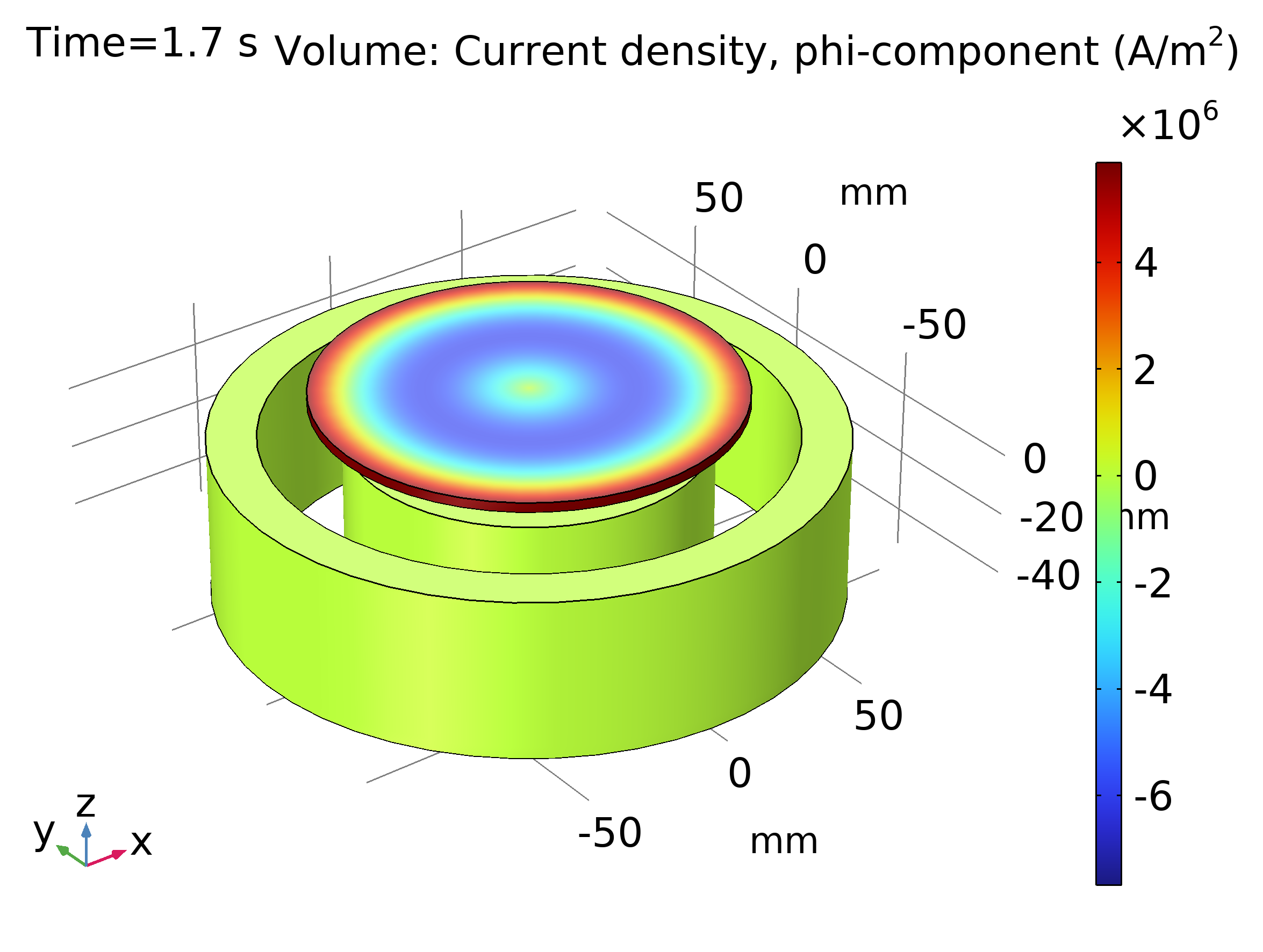
Fig. 2. Componente angular Phi de la densidad de corriente a los 1.7 s en el dispositivo. Ver modelo en [5].
Ejemplo 3
Otro modelo relevante para aprender es el de una máquina de transporte marítimo que se desplaza por la superficie o bajo el agua como un submarino, dando lugar a perturbaciones locales detectables en el campo magnético terrestre [6]. Dichas perturbaciones pueden utilizarse para activar sistemas de armamento. La firma magnética de un submarino puede reducirse generando un campo magnético que se contrapone de intensidad y dirección adecuadas basado en el conocimiento previo de las propiedades magnéticas del submarino.
Este modelo demuestra una poderosa técnica en este tipo de modelado al tratar la cubierta metálica como caras 2D incrustadas en una geometría 3D. Así, se requieren mallas de 2D comparativamente más sencillas que el caso 3D. A continuación, se resuelve una proyección tangencial de la ecuación 3D en la malla de caras 2D.
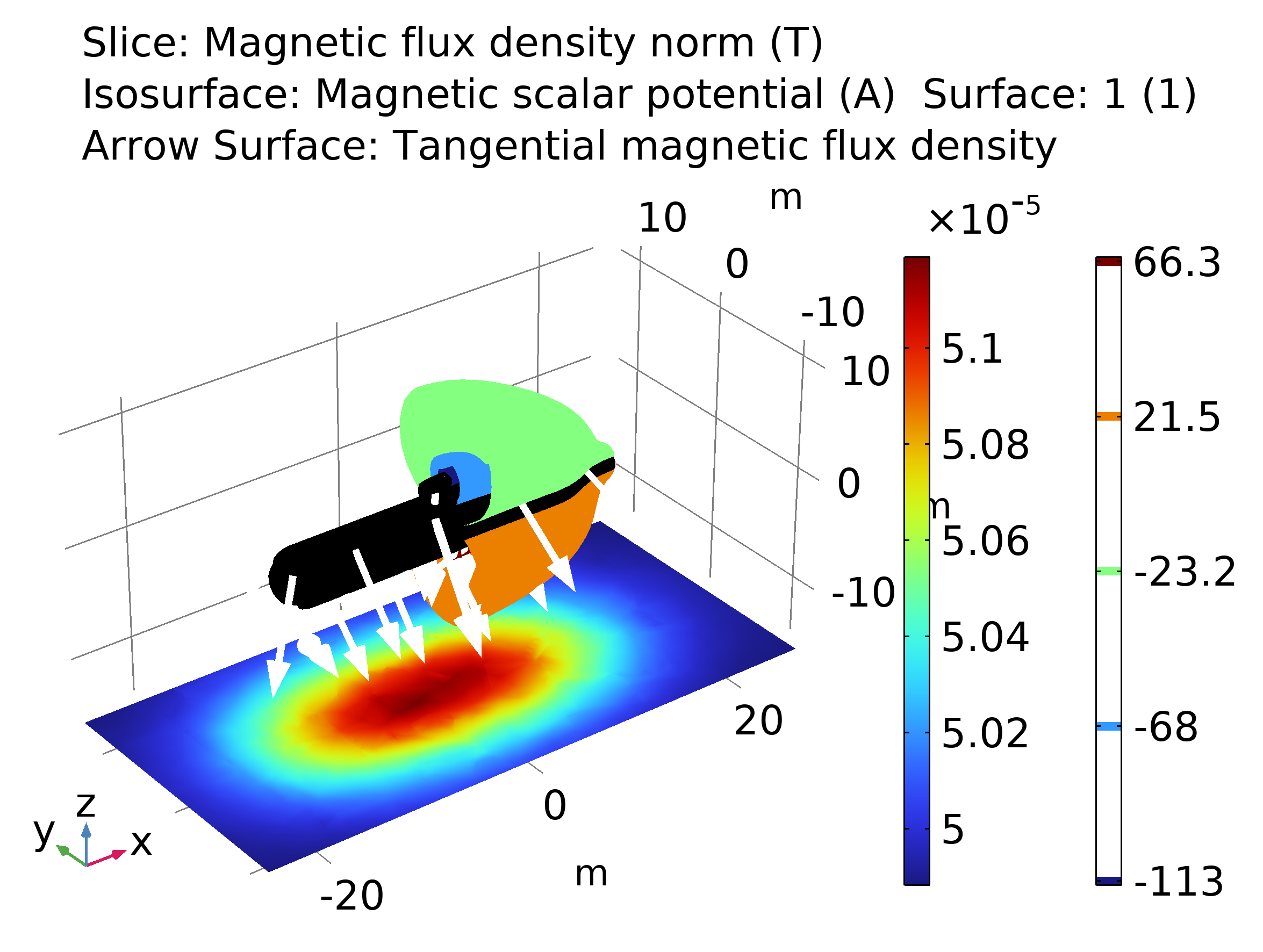
Fig. 3. Magnitud de la densidad de flujo magnética, potencial escalar magnético y componente tangencial de la densidad de flujo magnética para el submarino. Ver modelo en [6].
Referencias
[1] https://www.comsol.com/multiphysics/electromagnetics
[2] https://iopscience.iop.org/article/10.1088/0305-4470/20/8/022/pdf
[3] https://www.comsol.com/blogs/computational-electromagnetics-modeling-which-module-to-use/
[4] https://www.comsol.com/model/induction-currents-from-circular-coils-124
[5] https://www.comsol.com/model/an-electrodynamic-levitation-device-14221
[6] https://www.comsol.com/model/magnetic-signature-of-a-submarine-291
- Detalles
- Categoría: Maple
- Visto: 9595
Cómo le ayuda la tecnología a asistir a sus alumnos
Las matemáticas son importantes, tanto para nuestro mundo en general como para el futuro éxito individual de sus alumnos. Es por eso que, como profesores, se esfuerzan incansablemente por ayudar a sus estudiantes a comprender y trabajar con las matemáticas. Es un trabajo importante y gratificante, pero también es una tarea con grandes desafíos que se vuelve especialmente difícil cuando crece el tamaño de las clases, se multiplican las distracciones y se siguen sintiendo los efectos de la pérdida de aprendizaje. Afortunadamente, la tecnología adecuada puede actuar como su asistente, brindando un mayor retorno de la inversión de tiempo y energía que dedica a la enseñanza y ayudándolo a ayudar a sus estudiantes a tener éxito.
En este documento técnico, examinaremos siete desafíos de los más comunes a los que se enfrentan los instructores que enseñan matemáticas u otros cursos que hacen uso de las matemáticas, como ingeniería, física, química, negocios y economía. Para cada desafío, mostraremos ejemplos de cómo Maplesoft Mathematics Suite, una colección de soluciones de software de Maplesoft, puede proporcionar visualizaciones esclarecedoras, comentarios instantáneos, ejemplos motivadores, exploraciones prácticas y otros soportes que pueden ayudarle a conquistar ese desafío. Para ilustrar estos ejemplos, proporcionamos capturas de pantalla y videoclips cortos tomados con una variedad de productos de la Suite.
Los Desafíos
Cuando se trata de la formación matemática, ya sea que se esté enseñando un curso de matemáticas o un curso basado en las mismas, los siete desafíos más comunes a los que se enfrentan los profesores son:
- Involucrar a los estudiantes que se aburren o distraen fácilmente
- Motivar a los estudiantes que no le ven la utilidad
- Superar la ansiedad matemática
- Inculcar una verdadera comprensión en los estudiantes que solo están siguiendo los movimientos
- Proporcionar suficientes oportunidades para la práctica
- Evaluar el progreso en un mundo donde es fácil buscar respuestas
- Manejar diferentes niveles de preparación para el curso
No puedes gestionar estos problemas invirtiendo más tiempo en tus clases. ¿De dónde sacarías esas horas? Pero la tecnología matemática puede ayudar en cada una de estas áreas.
Desafío 1: Involucrar a los estudiantes que se aburren o distraen con facilidad
Los estudiantes tienen muchas demandas en su atención, incluso durante la clase. Mucho de lo que hay en sus teléfonos y computadoras portátiles está diseñado específicamente para atraerlos cuando lo que se necesita es que presten atención, y para muchos estudiantes, "un montón de ecuaciones" no es exactamente lo más apasionante.
Pero las matemáticas pueden cobrar vida. Puede ser algo visual. Puede ser interactivo. Puede ser divertido perder el tiempo, solo para ver qué sucede. A veces incluso puede inspirar a los estudiantes con sus grandes posibilidades. Pero para eso, necesitas algo más que una página estática. Necesita algo dinámico, con visualizaciones esclarecedoras e interactividad realmente significativa.
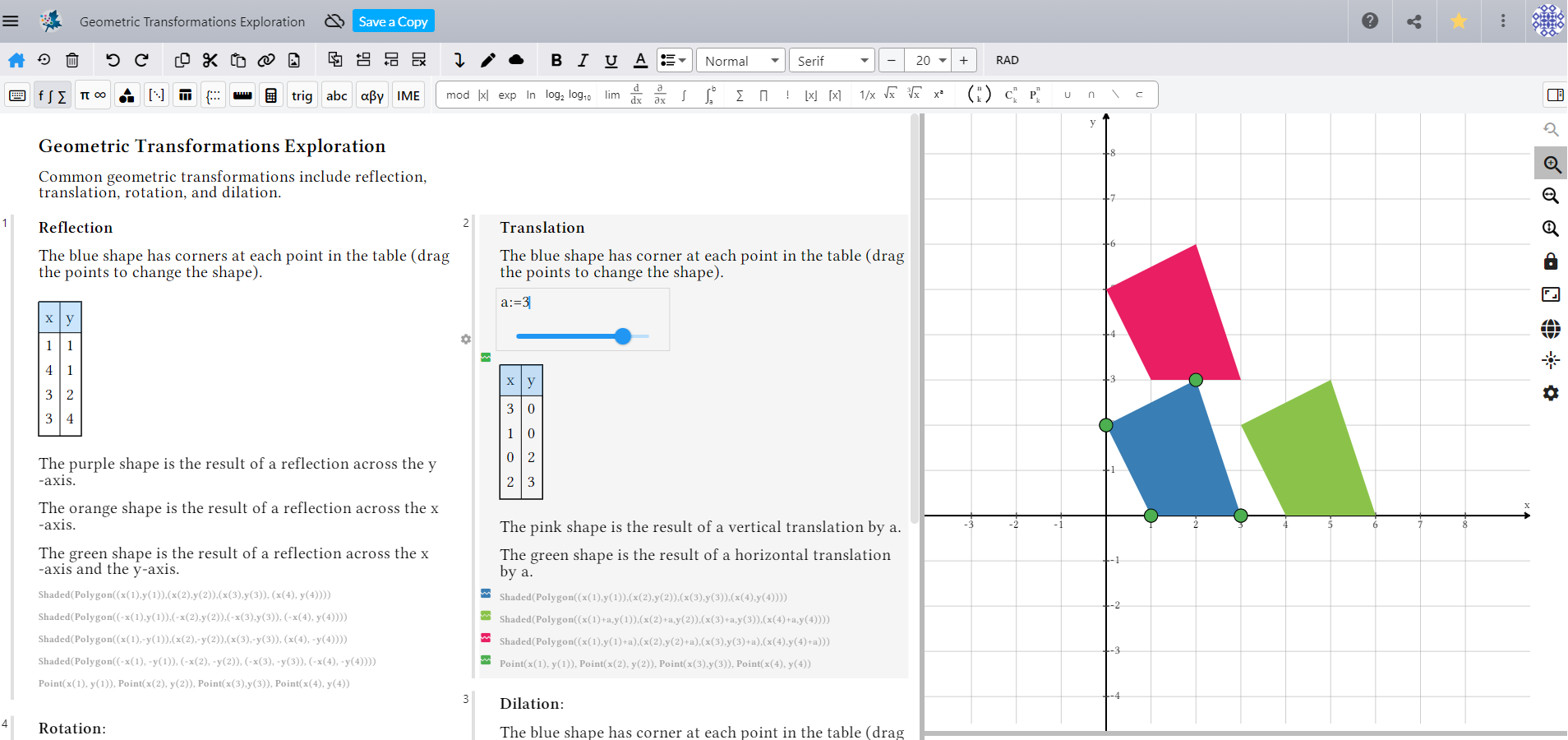
Ejemplo: Transformaciones GeométricasEn este ejemplo que demuestra transformaciones geométricas, los estudiantes pueden realizar reflexiones, rotaciones y dilataciones por sí mismos y ver los resultados al instante. Por ejemplo, pueden crear una forma y verla reflejada en el eje X y el eje Y, traducir una forma horizontal y verticalmente moviendo un control deslizante o mover un control deslizante diferente para establecer un factor de dilatación y ver los resultados. |
|
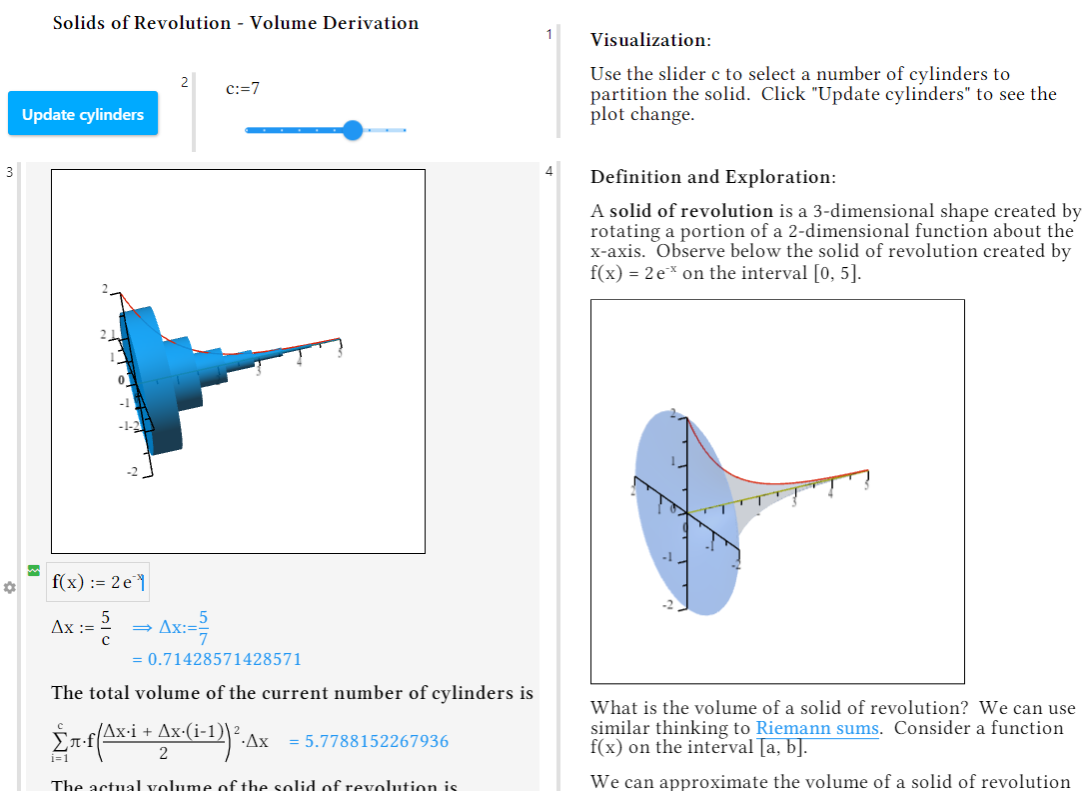
Ejemplo: Volumen de Sólidos de RevoluciónLos estudiantes a menudo luchan por visualizar sólidos de revolución, y los instructores se han convertido en pretzels tratando de transmitir el concepto. En este ejemplo, los estudiantes pueden ver cómo se rota la curva 2D para formar la forma 3D y luego rotar la imagen resultante para obtener una buena vista desde diferentes ángulos. Pueden ver cómo los cilindros se aproximan a la forma y aumentar el número de cilindros para ver visualmente, así como numéricamente, cómo mejora la aproximación. |
|
Desafío 2: Motivar a los estudiantes que no le ven la utilidad
Sin duda habrá escuchado muchas variaciones de "¿Pero para qué sirve esto?" en su clase. Algunos estudiantes pueden estar contentos de aprender matemáticas por las matemáticas, pero la mayoría quiere saber por qué necesitan aprender lo que se les está enseñando. ¿Para qué sirve? ¿Por qué debería importarle a alguien?
Por supuesto, las matemáticas se usan en todas partes, y las aplicaciones del mundo real contribuyen en gran medida a motivar a los estudiantes. Desafortunadamente, la mayoría de los ejemplos realistas son demasiado complicados para resolverlos a mano en clase y, a veces, involucran matemáticas que los estudiantes aún no han aprendido. Pero con la tecnología adecuada, puede presentarse a los alumnos aplicaciones motivadoras de los conceptos que se necesita que aprendan, sin que nadie se atasque en los cálculos.
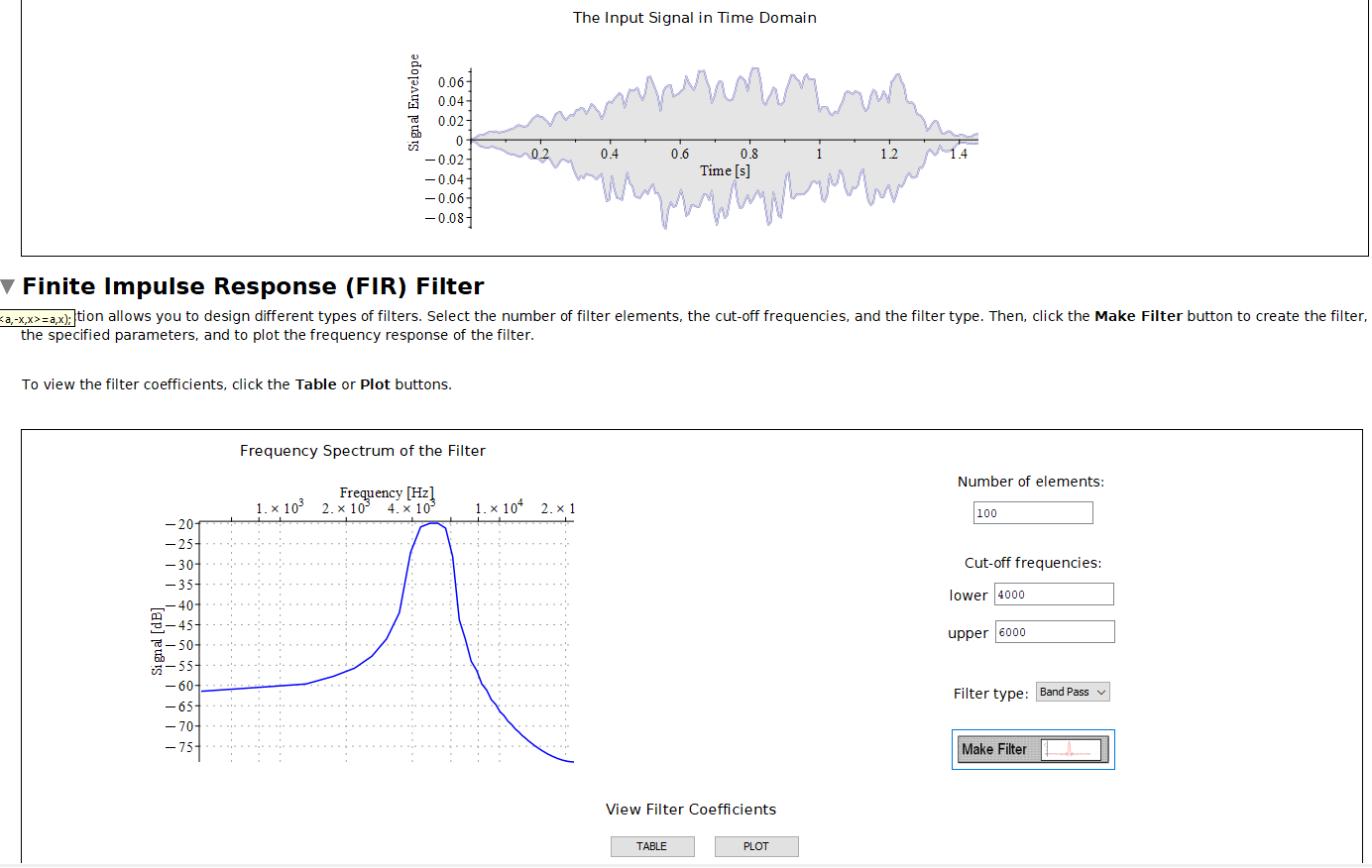
Ejemplo: diseño de filtro digitalLas transformadas de Fourier y las transformadas rápidas de Fourier pueden parecer muchas manipulaciones molestas, y puede ser difícil transmitir su importancia de una manera tangible para los estudiantes. Pero casi todos los estudiantes han escuchado audio con sonido borroso en algún momento. En este ejemplo, los estudiantes diseñan filtros de respuesta de impulso finito (FIR) para eliminar el ruido de un archivo de audio que pueden proporcionar ellos mismos. Pueden experimentar con los diferentes tipos de filtros y configuraciones sin tener que lidiar con los cálculos todavía, y ver, e incluso escuchar, por sí mismos los resultados. Al final, los estudiantes terminan con una comprensión más intuitiva de lo que significa eliminar el ruido de una señal, experimentan la necesidad de diferentes tipos de filtros para señales con diferentes características, y tienen una mejor comprensión conceptual y más motivación para aprender la matemática involucrada. |
|
Desafío 3: Superar la ansiedad matemática
Algunos estudiantes llegan a clase ansiosos y estresados incluso antes de que abras la boca. La ansiedad matemática está inhibiendo su capacidad de aprender, pero no hay suficientes horas a la semana para brindarles a estos estudiantes mucha atención adicional. Sin embargo, puede usarse la tecnología para ayudar a mejorar su confianza al:
- Ayudarles a identificar las habilidades que ya tienen
- Dándoles herramientas a las que puedan recurrir cuando se atasquen.
- Mostrándoles dónde se equivocaron y cómo solucionarlo
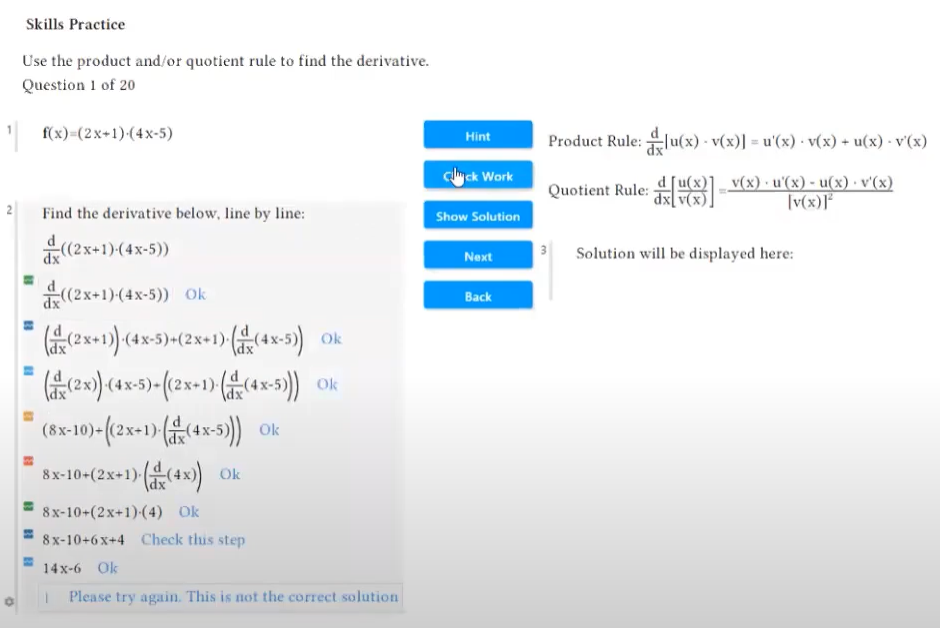
Ejemplo: Comprobación de cada línea de una solución trabajadaEl estudiante resuelve una integral en papel. Luego piden una herramienta matemática para la solución, y si son correctos, se tranquilizan y se sienten un poco menos ansiosos. Si descubre que su respuesta es incorrecta, el estudiante ansioso generalmente asume que simplemente "no lo entiende" y la ansiedad y la duda se refuerzan. Pero en lugar de detenerse allí, el estudiante puede tomar una foto de su trabajo usando una aplicación de matemáticas en su teléfono y cargar la solución completa en una herramienta en línea. Allí, pueden pedirle a la herramienta que verifique la solución completa línea por línea, y la herramienta identifica dónde cometieron el error. De esta manera, el estudiante ve dónde se equivocó y cuánto hizo correctamente. Si fue un pequeño error, se restaura su confianza en su comprensión conceptual. Si necesitan pedir ayuda, ahora tienen una pregunta más precisa, que le facilita la tarea al instructor, amigo, o otro asistente para ayudarle rápidamente, reduciendo el tiempo en el que el estudiante se siente ansioso. |
|
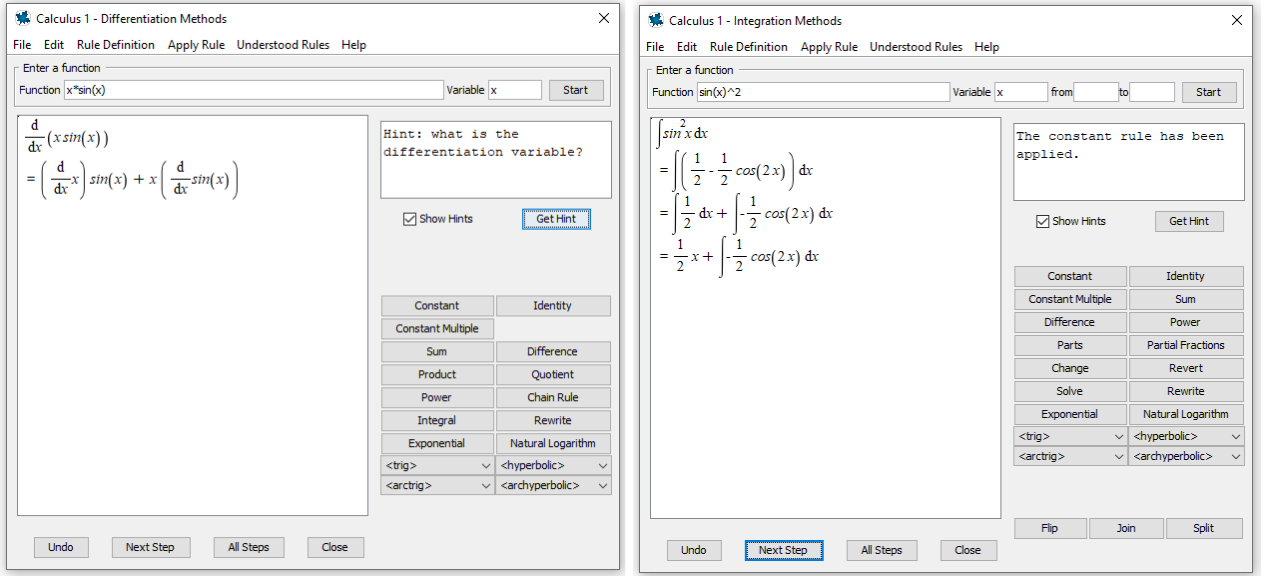
Ejemplo: Practicar la diferenciación y la integraciónEl estudiante ansioso tiende a ver cada respuesta incorrecta como una señal de que no entiende nada. Darles la oportunidad de practicar los conceptos separados de los cálculos ayuda a reforzar las ideas importantes sin la ansiedad fuera de lugar causada por errores simples. También le muestra al estudiante cuánto realmente entiende, para que pueda permanecer más tranquilo más tarde cuando desaparezca un signo menos. En este ejemplo, estas herramientas ayudan a los estudiantes a practicar las reglas de diferenciación e integración, centrándose en comprender cuándo aplicar cada método. El estudiante elige qué paso aplicar, y la herramienta realiza los cálculos reales para que el estudiante pueda concentrarse en comprender cómo resolver problemas en un nivel superior. Si tienen problemas, el tutor proporciona una pista si el estudiante comete un error, y el estudiante puede preguntar una pista o el siguiente paso, de forma que nunca se encontrará completamente estancado y desmotivado. |
|
Desafío 4: inculcar una verdadera comprensión en los estudiantes que solo están siguiendo los movimientos
Algunos estudiantes pueden imitar lo que aprenden en clase, pero no tienen una comprensión real de lo que están haciendo y por qué. Trabajan a través de los pasos y llegan a una respuesta, pero solo están siguiendo los movimientos. Si cambia ligeramente el tipo de problema, no se darán cuenta o no sabrán qué hacer. Desea que sus alumnos entiendan realmente lo que están haciendo, no que apliquen ciegamente un algoritmo.
En muchos casos, una buena manera de lograr el objetivo de comprensión es ayudar a los estudiantes a visualizar los conceptos detrás de los pasos, y la tecnología puede ayudarlo a hacerlo.
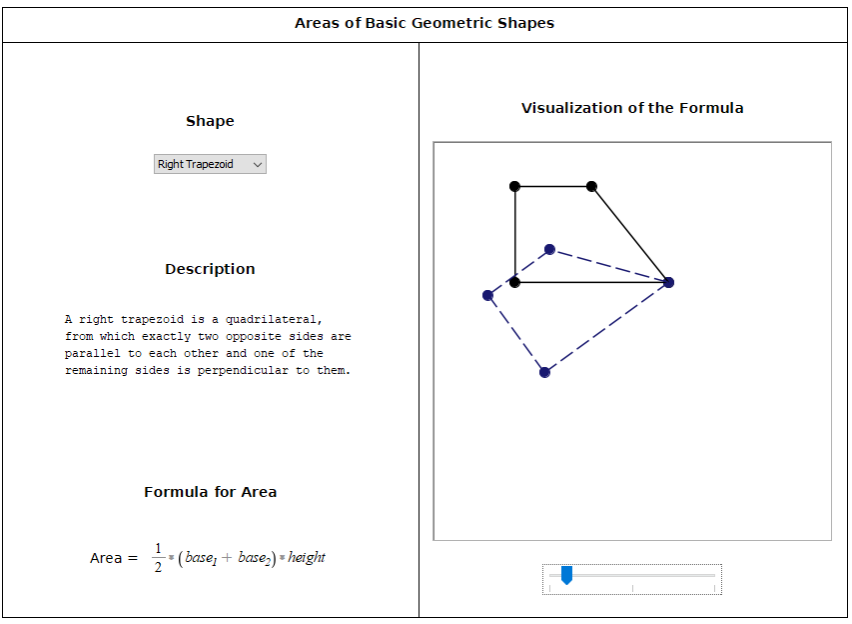
Ejemplo: fórmulas de área de formas geométricas básicasEn esta aplicación, los estudiantes pueden animar la construcción geométrica detrás de la fórmula del área de una forma determinada. Ahora, en lugar de memorizar un montón de fórmulas aparentemente aleatorias, pueden ver de dónde provienen esas fórmulas, lo que les ayudará a recordarlas y también les proporcionará técnicas para abordar problemas más avanzados. Ver: Comprensión de las fórmulas de área de formas geométricas |
|
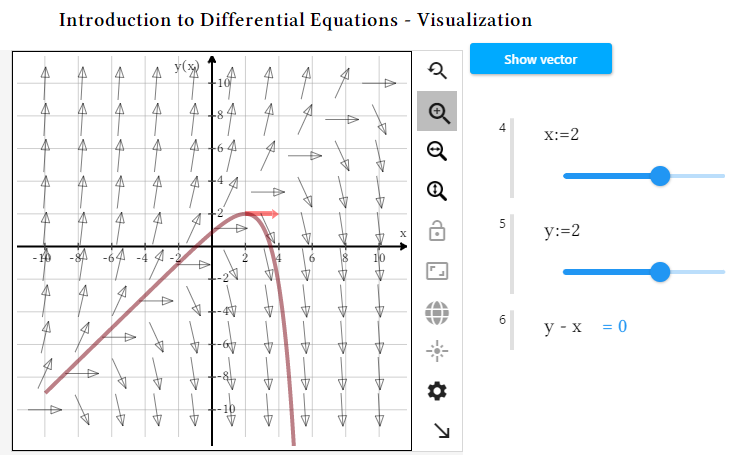
Ejemplo: comprensión de ecuaciones diferencialesUna cosa es seguir los pasos para resolver una ecuación diferencial, pero otra muy distinta es "captar" lo que realmente está pasando y por qué hay soluciones generales y soluciones particulares. En este ejemplo, los estudiantes ven un campo de dirección para la ecuación diferencial elegida, la flecha de dirección en un punto específico y cómo la traza de una solución aproximada a través de ese punto sigue las flechas. Pueden experimentar seleccionando diferentes puntos y viendo cómo el vector y la solución cambian cada vez. Desarrollar su comprensión intuitiva a través de este tipo de exploración brinda a los estudiantes una base sólida sobre la cual desarrollar más habilidades. |
|
Desafío 5: Proporcionar suficientes oportunidades para la práctica
Las visualizaciones que promueven la comprensión conceptual son importantes, pero también necesita que sus alumnos se arremanguen y comiencen a resolver problemas. muchos problemas Pero hay tantos problemas con soluciones en el libro de texto, y muy a menudo, eso no será suficiente práctica para algunos estudiantes.
Con la tecnología adecuada, los estudiantes tienen acceso a un conjunto inagotable de problemas de práctica que les permite practicar todo lo que necesitan. La herramienta les dirá a los estudiantes si están en lo correcto o no, para que puedan generar confianza a medida que desarrollan sus habilidades. Aún mejor, algunas herramientas pueden incluso ayudar a los estudiantes a comprender dónde se equivocaron y cómo volver a encarrilarse.
Ejemplo: Práctica para hallar derivadas: Reglas del producto y del cocienteEn este ejemplo, la herramienta genera una secuencia de problemas de práctica que están diseñados para que los estudiantes practiquen con un conjunto muy específico de habilidades: aplicar las reglas del producto y el cociente para encontrar derivadas. El estudiante primero resuelve el problema en papel, luego usa una aplicación de matemáticas en su teléfono para tomar una foto y cargarla en la herramienta, y hace clic en Verificar trabajo. La herramienta examina cada línea de su solución y, en este caso, le dice al estudiante que cometió un error en el penúltimo paso. El estudiante entonces ve que aplicó las reglas correctamente pero cometió un error aritmético en su derivación. Corrigen el error en el documento, lo revisan nuevamente y luego pasan al siguiente problema. El estudiante también puede pedir pistas, y debido a que el instructor decide permitirlo, pueden solicitar ver la solución completa cuando necesiten otro ejemplo que les ayude a entender. Ver: Práctica: Hallar derivadas usando las reglas del producto y del cociente |
|
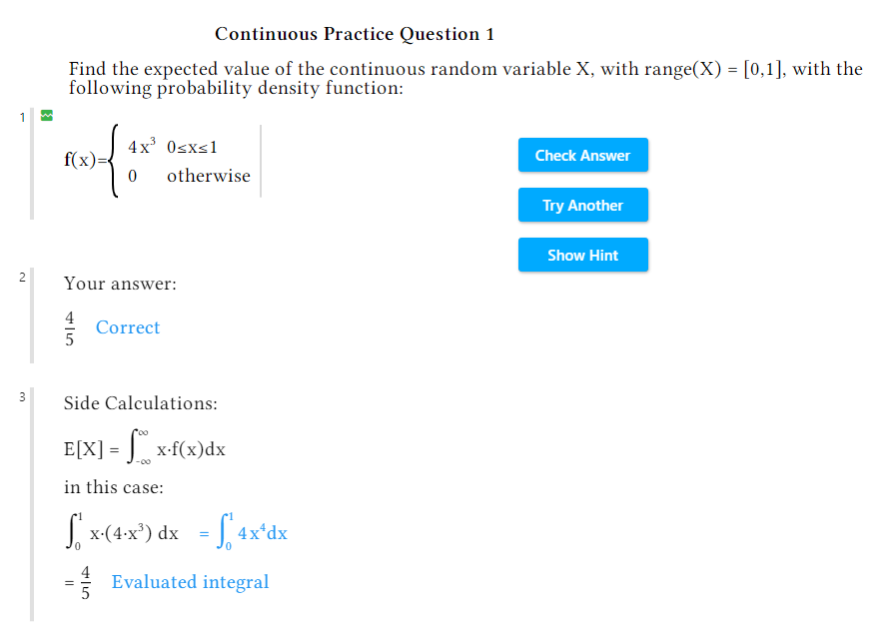
Ejemplo: valor esperadoEste documento genera preguntas que permiten a los estudiantes practicar cómo encontrar el valor esperado de una variable aleatoria continua y luego verificar sus respuestas. Los estudiantes primero resuelven la solución dentro del propio documento, utilizando una combinación de pasos manuales y cálculos realizados por la herramienta. En este caso, el instructor optó por no incluir la opción de ver las soluciones completas, pero permitió sugerencias. |
|
Desafío 6: Evaluar el progreso en un mundo donde es fácil buscar respuestas
En estos días, su estudiante puede obtener respuestas a las preguntas estándar del tipo "Resolver esto" fácilmente, ya sea que entiendan lo que están haciendo o no. Puede tener una idea mucho mejor del aprendizaje de sus alumnos al asignarles tareas y proyectos que se centren en resolver problemas conceptuales. A menudo, estos proyectos implicarán una combinación de pruebas de hipótesis, visualización, explicaciones escritas, cálculos que desea que hagan ellos mismos y cálculos por los que no desea que tengan que preocuparse. La plataforma tecnológica adecuada puede proporcionarle el entorno que necesita para configurar proyectos interesantes que su alumno no puede realizar simplemente buscando respuestas. En cambio, necesitan pensar, cuestionar, comunicarse y aprender.
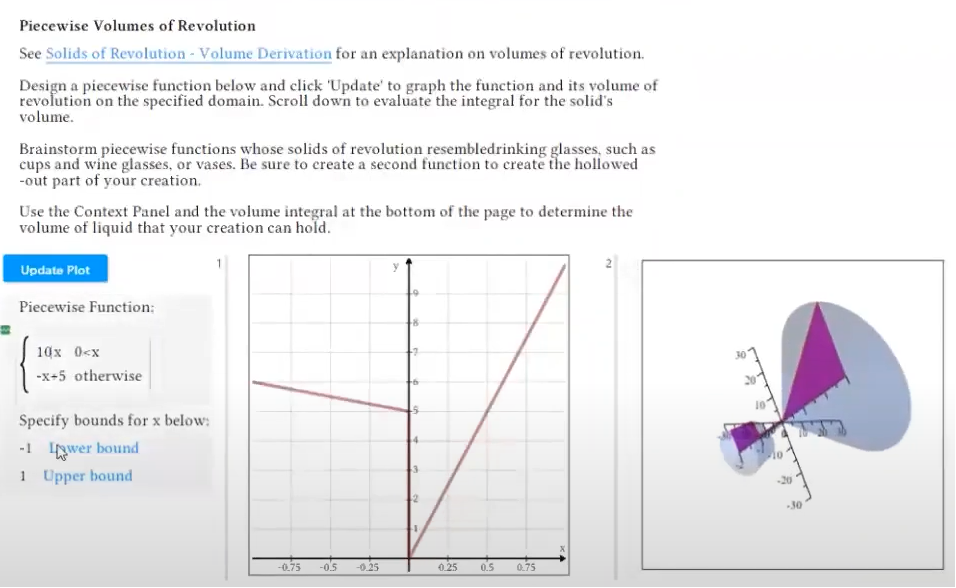
Ejemplo: sólidos de revoluciónEn este proyecto, se desafía a los estudiantes a idear una función por partes cuyo sólido de revolución parezca una copa de vino o un jarrón. Los estudiantes pueden probar varias funciones, con varios límites superior e inferior, y ver los resultados. Muy rápidamente comienzan a pensar en cómo necesitarían cambiar la función para obtener una forma más deseable. El instructor también puede establecer un requisito para el volumen mínimo o máximo del recipiente, y los estudiantes pueden usar el software para configurar y resolver la integral para determinar el volumen de cada forma y luego hacer más ajustes a su función para refinar su vaso. o florero. Todavía en el mismo entorno, el instructor puede pedir a los estudiantes que respondan preguntas que requieran que comuniquen sus reflexiones y procesos de pensamiento. Ver: Proyecto: Diseñe una copa de vino con sólidos de revolución |
|
Desafío 7: Manejar diferentes niveles de preparación para el curso
Los estudiantes ingresan a su clase con diferentes antecedentes y diferentes niveles de preparación. Quiere ayudar a los estudiantes menos preparados a alcanzar a sus compañeros y tener éxito, pero no hay tiempo para brindar ayuda individual a todos esos estudiantes. Y eso es incluso antes de pensar en los estudiantes más avanzados, a quienes le gustaría mantener desafiados y fomentar sus habilidades e interés en el tema. Pero un buen repositorio de contenido interactivo listo para usar, que cubre diferentes temas y niveles, significa que los estudiantes con diferentes necesidades tienen acceso a materiales que los ayudarán a aprender por sí mismos. Y cuando ese contenido se puede personalizar fácilmente, puede usarlo como punto de partida para desarrollar recursos dirigidos con mayor precisión, para el autoaprendizaje, demostraciones en el aula, proyectos o lo que necesite.
Ejemplo: recursos de contenidoEl contenido y las herramientas para ayudar a los estudiantes a usar las soluciones de Maplesoft Mathematics Suite incluyen:
|
|
- Detalles
- Categoría: Comsol
- Visto: 4331
Nueva página sectorial de COMSOL dedicada a la innovación en la industria farmacéutica a partir de la simulación
La incorporación de la simulación multifísica de COMSOL Multiphysics® en el trabajo de I+D de científicos e ingenieros del sector farmacéutico ayuda y agiliza el proceso de crear nuevos y mejores productos y tratamientos al tiempo que reduce los costes y la necesidad de pruebas in vitro e in vivo.
Visite la página a través del enlace inferior
- Detalles
- Categoría: Minitab
- Visto: 4214
Por Cody Steele.
En esta era moderna, algunos de nosotros tenemos la suerte de contar con un proceso que permite una inspección económica, instantánea y no destructiva del 100% de lo que fabricamos. Para todos los demás, el análisis de capacidad es extremadamente útil. Si se considera, por ejemplo, la elaboración del vino: las medidas son más difíciles. En cuanto se añade peróxido de hidrógeno a una muestra de vino para comenzar a medir sus características químicas, ésta ya no se vuelve a poner en una botella para venderla. Obtener la información que se necesita rápidamente y a partir de la menor cantidad de muestras posible marcará una gran diferencia.
Se utiliza el análisis de capacidad para evaluar qué tan bien se está desempeñando un proceso con respecto a los límites de especificación. A primera vista, si las medidas que se tienen están dentro de las especificaciones, entonces se piensa que el proceso está funcionando bien. El análisis de capacidad va más allá de este enfoque simple y binario para proporcionar información sobre lo bien que un proceso cumple con las especificaciones. Considerense los histogramas siguientes que muestran mediciones de valores de pH. En el producto terminado, los valores deben estar dentro de los límites de especificación de 3.3 y 3.7.
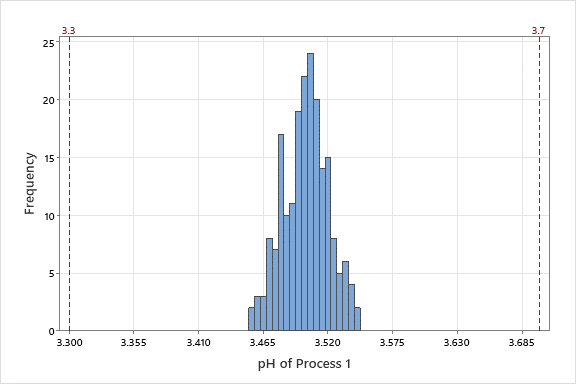
En el Proceso 1, existe una amplia brecha entre las mediciones y los límites de especificación.
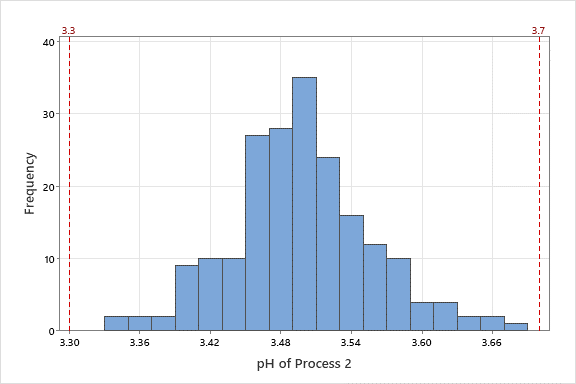
En el Proceso 2, las medidas se acercan a los límites de especificación. En ambos procesos, todas las medidas están dentro de los límites de especificación. Debido a que los histogramas muestran una muestra del proceso, estaríamos mucho más preocupados de que el Proceso 2 pudiera tener mediciones fuera de los límites de especificación. El análisis de capacidad distingue algo como el Proceso 1 del Proceso 2 para que sepamos dónde son más valiosos nuestros esfuerzos de mejora.
DOS MEDIDAS COMUNES DE CAPACIDAD
Muchas medidas diferentes de capacidad están en uso. Dos de los más fáciles de entender son Pp y Ppk.
¿Qué es Pp?
Pp es una relación que compara la distancia entre los límites de especificación con el rango estimado del proceso.
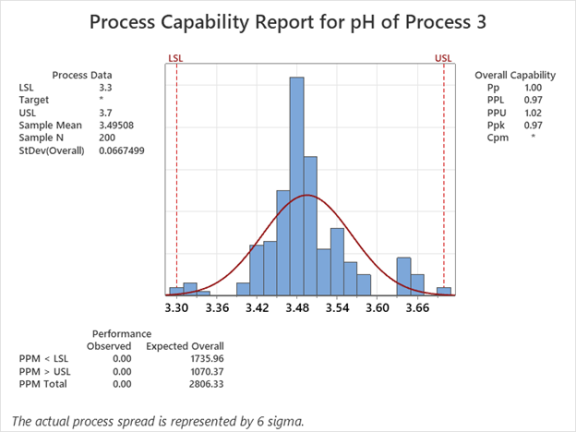
Cuando el rango estimado es igual a la distancia entre los límites de especificación, entonces Pp es 1.
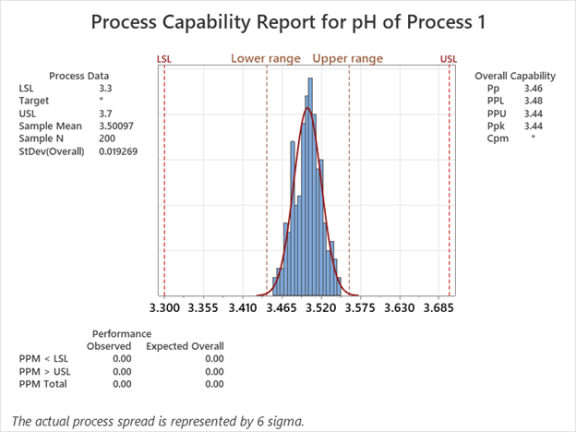
Cuanto más estrecho es el rango estimado, mejor se comporta el proceso, lo que da valores más altos de Pp. Aunque los diferentes productos y procesos tienen diferentes estándares, a menudo verá 1.33 como una meta para Pp.
¿Qué es Ppk?
Cuando un proceso no está centrado, Ppk es una mejor representación de la capacidad de los procesos para proporcionar productos que cumplen con las especificaciones de los clientes. En lugar de la distancia entre los límites de especificación, Ppk usa la distancia desde el promedio de las mediciones hasta el límite de especificación más cercano. En lugar del rango de proceso estimado, Ppk usa la mitad del rango de proceso estimado. El resultado es una medida que considera dónde está el promedio del proceso en relación con los límites de especificación.
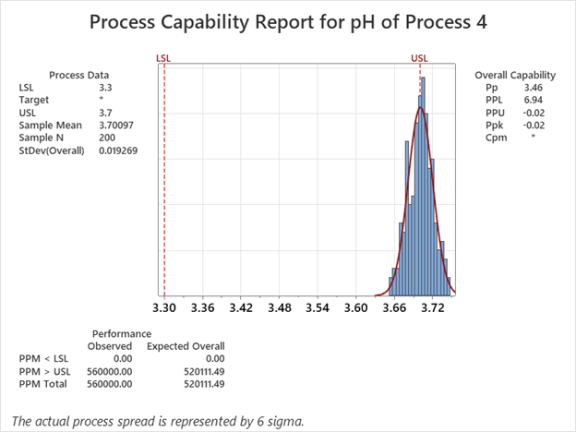
Por ejemplo, el valor de Pp de 3,46 indica que el proceso funciona bien aunque más de la mitad de las mediciones están fuera del límite de especificación. El valor Ppk de -0,02 indica que el proceso funciona mal. Debido a que el proceso funciona mal, Ppk es la mejor medida para ver que el proceso necesita mejoras.
Por qué se necesita un análisis de capacidad
Cuando se toman decisiones sobre la mejora de procesos, a menudo no es suficiente saber si una muestra de productos está dentro de los límites de especificación. Se necesita una forma más detallada de describir qué tan efectivo es un proceso para cumplir con las especificaciones del cliente. Si se necesita saber dónde enfocar los esfuerzos de mejora, entonces se necesita un análisis de capacidad.