- Detalles
- Categoría: Minitab
- Visto: 10301
Minitab informa a los usuarios que disponen de una licencia de su software estadístico Minitab 17, en el caso de que no hayan actualizado a Minitab 18, que la política de soporte de Minitab actual indica que una versión del software solo está soportada durante un año después de que la próxima versión es liberada. Como Minitab 18 fue liberada en junio de 2017, el soporte para Minitab 17 finalizará el próximo 7 de junio de 2018.
Soporte limitado para Minitab 17 a partir del 8 de junio de 2018:
- Asistencia sobre el uso del software o interpretación de los resultados - se discontinua el servicio después del 7 de junio de 2018.
- Soporte al licenciamiento – se incluye asistencia para el paso de la licencia a un nuevo PC.
Por favor, nótese que Minitab actualmente proporciona Soporte de licenciamiento limitado para Minitab 16, pero este servicio dejará de proporcionarse después del 7 de junio de 2018, ya que este producto habrá alcanzado su final de vida útil.
Minitab 18 lleva nuevas y mejoradas funcionalidades estadísticas – incluyendo una ventana de sesión actualizada, la capacidad de ordenar hojas de trabajo, diseños definitivos de criba y más distribuciones para intervalos de tolerancia.
- Detalles
- Categoría: Minitab
- Visto: 7345
Minitab informa que su política de Soporte actual indica que una versión de su software Companion by Minitab (antes conocido como Quality Companion) dispone de soporte completo hasta un año después de la liberación de la siguiente versión. Como Companion by Minitab fue liberado en primavera de 2017, el soporte completo para Quality Companion 3 finalizará el 7 de junio de 2018.
Companion by Minitab es una aplicación diseñada específicamente para ejecutar y reportar proyectos de mejora continua. Incluye herramientas como FMEA, mapas de flujo devalor, y simulación de Monte Carlo con un panel de configuración (dashboard) que proporciona resúmenes de un programa completo de mejora de la compañía.
- Detalles
- Categoría: Twinn Witness
- Visto: 10465
El departamento de Sistemas y Automatización de Fabricación de la Universidad Técnica de Liberec, en la República Checa, aboga desde hace mucho tiempo por la tecnología de simulación predictiva de Lanner, WITNESS, que utiliza tanto en sus enseñanzas académicas como en sus colaboraciones con socios fabricantes.
La Universidad Técnica de Liberec y WITNESS
El uso de la simulación predictiva es versátil, añade gran valor a muchas industrias y aplicaciones, desde el diseño o el análisis de una línea de producción a la planificación de mantenimiento o la justificación de opciones de negocio. Gracias a su versatilidad es, naturalmente, una parte crucial del currículum académico para aquellos que estudian un grado enfocado a la fabricación.
La Simulación Predictiva es un tema principal enseñado en el Departamento de Sistemas y Automatización de Fabricación de la Universidad Técnica de Liberec, que trabaja estrechamente con varios socios fabricantes. El Departamento tiene licencias, tanto académicas como para uso en consultoría, proporcionando a los estudiantes la oportunidad de sumergirse tanto en proyectos teóricos como del mundo real.
¿Cómo se utiliza la simulación para la enseñanza?
El lema “Innovar o Morir” no escapa a la educación superior. Las difíciles condiciones del mercado requieren que el sector educacional responda y permanezca al frente de la última tecnología, proporcionando a sus estudiantes un conjunto completo de competencias que les permitirá añadir valor en cuanto empiecen a trabajar. Para enseñar estos últimos conceptos y proporcionar a los estudiantes estas capacidades que necesitan, las universidades se han volcado en la simulación.
En las Universidades Técnicas, el software de simulación predictiva de Lanner, WITNESS, es utilizado para demostrar estos conceptos y enseñar a los alumnos cómo acercarse a las demandas comunes de los fabricantes. A través del curso de sus estudios, a los estudiantes se les enseña:
- los principios básicos de un proceso de fabricación
- los diferentes métodos que se pueden aplicar a un proceso de fabricación
- cómo diseñar un modelo de simulación
- cómo diseñar un juego de simulación
- cómo el modelado de simulación forma parte de un proyecto integral
Enseñanza de los principios básicos de un proceso de fabricación
Para introducir a los estudiantes en la simulación y WITNESS, las universidades técnicas empiezan con los modelos más simples que ayudan a explicar los principios básicos y los pasos dentro de un proceso de fabricación. Con el uso de un modelo de demostración predefinido a los alumnos se les enseña:
- los parámetros estocásticos que afectan a la producción
- cómo un proceso de fabricación es depende de todas las operaciones en funcionamiento
- cómo los canales de distribución pueden impactar en la producción
- las ventajas y desventajas de la agrupación de recursos y la reorganización de la mano de obra
- asuntos que surgen por los cuellos de botella en los procesos de producción
- la diferencia entre los controles empuje y atracción
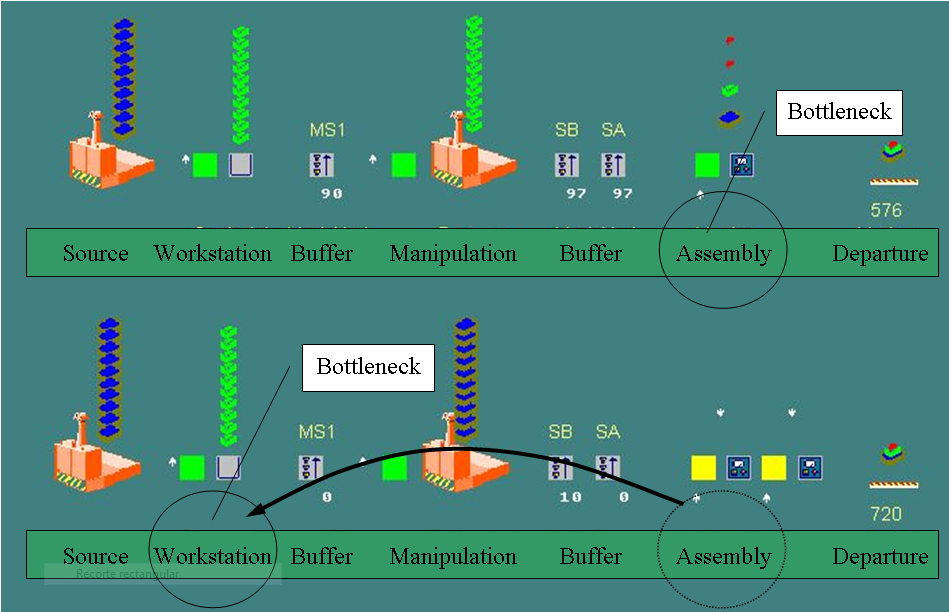
Como ejemplo, el modelo mostrado en la figura 1 ayuda a explicar la Teoría de Restricciones (TOC, o Theory of Constrains) y los asuntos que pueden surgir cuando existen cuellos de botella dentro de los procesos de producción. En este primer ejemplo, los cuellos de botella se forman en la línea de ensamblaje. Se ponen a disposición recursos adicionales para eliminar el cuello de botella, sin embargo esto entonces causa otro cuello de botella relentizando el proceso de producción, en la Estación de trabajo.
Fig. 1. Problema de desplazamiento del cuello de botella
Metodología para influir en un proceso de fabricación
Una vez que se han enseñado los conceptos básicos de un proceso de fabricación, otro conjunto de modelos docentes de simulación con WITNESS son utilizados para demostrar diferentes métodos de diseño e influencia sobre los procesos de fabricación. A través del estrecho trabajo realizado entre la Universidad Técnica y sus socios fabricantes, existe un rico conjunto de experiencias del mundo real de las que los estudiantes pueden partir. Se discuten las ventajas y desventajas de varias metodologías. Estas incluyen:
- Estrategia Just in Time (JIT) – donde la demanda debe de predecirse con precisión para asegurar que solo el stock requerido está disponible
- Metodología Kanban – descubrimiento de los problemas del proceso para crear una producción más consistente y una fuerza de trabajo colaborativa
- Sistema de fabricación flexible: Flexible Manufacturing System (FMS) – donde los procesos reaccionan a los cambios, creando una línea de producción más eficiente
- Fabricación celular – donde la producción de varios productos similares se mueve a un ritmo acelerado para obtener eficiencia y pocos desperdicios
- Línea de producción en U – donde el comienzo y el final de la línea de producción están cerca uno del otro lo que permite una colaboración más fácil entre las diferentes operaciones a lo largo de la línea
Diseñar un modelo de simulación
Una parte integral del proceso de aprendizaje es cuando los estudiantes empiezan a construir e interactuar con sus propios modelos de WITNESS. Aprender a analizar un problema dado y diseñar soluciones apropiadas, mientras se dominan los principios básicos de la simulación, son requisitos fundamentales para los estudiantes.
Durante el semestre, a los estudiantes se les asigna una tarea para crear una línea de producción de fabricación. Para alcanzar los objetivos deben determiner el tamaño de la línea de producción, el número apropiado de puestos de trabajo, operadores y personal, y preparar un modelo de simulación sencillo que alcance los objetivos del cliente. Al mismo tiempo, los alumnos deben de intentar mantener los costes bajos.
El papel de los juegos de simulación
En las Universidades Técnicas, la simulación también se utiliza en un área no tradicional, con la creación de un juego de simulación, que se combina con vídeos para obtener una representación realista del proceso.
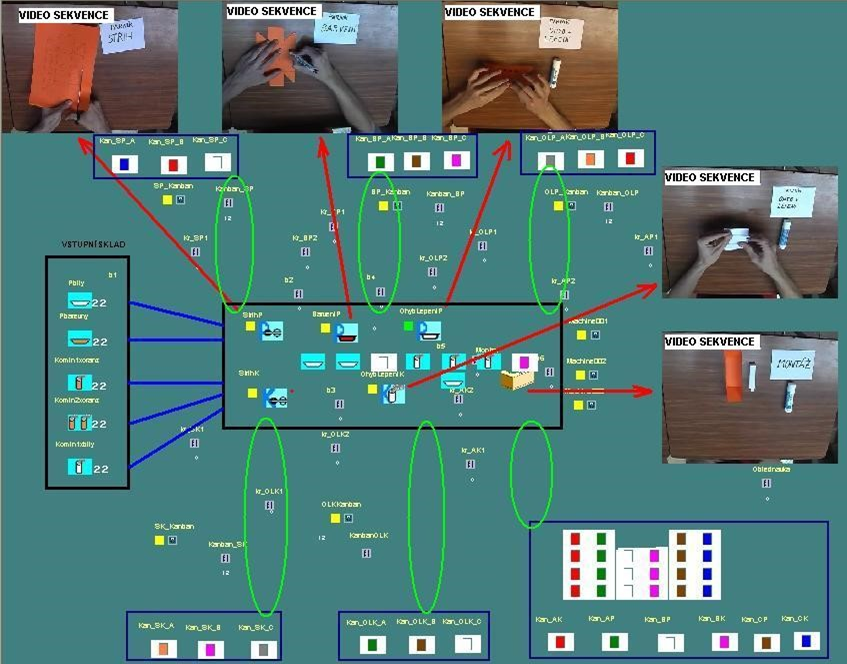
Utilizando el juego como método de aprendizaje, los estudiantes son introducidos en un proceso específico y las cortas secuencias de video construidas en el modelo ilustran mejor el punto. Diferentes escenarios posibilitan practicar la responsividad y el pensamiento creativo, preparando a los estudiantes para eventos inesperados en un entorno del mundo real. El siguiente gráfico muestra el juego de simulación "Production of KVS steamers" en el que WITNESS es utilizado para presentar el proceso de producción por un lado y el sistema Kanban por otro.
Fig. 2. Juego de simulación en el entorno WITNESS
Demostrar el uso de la simulación
El sistema educativo en la Universidad Técnica complementa la enseñanza “tradicional” de temas especializados en el campo de la fabricación y lo enriquece significativamente. A los estudiantes en el sistema de la Universidad Técnica se les pide que formen parte de un proyecto integral donde deben de diseñar y construir una línea de producción completa desde el principio hasta el final, para demostrar su comprensión de lo que se les ha enseñado.
Deben de diseñar un prototipo en CAD, crear la disposición del taller, programar la producción de piezas utilizando el sistema de información de gestión de la empresa, fabricar físicamente el producto en las máquinas CNC, y verificar la precisión de la producción. Los estudiantes trabajan en equipo durante este proyecto.
La simulación WITNESS se utiliza para examinar los diseños y soluciones propuestas, asegurando que el diseño de la línea de producción puede ajustarse a las demandas del proceso establecido.
Este proyecto reúne todo lo que se ha enseñado a los alumnos, y asegura que entienden cómo aplicar la simulación y el valor que puede aportar a cualquier proceso de fabricación.
El valor de la simulación en educación
La simulación predictiva es una competencia crucial a enseñar a los estudiantes de hoy. La experiencia teórica y práctica que obtienen durante sus estudios, les prepara para convertirse en valiosos activos para cualquier empresa a la que se incorporen tras la graduación. Como estudiantes, los que continúan sus estudios en la Universidad Técnica con maestrías y las tesis doctorales, la aplicación de la simulación y sus posibilidades son exploradas en mayor profundidad.
En un mundo siempre cambiante, donde la necesidad de procesos eficientes es crítica para asegurar el provecho y el éxito, las universidades deben de asegurar a sus alumnos que están entrando en el mundo laboral con las herramientas para tener éxito.
- Detalles
- Categoría: Minitab
- Visto: 156571
Por Eston Martz
La gente puede cometer errores cuando realiza un test de hipótesis con análisis estadísticos. Específicamente, pueden hacer errores de Tipo I o Tipo II.
A medida que se analizan los propios datos y se hacen test de las hipótesis, la comprensión de la diferencia entre los errores de Tipo I y Tipo II se convierte en algo extremadamente importante, porque existe un riesgo de cometer cada tipo de error en cada análisis, y la cantidad del riesgo está bajo nuestro control.
Así que si se está testeando una hipótesis sobre un asunto de seguridad o calidad que podría afectar a la vida de las personas, o un proyecto que podría ahorrar millones de dólares a su negocio, ¿qué tipo de error tendría consecuencias más serias o más costosas? ¿Existe un tipo de error que sea más importante de controlar que otro?
Antes de que intentemos contestar a esta pregunta, revisemos qué son estos errores.
La hipótesis nula y los errores de Tipo I y 2
Cuando los estadísticos se refieren a errores de Tipo I y Tipo II, nos referimos a las dos maneras en que se pueden realizar errores respecto a la hipótesis nula (Ho). La hipótesis nula es la posición por defecto, semejante a la idea de “inocencia hasta que se pruebe la culpabilidad”. Cualquier test de hipótesis se empieza con la asunción de que la hipótesis nula es correcta.
Cometemos un error de Tipo I si rechazamos la hipótesis nula cuando ésta es cierta. Se trata de un falso positivo, como una alarma de fuego que suena cuando no existe tal fuego.
Un error de Tipo II ocurre si nos equivocamos al rechazar el nulo cuando no es cierto. Es el caso de un falso negativo—como una alarma que falla y no suena cuando existe un fuego.
Es más fácil de comprenderlo en la tabla siguiente, semejante a la que se puede encontrar en cada texto sobre estadística:
| Realidad | Hipótesis nula (H0) no rechazada | Hipótesis nula (H0) rechazada |
| H0 es cierta. | Conclusión correcta. | Error Tipo I |
| H0 es falsa. | Error Tipo II | Conclusión correcta. |
Estos errores están relacionados con los conceptos estadísticos de riesgo, significancia y potencia.
Reducir el riesgo de errores estadísticos
Los estadísticos llaman al riesgo, o probabilidad, de cometer un error de Tipo I “alfa,” igual que el “nivel de significación”. En otras palabras, es la voluntad de arriesgarse rechazando la hipótesis nula cuando es cierta. Alfa normalmente se pone a 0.05, que es una posibilidad del 5 por ciento de rechazar la hipótesis nula cuando es cierta. Cuanto más pequeña sea alfa, menor es el riesgo de rechazar la hipótesis nula incorrectamente. En situaciones de vida o muerte, por ejemplo, una alfa de 0.01 reduce la probabilidad de un error Tipo I a justo un 1 por ciento.
Un error de Tipo II está relacionado con el concepto de “potencia”, y la probabilidad de cometer este error se refiere como “beta”. Podemos reducir nuestro riesgo de cometer un error Tipo II asegurando que nuestro test tiene suficiente potencia—lo que depende de si el tamaño de la muestra es suficientemente grande para detectar una diferencia cuando ésta existe.
El argumento por defecto para "Qué error es peor"
Volvamos a la cuestión de qué error, Tipo I o Tipo II, es peor. El ejemplo de referencia para ayudar a la gente a pensar sobre el tema es un acusado de un crimen que exige una sentencia muy dura.
La hipótesis nula es que el acusado es inocente. Por supuesto no se querrá librar a una persona culpable de la cárcel, pero la mayoría de la gente diría que sentenciar a una persona inocente a esa pena es una consecuencia todavía peor.
Por lo tanto, muchos textos e instructores dirán que el Tipo I (falso positivo) es peor que un error Tipo II (falso negativo). La razón se reduce a la idea que si se mantiene el status quo o asunción por defecto, al menos no se estará haciendo las cosas peor.
Y en muchos casos, eso es cierto. Pero como pasa tanto en estadística, en la aplicación nada es realmente tan blanco o negro. La analogía del acusado es muy Buena para enseñar el concepto, pero cuando se intenta hacer una regla de oro sobre qué tipo de error es peor en la práctica, se desmorona.
Pero entonces, ¿qué tipo de error es el peor?
Siento decepcionar, pero como en tantas cosas de la vida y la estadística, la respuesta más honesta a esta pregunta tiene que ser, “depende”.
En alguna situación, el error de Tipo I puede tener consecuencias menos aceptables que las que tendría un error de Tipo II. En otras, el error Tipo II podría ser menos costosos que un error Tipo I. Y, a veces, como Dan Smith indicó en Significance hace unos años, respecto a Seis Sigma y mejora de calidad, "ninguno" es la única respuesta a qué error es el peor:
La mayoría de estudiantes de Seis Sigma van a utilizar los conceptos que aprenden en el contexto de los negocios. En las empresas, cuando le cuestas a la compañía 3 millones de dólares por sugerirle un proceso alternativo cuando no hay nada de malo con el proceso actual o dejas de tener en cuenta 3 millones de dólares de ganancias cuando deberías cambiar a un nuevo proceso pero te equivocas, el resultado final es el mismo. La empresa pierde la posibilidad de obtener un beneficio adicional de 3 millones de dólares.
Mira a las potenciales consecuencias
Como no existe una regla de oro clara sobre qué tipos de errores, Tipo I o Tipo II, son peores, nuestra mejor opción al utilizar datos para verificar una hipótesis es mirar cuidadosamente a las consecuencias que podrían seguir a ambos tipos de errores. Varios expertos sugieren utilizar una tabla como la siguiente para detallar las consecuencias para un error del Tipo I y del Tipo II, en el análisis particular.
| Nula | Error tipo I: H0 verdadero, pero rechazado | Error tipo II: H0 falso, pero no rechazado |
| Medicina A no alivia la Condición B. | Medicina A no alivia la Condición B, pero no se elimina como opción de tratamiento. | Medicina A alivia la Condición B, pero es eliminada como opción de tratamiento. |
| Consecuencias | Los pacientes con Condición B, que reciben la medicina A no se alivian. Pueden experimentar empeoramiento y/o efectos secundarios hasta incluso morir. Posible litigio. | Un tratamiento viable permanece inaccesible a pacientes con Condición B. Se pierden los costes del desarrollo. Provecho potencial eliminado. |
Sea lo que sea lo que involucre el análisis, comprender la diferencia entre los errores de Tipo I y Tipo II, y considerar y mitigar sus respectivos riesgos como apropiados, siempre es inteligente. Para cada tipo de error, hay que asegurarse de que se responde esta pregunta: "¿Qué es lo peor que puede ocurrir?"
Para explorar este tema más extensamente, compruebe este artículo sobre el uso de cálculo de potencia y tamaño de la muestra para equilibrar el riesgo de un error de tipo II y los costes de la comprobación, o esta entrada del blog sobre considerar el alfa apropiado para su test particular.
- Detalles
- Categoría: Comsol
- Visto: 5491
Los próximos días 18 a 20 de octubre tendrá lugar en Rotterdam la Conferencia de COMSOL 2017. Asista a este interesante evento para avanzar en sus conocimientos de simulación numérica y contactar con los mejores expertos en diseño y modelado. El evento de este año se enfoca en la divulgación de las ventajas de la simulación a través del análisis multifísico y las apps de simulación especializadas. Miles de asistentes de todo el mundo compartirán sus experiencias con el modelado y la construcción de apps. Únase a nosotros en la Conferencia de COMSOL para:
|
- Detalles
- Categoría: Lakes
- Visto: 6119
AERMOD View Versión 9.5 ya está disponible. Esta versión contiene las siguientes implementaciones:
- Informe de receptor sensible: Los receptores discretos pueden marcarse como “Sensibles”, apareciendo sus resultados en un completamente nuevo Informe de Resumen.
- Mapas de losetas actualizado: El servidor de mapas cíclico abierto se ha actualizado con la última información del servidor y el hospedaje.
- Opciones gráficas: La funcionalidad de disposiciones actualizada permite una rápida aplicación de los ajustes de contornos para archivos de gráficos múltiples de una vez.
- Copia de respaldo del proyecto: La opción de copia de respaldo del proyecto de AERMOD View ahora incluye todos los archivos asociados con las ejecuciones realizadas utilizando la utilidad Multi-Chemical.
- Temas adicionales: Vea las notas de la versión completas para una lista detallada de todos los cambios
- Detalles
- Categoría: Comsol
- Visto: 6178
Por Jose Miguel Campillo-Robles, Xabier Artetxe, y Karmele del Teso Sánchez de la Universidad de Mondragón
Applied Physics Letters.
Uno de los principios básicos para obtener altas intensidades en una celda de almacenamiento de energía electroquímica es minimizar la resistencia interna. La resistencia generada por los colectores de corriente, no ha recibido suficiente atención en el pasado, posiblemente porque no se consideró importante en baterías y supercondensadores de baja potencia. Sin embargo, el desarrollo de celdas de alta potencia ha reducido otras fuentes de resistencia interna, y la caída potencial de los colectores se ha vuelto más importante. Además, la miniaturización de los dispositivos de almacenamiento de energía aumenta las pérdidas óhmicas en los colectores de corriente, debido a la reducción del tamaño. En este trabajo, hemos desarrollado un modelo eléctrico para evaluar el efecto del espesor del colector de corriente en la caída de potencial máximo.
La información obtenida de estas simulaciones es extremadamente útil para el prototipado, diseño y optimización de celdas de almacenamiento de energía electroquímica (baterías de ion litio, supercondensadores, etc.). Hemos demostrado que el grosor de los colectores de corriente es un parámetro crítico para el diseño de las celdas. Reduciendo el espesor de estos colectores de corriente, podemos obtener diferentes beneficios: mayor densidad de energía, mayor potencia energética y menor gasto en materiales. Sin embargo, como resultado, la resistencia interna de los colectores de corriente aumenta, y puede darse un calentamiento peligroso. Además, también podrían producirse deformaciones mecánicas de los colectores de corriente. Es evidente, que es necesario lograr un equilibrio entre todos los parámetros del diseño de la celda.