- Detalles
- Categoría: Comsol
- Visto: 8149
Por Brianne Costa
En cuanto sales a trabajar, la puerta del garaje se cierra y escribes a la cafetera de la oficina para que empiece a preparar un café recién hecho. Durante el día tu sistema de aspersión obtiene un informe de que va a llover y cancela el riego de la tarde. No se trata de un programa futurista de la televisión, es Internet de las Cosas, y con 5G, la próxima generación de comunicaciones inalámbricas, está a punto de llegar. Primero necesitamos optimizar el rendimiento de las antenas de los dispositivos móviles existentes.
La próxima generación de tecnología móvil: Internet de las Cosas y 5G
Una serie de consumidores expertos en tecnología ya han configurado sus hogares con algún grado de automatización, como utilizar apps en sus móviles para arrancar el lavavajillas o ajustar sus termostatos. Un fenómeno relativamente nuevo, el Internet de las Cosas (en inglés Internet of Things o IoT), también llamado "Internet Industrial" o incluso "Intenet de Todo", lleva estas simples tareas automatizadas al siguiente nivel permitiendo que los objetos comuniquen sus datos con otros dispositivos conectados.

En definitiva, IoT como lo conocemos progresará de sencillas automatismos en casa y en los edificios a áreas de aplicación mucho más avanzadas. En el Internet de las Cosas ideal, los dispositivos móviles serán capaces de recoger e interpretar datos como tu localización y preferencias conocidas, y comunicará con "objetos inteligentes"- sin requerir ninguna entrada.
El amplio rango de posibles futuras aplicaciones para el Internet de las Cosas incluye:
- Medios
- Mientras conduces más allá de una cartelera en la carretera o miras un anuncio en la televisión, los datos recogidos por tus dispositivos muestran que te gusta el tipo de producto que se está anunciando y se te envía automáticamente un mensaje con más información.
- Transportes
- Tu automóvil no solo puede aparcar en paralelo, sino que puede navegar y conducir por si mismo. Mejoras parecidas en trenes y aviones son solo algunas de las formas en que IoT podrá ayudarnos a medida que la tecnología progrese.
- Salud
- Los dispositivos médicos administrarán medicaciones automáticamente y monitorizarán las condiciones de los pacientes así como su estado general. Los marcapasos, ayudas a la audición y monitores cardíacos simplificarán el cuidado médico comunicando con los doctores y los pacientes.
- Infraestructuras
- Los sensores IoT monitorizan la estabilidad estructural de puentes, vías del tren y sistemas de gestión de desperdicios para su seguridad y protección.
Con el amplio uso de teléfonos inteligentes en nuestra sociedad, el Internet de las Cosas dispone de una fácil manera de recoger y utilizar datos personales para comunicarse con los objetos y dispositivos inteligentes. Pero para conseguir un salto inicial que haga posible IoT, necesitamos crear la próxima generación de tecnología móvil para optimizar los teléfonos inteligentes.
Cuando 5G reemplace a 4G LTE...
5G es el apodo escogido para la próxima generación de comunicaciones inalámbricas, de la que cada diez años surje una nueva versión. 5G en estos momentos es solo un concepto, pero se espera que esté implementada hacia 2020- proporcionando a la industria móvil un montón de trabajo que hacer en muy poco tiempo.
La mayoría de los profesionales de las comunicaciones inalámbricas están de acuerdo en que cuando 5G reemplace a 4G LTE, deberá de resolver tres necesidades clave:
- Una latencia decreciente por debajo de un segundo.
- Incremento de velocidades de datos de al menos un gigabit por segundo para decenas de miles de usuarios simultáneamente.
- Eficiencia energética mejorada.
Cualquiera que sean las mejoras que se hagan en las comunicaciones inalámbricas a la salida de 5G, el principal objetivo es que la tecnología móvil, la recogida de datos y las comunicaciones inalámbricas se integren mejor gracias a la velocidad y la eficiencia. Sin estas características, Internet de las Cosas no funcionará correctamente y será redundante.
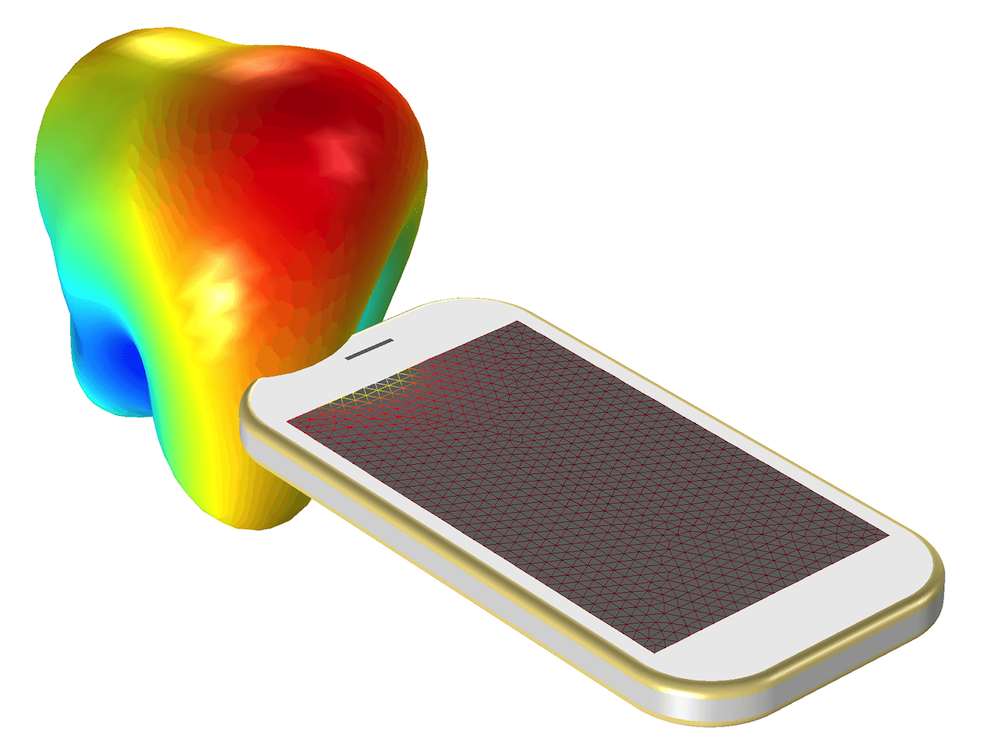
Entre los muchos desarrollos investigados en todo el mundo que ya están trabajando en 5G, la optimización de las antenas de los dispositivos móviles es un importante tema de estudio. Aunque las aplicaciones 5G todavía no se han estandarizado y muchos investigadores están desarrollando un conjunto de dispositivos para ampliar el mundo de IoT, podemos empezar echando un vistazo a un básico modelo introductorio que muestra cómo diseñar una pequeña antena en un dispositivo móvil en el tutorial de COMSOL Multiphysics "Modeling of a Mobile Device Antenna".
- Detalles
- Categoría: Comsol
- Visto: 3927
Ya está disponible COMSOL 5.1 Update 2 para COMSOL Multiphysics, que incluye Application Builder, COMSOL Server, y los módulos complementarios. En esta actualización acumulativa se han corregido algunos errores y ampliado las librerías de aplicaciones y ahora incluyen 26 apps de demostración únicas. A continuación se muestra una lista de las nuevas apps añadidas en Update 2:
- Fluid Flow of an Inkjet Nozzle Application: En los módulo CFD Module y Microfluidics Module. Esta aplicación demuestra cómo modelar el flujo de fluido de un cabezal de inyector de tinta, por ejemplo, de una impresora.
- Microstructure Thermal Material Property Calculator: En el módulo Heat Transfer. Calcula las propiedades térmicas equivalentes de materiales compuestos de microestructuras periódicas.
- Solar Irradiation Application: En el módlo Heat Transfer Module. La aplicación simula la irradiación solar en una playa con unas latas de bebida helada metidas en dos enfriadores bajo una sombrilla.
- Microresistor Beam Simulator: En el módulo MEMS Module. La aplicación simula el movimiento de una viga al correr una corriente a través de ella para generar un incremento de la temperatura, lo que lleva a un desplazamiento por expansión térmica.
- Mixing Efficiency Calculator: En el Mixer Module. La aplicación calcula la eficiencia del proceso de mezcla para mezcladores equipados con impulsores axiales o radiales.
- Frequency Selective Surface Simulator: En el módulo RF. La aplicación simula una estructura periódica para una superficie selectiva en frecuencia (FSS) que se puede escoger entre cinco tipos de células unitarias incluídas.
Se recomienda a todos los usuarios en mantenimiento que apliquen esta actualización a sus instalaciones de COMSOL.
- Detalles
- Categoría: Minitab
- Visto: 432887
Los análisis de regresión generan una ecuación que describe la relación entre una o más variables predictoras y la variable de respuesta. Después de utilizar Minitab Statistical Software para ajustar un modelo de regresión, y verificar el ajuste comprobando los gráficos de residuos, se querrá interpretar los resultados. A continuación veremos cómo interpretar los p-valores y los coeficientes que aparecen en la salida de un análisis de regresión lineal.
¿Cómo interpreto los P-valores en el análisis de regresión lineal?
El p-valor para cada término comprueba la hipótesis nula de que el coeficiente es igual a cero (no tiene efecto). Un p-valor bajo (< 0.05) indica que puedes rechazar la hipótesis nula. En otras palabras, un predictor que tenga un p-valor bajo es probable que tenga una adición significativa a su modelo porque los cambios en el valor del predictor están relacionados con cambios en la variable de respuesta.
Recíprocamente, un p-valor grande (insignificante) sugiere que los cambios en el predictor no están asociados con cambios en la respuesta.
En la salida de más abajo, podemos ver que las variables predictor de Sur y Norte son significativas porque los p-valores de ambas son 0.000. sin embargo, el p-valor para Este (0.092) es mayor que el nivel alfa común de 0.05, que indica que no es estadísticamente significativo.
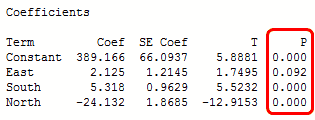
Típicamente se utilizan los p-valores para determinar que téminos deben de mantenerse en el modelo de regresión. En el modelo de arriba, deberíamos de considerar eliminar el Este.
¿Cómo interpretar los coeficientes de regresión para relaciones lineales?
Los coeficientes de regresión representan los cambios medios en la variable de respuesta para una unidad de cambio en la variable predictor mientras se mantienen constantes los otros predictores en el modelo. Este control estadístico que proporciona la regresión es importante porque aisla el plapel de una variable de todas las otras del modelo.
La clave para entender los coeficientes es pensar en ellos como pendientes, y a menudo se les llama coeficientes pendiente. Ilustraremos esto en el gráfico de línea ajustada de abajo, donde utilizamos la altura de las personas para modelar su peso. Primero, la ventana de la sesión de Minitab da:
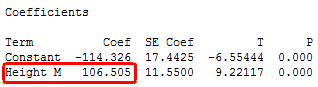
El gráfico de linea ajustada muestra los mismos resultados de la regresión en forma gráfica.
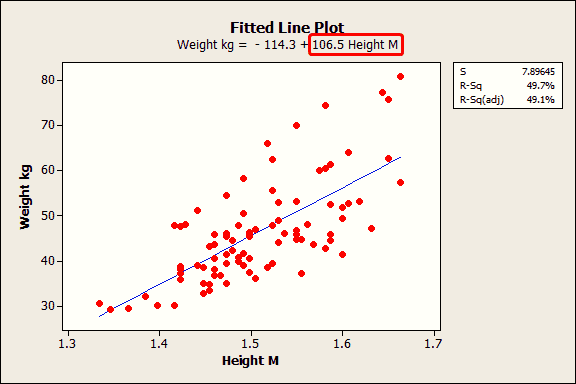
La ecuación muestra que el coeficiente para la altura en metros es 106.5 kilogramos. El coeficiente indica que para cada metro adicional en altura puedes esperar que el peso aumente en una media de 106.5 kilogramos.
La línea azul de ajuste muestra gráficamente la misma información. Si te mueves a la izquierda o derecha en el eje x en una cantidad que representa un cambio de un metro de altura, la línea de ajuste se incrementa o cae en 106.5 kilogramos. Sin embargo, estas alturas son para chicas en edad escolar y en un rango de 1.3 a 1.7 metros. La relación solo es válida dentro de este rango de datos, por lo que no sería real bajar o subir un metro por etá línea en todos los casos.
Si la linea de ajuste fuera plana (un coeficiente de pendiente cero), el valor esperado para el peso no cambiaría sin importar lo lejos que se fuera arriba o abajo de la línea. Así que, un p-valor bajo sugiere que la pendiente no es cero, lo que a su vez sugiere que los cambios en la variable predictor están asociados con cambios en la variable de respuesta.
Utilicé un gráfico de línea ajustada porque realmente trae las matemáticas a la vida. Sin embargo, los gráficos de línea ajustada solo pueden mostrar los resultados de regresiones simples, o sea una variable predictor y la respuesta. Los conceptos se mantienen ciertos para regresión lineal múltiple, pero se necesitarían dimensiones espaciales adicionales para cada predictor adicional para poder mostrar gráficamente los resultados. ¡Esto es difícil de mostrar con la tecnología actual!
¿Cómo interpreto los coeficientes de regresión para relaciones curvilíneas y los términos de interacción?
En el ejemplo anterior, la altura era un efecto lineal; la pendiente es constante, lo que indica que el efecto también es constante a lo largo de toda la línea ajustada. Sin embargo, si el modelo requiere términos polinomiales o de interacción, la interpretación es un poco menos intuitiva.
Como refresco, los términos polinomiales modelan la curvatura en los datos. Mientras que los términos de interacción indican que el efecto de un predictor depende del valor de otro predictor.
El siguiente ejemplo utiliza un conjunto de datos que requiere un término cuadrático para modelar la curvatura. En la salida de abajo, vemos que los p-valores para ambos términos, lienal y cuadrático, son significativos.
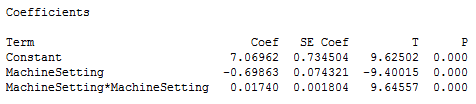
Los gráficos de residuos (no mostrados) indican un buen ejuste, así que podemos proceder con la interpretación. Pero, ¿como interpretamos estos coeficientes? Realmente ayuda graficarlos en un gráfico de línea ajustada.
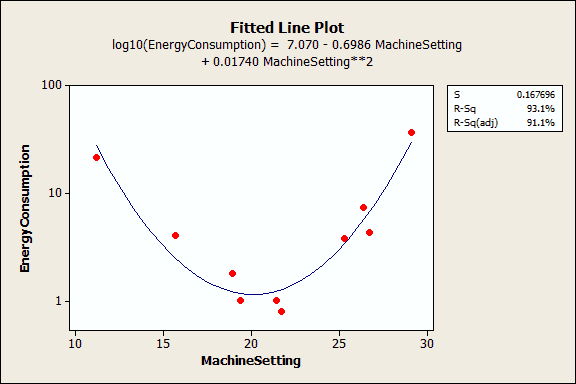
Se puede ver como la relación entre los ajustes de la máquina y el consumo de energía varía dependiendo de dónde se empiece sobre la línea ajustada. Por ejemplo, si se empieza en un ajuste de máquina de 12 y se incrementa el ajuste en 1, se esperará que el consumo de energía decrezca. Sin embargo, si se empieza en 25, un incremento de 1 debería incrementar el consumo de energía. Y si se está alrededor de 20, el consumo de energía no debería de cambiar demasiado.
Un término polinómico significativo puede hacer que la interpretación sea menos intuitiva porque el efecto de cambiar el predictor varía dependiendo del valor del predictor. De forma similar, un término de interacción significativo indica que el efecto del predictor varía dependiendo del valor de un predictor diferente.
Hay que tener mayor cuidado cuando se interpreta un modelo de regresión que contiene estos tipos de términos. Se puede mirar únicamente al efecto principal (término lineal) y comprender lo que está pasando. Desgraciadamente, si se está realizando un análisis de regresión múltiple, no se podrá utilizar un gráfico de línea ajustada para interpretar gráficamente los resultados. Esto es por lo que el conocimiento del área específica es un valor añadido.
- Detalles
- Categoría: Minitab
- Visto: 8713
Antes de unirme a Minitab, trabajé durante muchos años como escritor y editor en el Colegio Estatal de Pensilvania de Ciencias de la Agricultura. Escribía frecuentemente sobre ciencias alimentarias y, en particular, sobre seguridad alimentaria, ya que tenía que realizar informes regularmente sobre las investigaciones que se estaban llevando a cabo por los expertos en seguridad alimentaria del Estado de Pensilvania, y también editaba materiales para los cursos y boletines para profesionales y consumidores sobre como asegurar que disponían de una alimentación sana.
Después de unirme a Minitab y estár más familiarizado con los métodos de calidad basados en los datos como Seis Sigma, me sorprendió lo poco frecuentemente que algunas de las potentes herramientas de calidad típicas en muchas industrias son utilizaas en el trabajo de la seguridad alimentaria.
Así que me interesé por leer un reciente artículo en el sitio web Food Safety Tech sobre una aplicación de la herramienta llamada FMEA en el test de patógenos.
¿Qué es un FMEA?
El acrónimo FMEA viene del inglés "Failure Modes and Effects Analysis." Lo que realmente hace esta herramienta es ayudarte a examinar, cuidadosa y sistemáticamente, cómo y por qué exactamente las cosas pueden ir mal, de forma que puedas hacer todo lo posible para prevenir que esto ocurra.
En el artículo, Maureen Harte, un consultor y cinturón negro de Lean Six Sigma, habla sobre la necesidad de identificar, cuantificar y calcular los riesgos de diferentes métodos de detección de patógenos utilizados para crear un Certificado de Análisis (en inglés, Certificate of Analysis o COA)—un documento que obtienen las empresas para verificar la calidad y pureza de sus productos.
Demasiado amenudo, dice Harte, las empresas aceptan a ciegas los resultados del COA:
Les falta la información de fondo para realmente comprender lo que ocurre en el COA, y confían que lo que les viene es la máxima calidad.
Harte entonces explica como el desarrollar un FMEA puede hacer que el COA tenga más significado y utilidad.
FMEA nos ayuda a entender las diferencias entre los métodos de test identificando individualmente los riesgos asociados con cada método en sí mismo. Para cada paso del proceso [en un método de test], preguntamos: ¿Dónde podría fallar, y dónde podría ocurrir un error o modo de fallo? Lo escribimos en un papel y comprendemos cada uno de los modos de fallo.
Realizar un FMEA
Un FMEA normalmente se compone de estos pasos:
- Identificar los tipos de fallos potenciales, o "modos", para cada paso de tu proceso.
- Listar los efectos que resultan cuando ocurren esos fallos.
- Identificar las causas poteciales para cada modo de fallo.
- Listar los controles existentes que están realizándose para evitar que estos fallos ocurran.
- Valorar la severidad del efecto, la probabilidad de ocurrencia y las posibilidades de detección del modo de fallo antes de que cause perjuicios.
- Multiplicar los valores por severidad, ocurrencia y detección para obtener un número de prioridad de riesgo (RPN).
- Mejorar los ítems con un alto RPN, registrar las acciones que se lleven a cabo, entonces revisar el RPN.
- Mantenerlo como un documento vivo.
Se puede realizar un FMEA con lápiz y papel, pero las herramientas del software de mejora Quality Companion y Qeystone Tools de Minitab LLCluyen formularios que facilitan el desarrollo del FMEA—e incluso comparten datos dee mapas de procesos y otros formularios que se pueden estar utilizando.
- Detalles
- Categoría: Comsol
- Visto: 3798
El Rectorado de la Universidad de Málaga (UMA) acogió ayer, jueves 11 de junio, la segunda edición de la Iberian COMSOL Multiphysics Conference, una jornada científica organizada por la Escuela Politécnica Superior de la UMA, Addlink Software Científico S.L., COMSOL AB y la Fundación General de la UMA.
La segunda edición de este foro, que ha vuelto a celebrarse en Málaga, permite conectar a ingenieros y científicos españoles y portugueses involucrados en el modelado virtual de fenómenos físicos y que son usuarios de COMSOL Multiphysics. En esta ocasión ha reunido a unos cuarenta expertos, profesores e investigadores de empresas tecnológicas en simulación y modelado multifísico y se ha consolidado como un foro para el networking entre los especialistas en este campo, ya que permite poner en común diferentes trabajos de sistema de modelados desarrollados por la comunidad académica y de ingenieros.
 El acto de inauguración contó con la presencia de Emilio Ruiz Reina, profesor titular del departamento de Física Aplicada II de la Universidad de Málaga y miembro del Comité organizador del congreso; de Alejandro Rodríguez Gómez, director de la Escuela Politécnica Superior de la UMA; de Ed Fontes, director de tecnología de COMSOL; y de Juan Antonio Rubio, jefe de proyectos de Addlink Software Científico. Emilio Ruiz ha destacado que esta cita se ha convertido en un referente anual a nivel nacional entre los profesionales de este ámbito.
El acto de inauguración contó con la presencia de Emilio Ruiz Reina, profesor titular del departamento de Física Aplicada II de la Universidad de Málaga y miembro del Comité organizador del congreso; de Alejandro Rodríguez Gómez, director de la Escuela Politécnica Superior de la UMA; de Ed Fontes, director de tecnología de COMSOL; y de Juan Antonio Rubio, jefe de proyectos de Addlink Software Científico. Emilio Ruiz ha destacado que esta cita se ha convertido en un referente anual a nivel nacional entre los profesionales de este ámbito.
Además de las exposiciones de los trabajos que algunos de los asistentes han llevado a cabo con COMSOL Multiphysics, la jornada se ha completado con dos cursos de formación opcionales, uno de introducción que tuvo lugar el pasado miércoles 11 de junio y uno avanzado que tiene lugar hoy viernes.
- Detalles
- Categoría: Minitab
- Visto: 8534
Equilibrar los costes y la calidad puede ser un gran reto para cualquier fabricante. Pero es especialmente complicado para los que están involucrados en la asistencia médica, porque las herramientas utilizadas en los procedimientos médicos nunca deben verse comprometidas por los esfuerzos en reducir los gastos.
Pero reducir costes y asegurar el máximo de calidad no son mutuamente exclusivos. Por ejemplo, recientemente, Boston Scientific—uno de los líderes mundiales en el desarrollo de dispositivos y tecnologías médicas—ahorró tiempo y recursos y aseguró la fiabilidad de sus productos con un enfoque innovador en la validación de sus procesos.
Cuando una empresa externa transfirió la producción de un catéter de diagnóstico a sus instalaciones en Heredia, Costa Rica, Boston Scientific necesitaba demostrar que los catéteres producidos en la nueva localización serían igual de buenos. Pero el equipo del proyecto que gestionaba la transferencia tan solo tenía cuatro semanas para completar los requisitos del método de prueba necesarios para asegurar la aprobación de los reguladores—una fecha límite que no permitía validaciones extensas del método de prueba.
Así que, con la ayuda de Minitab Statistical Software, el equipo utilizó el análisis de datos para verificar que la fuerza del cable de tracción de los nuevos catéteres seguía cumpliendo las especificaciones utilizando la configuración de procesos ya existentes. Los resultados del equipo permitieron a Boston Scientific evitar la realización de una costosa validación del proceso, y permitió a la empresa continuar con sus planes de fabricación programados.
El reto
|
El catéter de diagnóstico se diseño para el seno coronario, una colección de venas del corazón. Los doctores lo utilizan durante los primeros procedimientos en pacientes de ataque cardíaco. El mango de este dispositivo tubular controla el cable de tracción, que manipula un cable plano que activa la punta del electrodo responsable de la curvatura de la herramienta. Este arco controla la estabilidad del catéter durante un procedimiento, haciendo que el "cable de tracción" sea fundamental para su éxito. Para garantizar el rendimiento del cable de tracción, se examina la fuerza de la soldadura que lo fija al mango aplicando tensión durante una prueba de tracción. Boston Scientific necesitaba demostrar, en la prueba de tensión, que los catéteres fabricados en las instalaciones de Heredia podían cumplir el rendimiento de los catéteres del fabricante original. Aunque la configuración de ambas empresas produjo catéteres que cumplían la especificación de fuerza del cable de tracción de 5 libras, todavía existían inconsistencias en las configuraciones de las pruebas de tracción de cada compañía. |
 El equipo en las instalaciones de Boston Scientific en Costa Rica utilizó Minitab Statistical Software para probar que la adaptación del proceso de pruebas de tensión del catéter no afectaría a los resultados de fuerza del cable de tracción. |
Una máquina de pruebas universal mide la fuerza de tracción aplicando cantidades crecientes de presión a un catéter sujetado entre dos mordazas. La distancia entre las dos mordazas, o longitud de referencia, difería en los métodos de prueba de las dos compañías, ya que la longitud de referencia de Boston Scientific se alineaba con el estándar de la ASTM (American Society for Testing and Materials) para la fuerza de tracción. Además, el catéter original se diseñó y aprobó en una época en la que no se requería la validación del método de prueba de los estándares del método de test específico. El equipo necesitaba comprobar que la diferencia en la longitud de referencia no comprometía la efectividad de las pruebas, y demostrar que ambos, el catéter nuevo y el original eran seguros y fiables. Podría ser necesario un proceso de validación del método de prueba extenso y costoso.
Para evitar incurrir en costes innecesarios, el equipo del proyecto se propuso comparar los resultados de la configuración de prueba del fabricante con los producidos por los estándares más rigurosos para las pruebas de tensión de Boston Scientific, y para demostrar de manera concluyente que la adaptación del proceso de pruebas de tensión del catéter no afectaría a la fuerza del cable de tracción. Si esto puediera mostrarse a la satisfacción de los reguladores, se reducirían tanto la cantidad de tiempo como el número de catéteres necesarios para completar la validación del método de pruebas aprovechando su estándar ASTM ya existente para las pruebas de tensión.
¿Cómo ayudó Minitab?
El equipo del proyecto decidió comparar la fuerza media del cable de tracción de la configuración de prueba de cada empresa utilizando un test t de 2 muestras. Para asegurar que los resultados del test fueran fiables, utilizaron las herramientas de Potencia (Power) y Tamaño de la Muestra (Sample Size) de Minitab y determinaron que necesitarían probar 23 catéteres con la configuracón de las pruebas de tensión de cada instalación.
El equipo reunió datos de pruebas de fuerza de una muestra aleatoria de 23 catéteres, probados con las normas ASTM, más rigurosas, para las pruebas de tensión de Boston Scientific y 23 catéteres probados con los ajustes de la prueba de tensión utilizadas por el fabricante original.
Ahora el equipo necesitaba verificar que los datos cumplían las dos asunciones a fin de producir resultados fiables. En primer lugar, de acuerdo con las directrices generales, cada muestra debería ajustarse a una distribución normal-un criterio que se comprobó con éxito utilizando los procedimientos estadísticos de Boston Scientific. En segundo lugar, debido a que la varianza de una muestra influye en su media, las muestras tenían que tener una varianza estadísticamente equivalente.
El menú de Estadísticas de Minitab proporciona herramientas fáciles de usar para evaluar estas dos condiciones para los datos. El equipo utilizó el test de 2 Varianzas para determinar rápidamente que sus datos cumplían los requisitos para un test t de 2 muestras.
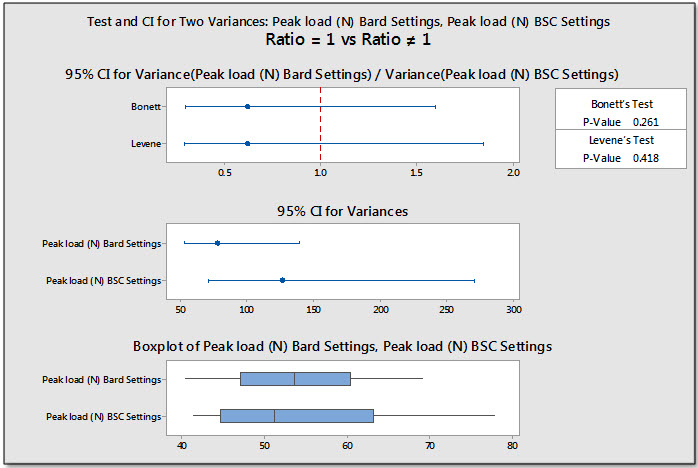
El gráfico mustra la varianza de cada conjunto de datos e ilustra que la diferencia entre ellas no es estadísticamente significativa.
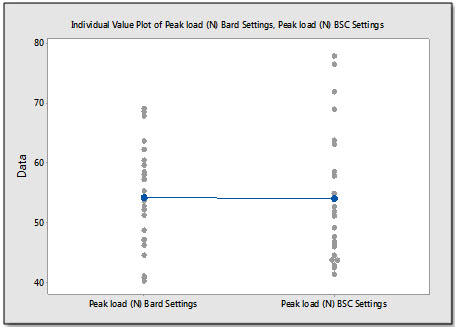
El gráfico de valores individuales muestra que, aunque la configuración de producción de Boston Scientific tiene un rango de resultados más amplio, las dos medias de la fuerza de tracción son prácticamente idénticas.
El test t de 2 muestras de Minitab mostró que las fuerzas de tracción no eran significativamente diferentes. Mientras realizaban el test t de 2 muestras, el equipo del proyecto encontró que la funcionalidad del asistente de Minitab—que proporciona explicaciones y recomendaciones bajo demanda además de una guía paso a paso—les proporcionaba más confianza en sus análisis y resultados. “A partir de los conocimientos proporcionados en el Asistente, aprendí que el cumplimiento de la asunción de normalidad para un test t de 2 muestras no es crítico cuando se tiene al menos 15 unidades para probar,” dijo German Vindas, ingeniero de fabricación de Boston Scientific. “Confirmó que nuestro tamaño de muestra de 23 unidades era más que adecuado, lo que nos proporcionó gran confianza en nuestros resultados.”
Resultados
El test t de 2 muestras del equipo demostró que las configuraciones de prueba de ambas compañías para la distancia de referencia producían fuerzas de tracción iguales, y los datos que recogieron mostraron que los cables de tracción en ambos conjuntos de catéteres cumplían el mínimo de 5 libras. Basándose en los resultados, los reguladores acordaron que Boston Scientific podía adaptar la validación del método de prueba del catéter aprovechando su estándar ASTM con la absoluta confianza de que la nueva fuerza de tensión del cable de tracción continuaría cumpliendo los estándares seguidos por el fabricante original.
Vindas estima que la utilización de las herramientas estadísticas de Minitab ahorró al equipo aproximadamente un mes en esta fase de la transferencia de la producción del catéter. El tiempo reducido empleado en esta fase redujo los costes de las pruebas a la vez que permitió a Boston Scientific cumplir los plazos del proyecto y pasar a la siguiente fase de las aprobaciones regulatorias de Costa Rica.
“Con Minitab, el proceso fue muy sencillo," dijo Vindas. “Nos ahorró montones de tiempo y dinero, y el proyecto pudo continuar en los plazos previstos.”
- Detalles
- Categoría: Comsol
- Visto: 14781
Por Caty Fairclough
Feliz cumpleaños al parisino "padre de la termodinámica", Nicolas Léonard Sadi Carnot. Un talentoso físico e ingeniero que canalizó su interés en los motores de vapor en la creación de un ciclo termodinámico teórico llamado el ciclo de Carnot. A través de esta teoría, Carnot sentó las bases de la segunda ley de la termodinámica, que se refiere a la entropía y la pérdida de calor y sigue siendo relevante en la física y la ingeniería actual.
Alimentando su pasión por los motores
Nicolas Léonard Sadi Carnot nació el 1 de junio de 1796 y ya mostró interés por las matemáticas a temprana edad. Su padre, Lazare Carnot, fue un líder del ejército revolucionario francés y tenía conocimientos de matemáticas e ingeniería que compartió con su hijo. Enseñó al joven Carnot ciencias, arte, lenguaje y música en su casa de París.

Un Carnot de diecisiete años vistiendo el uniforme de la École Polytechnique. (Por Louis-Léopold Boilly. Licenciada bajo dominio público, vía Wikimedia Commons).
Carnot estudió en la prestigiosa École Polytechnique, conocida por sus enseñanzas matemáticas y reputados profesores, entre los que se incluían Claude-Louis Navier y André-Marie Ampère. Durante su corta carrera académica Carnot fomentó un gran interés, de por vida, en resolver problemas de ingeniería. Después de graduarse, trabajó como ingeniero militar en el ejército francés, pero cambió de posiciones al sentirse descontento por la falta de oportunidades. Con el Cuerpo del Personal del General, Carnot fue capaz de dedicarle más tiempo a su interés personal por la ciencia y la ingeniería.
Tras la derrota de Napoleón en 1815, el padre de Carnot fue exiliado por su colaboración en la revolución. A pesar de ello, Lazare Carnot siguió alentando las actividades intelectuales de su hijo. Padre e hijo se mantuvieron en estrecho contacto y solían discutir sobre las máquinas de vapor. Carnot creía que la inferioridad de las máquinas de vapor francesas fue, en parte, responsable de la caída del reinado de Napoleón y por tanto también culpa del exilio de su padre y la pérdida de prestigio de su familia. Estaba muy motivado para aprender más sobre ellas.
El ciclo de Carnot y la termodinámica
Aunque las máquinas de vapor se utilizaron ampliamente en la época de Carnot, no existían teorías científicas sobre cómo funcionaban. Carnot se marcó el objetivo de llenar esta falta de información respondiendo a dos preguntas:
- ¿Existe límite en la cantidad de trabajo que una fuente de calor puede alcanzar?
- ¿Se puede mejorar una máquina de vapor reemplazando el vapor con otro fluido o gas?
Carnot recopiló sus ideas, y en 1824 publicó "Reflexiones sobre la potencia motriz del fuego", que contiene el famoso ciclo de Carnot. Su ciclo mantiene una alta eficiencia eliminando el estudio de fuerzas reales como la fricción y la conducción del calor entre la partes del motor a temperaturas variables. La eliminación de estos procesos es lo que hace que el ciclo de Carnot sea teórico y no realista.
El ciclo de Carnot funciona a través de la diferencia de temperatura entre dos depósitos. Durante el ciclo, el calor fluye (representado por Q1 y Q2) entre un depósito caliente, T1, y un depósito frío, T2. El motor de Carnot, C, se localizado en el centro de los depósitos. Cuando el calor fluye entre T1 y T2, el motor realiza trabajo, W, en el entorno circundante.
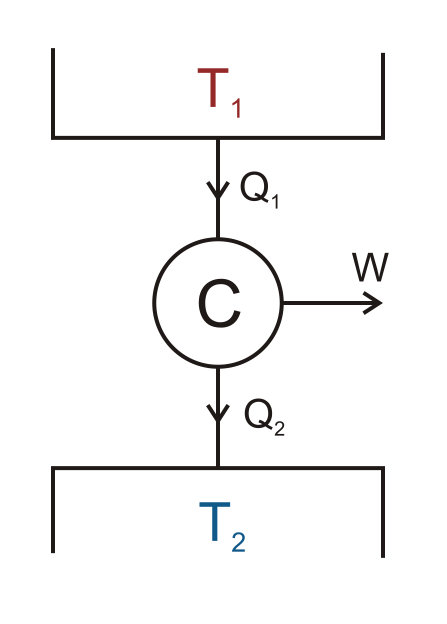
El ciclo de Carnot teórico. (“Esquema del motor de Carnot” por el propio trabajo de Keta. Licenciado bajo Creative Commons Attribution 2.5 Generic vía Wikimedia Commons).
Al crear este motor de vapor teórico, Carnot respondía a sus preguntas. Al analizar la cantidad de trabajo que un motor puede alcanzar, Carnot descubrió que para incrementar la eficiencia, había que reducir la pérdida de calor - específicamente, la pérdida de calor entre las partes del motor a diferentes temperaturas. A diferencia de su motor idealizado, siempre se pierde calor durante un ciclo en un motor real. Por este hecho, nunca puede alcanzarse una eficiencia perfecta fuera de las situaciones teóricas, y existe un límite en la cantidad de trabajo que una fuente de calor puede alcanzar.
Resolvió su pregunta sobre el reemplazo del vapor con otro fluido o gas comparando el aire y el vapor. Decidió que al eficiencia de un motor de calor ideal no dependía de la sustancia, sino de la diferencia de temperatura interna del motor.
Al responder estas preguntas, Carnot proporcionó ideas que más tarde fueron utilizadas en la creación de la segunda ley de termodinámica, que afirma que la entropía en nuestro universo aumenta con el tiempo y que los cambios en la entropía no pueden ser negativos.
Carnot murió durante una epidemia de cólera en 1832. Aunque muchos de sus escritos fueron enterrados con él, el trabajo restante de Carnot todavía contenía muchas nuevas ideas y conceptos. Sus contribuciones a la termodinámica siguen siendo fundamentales para los modernos científicos de hoy en día y le han hecho ser conocido como el "padre de la termodinámica".
El padre de la termodinámica en la era moderna
Las ideas de Carnot todavía son utilizadas para comprender y diseñar motores. Por ejemplo, al observar un motor o bomba de calor Stirling se puede analizar su eficiencia comparándolo con el ciclo de Carnot. Nosotros modelamos con COMSOL Multiphysics los cuatro pasos del ciclo de Carnot experimentados por un motor Stirling en otra entrada del blog de COMSOL. Como era de esperar, la eficiencia del motor modelado ni siquiera se acerca a la del ciclo de Carnot teórico.
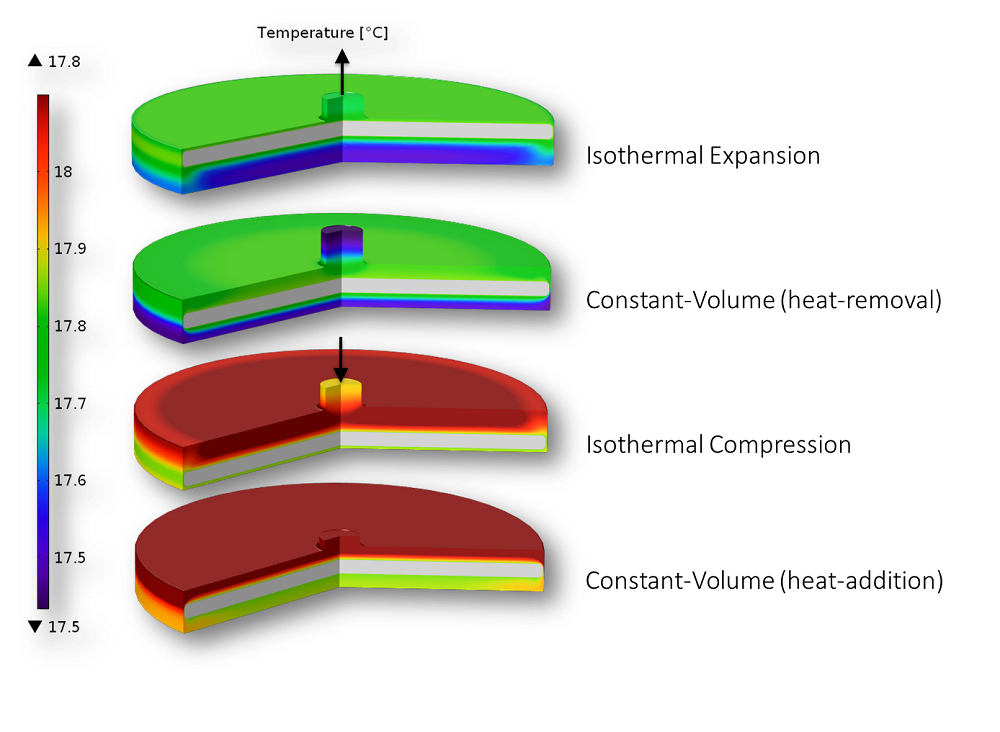
Los cuatro pasos del ciclo de Carnot: Procesos termodinámicos en un motor Stirling.
¡El 1 de junio deseamos a Nicolas Léonard Sadi Carnot, el padre de la termodinámica, un feliz cumpleaños!