Cómo la tecnología le ayuda a ayudar a sus estudiantes
Las matemáticas son importantes, tanto para el mundo en general como para el éxito futuro individual de sus estudiantes. Por eso, como educadores, se esfuerzan incansablemente por ayudar a sus estudiantes a comprender y trabajar con las matemáticas. Es una labor importante y gratificante, pero también una tarea desafiante que se vuelve especialmente difícil cuando el tamaño de las clases aumenta, las distracciones se multiplican y los efectos de la pérdida de aprendizaje se siguen sintiendo. Afortunadamente, la tecnología adecuada puede actuar como su asistente, rindiendo mejor el tiempo y la energía invertidos en la enseñanza y ayudándoles a alcanzar el éxito de sus estudiantes.
En este informe técnico, examinaremos siete desafíos extremadamente comunes que enfrentan los instructores de matemáticas y cursos que las utilizan, como ingeniería, física, química, negocios y economía. Para cada desafío, mostraremos ejemplos de cómo Maplesoft Mathematics Suite, una colección de soluciones de software de Maplesoft, puede proporcionar visualizaciones enriquecedoras, retroalimentación instantánea, ejemplos motivadores, exploraciones prácticas y otros recursos que pueden ayudarle a superar dicho desafío. Para ilustrar estos ejemplos, proporcionamos capturas de pantalla y breves videos tomados con diversos productos de la Suite.
Los desafíos
Cuando se trata de la enseñanza de las matemáticas, ya sea que enseñes un curso de matemáticas o un curso que se base en ellas, hay siete desafíos muy comunes que experimentan los educadores:
- Involucrar a los estudiantes que se aburren o distraen fácilmente
- Motivar a los estudiantes que no ven el sentido
- Superar la ansiedad matemática
- Inculcar una verdadera comprensión en los estudiantes que solo están siguiendo los pasos.
- Proporcionar suficientes oportunidades para la práctica
- Evaluar el progreso en un mundo donde es fácil buscar respuestas
- Gestión de diferentes niveles de preparación para el curso
No se pueden solucionar estos problemas dedicando más tiempo a las clases. ¿De dónde se obtendrían esas horas? Pero la tecnología matemática puede ayudar en cada una de estas áreas.
Desafío 1: Involucrar a los estudiantes que se aburren o distraen fácilmente
Los estudiantes tienen mucha demanda de atención, incluso en clase. Gran parte del contenido de sus teléfonos y portátiles está diseñado específicamente para distraerlos cuando se necesita que presten atención, y para muchos estudiantes, "un montón de ecuaciones" no es precisamente atractivo.
Pero las matemáticas pueden cobrar vida. Pueden ser visuales. Pueden ser interactivas. Puede ser divertido experimentar con ellas, simplemente para ver qué sucede. A veces, incluso pueden inspirar a los estudiantes con sus posibilidades. Pero para eso, se necesita más que una página estática. Se necesita algo dinámico, con visualizaciones ilustrativas e interactividad significativa.
|
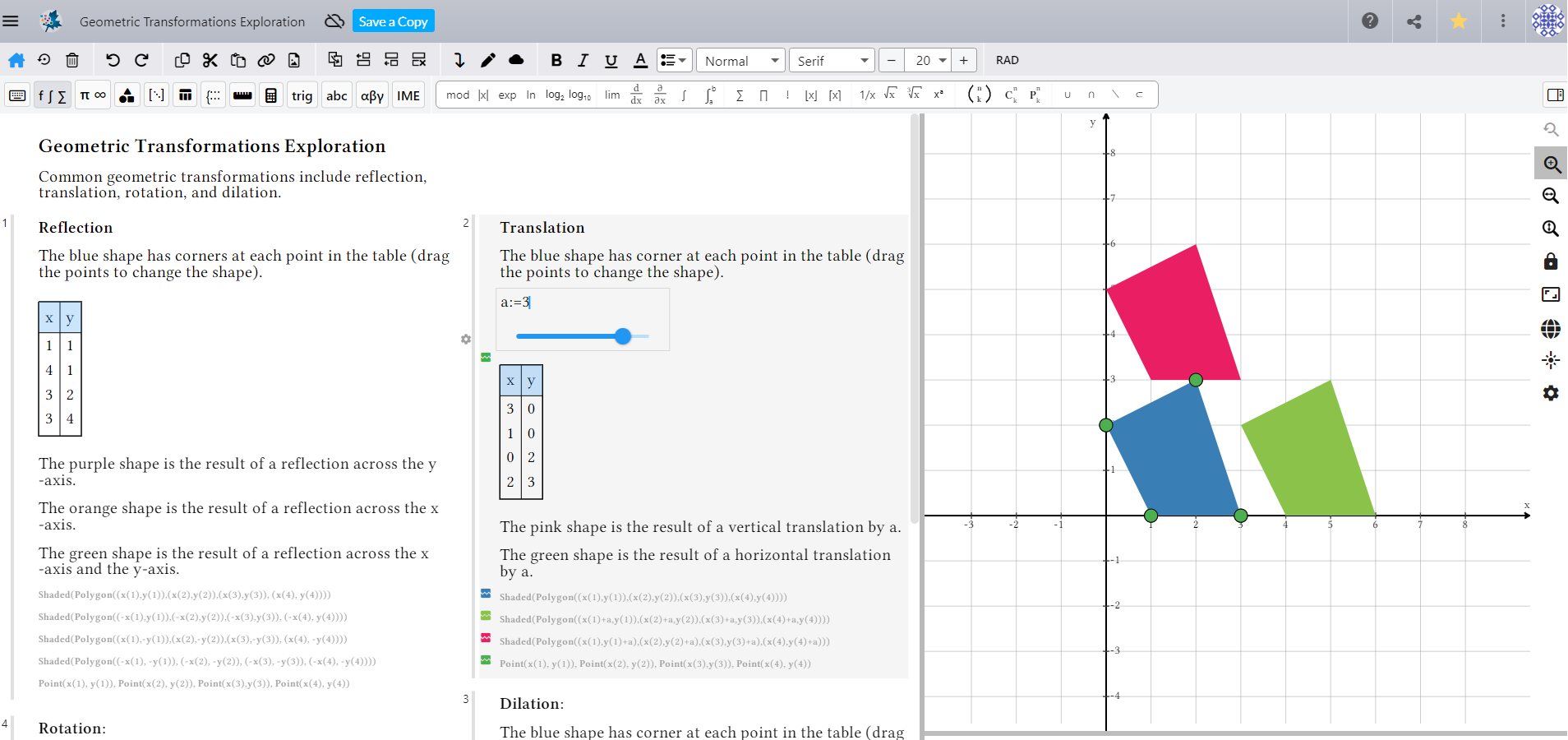
Ejemplo: Transformaciones geométricas En este ejemplo que demuestra transformaciones geométricas, los estudiantes pueden realizar reflexiones, rotaciones y dilataciones por sí mismos y ver los resultados al instante. Por ejemplo, pueden crear una figura y verla reflejada en los ejes x e y, trasladar una figura horizontal y verticalmente moviendo un control deslizante, o mover otro control deslizante para establecer un factor de dilatación y ver los resultados. |
|
|
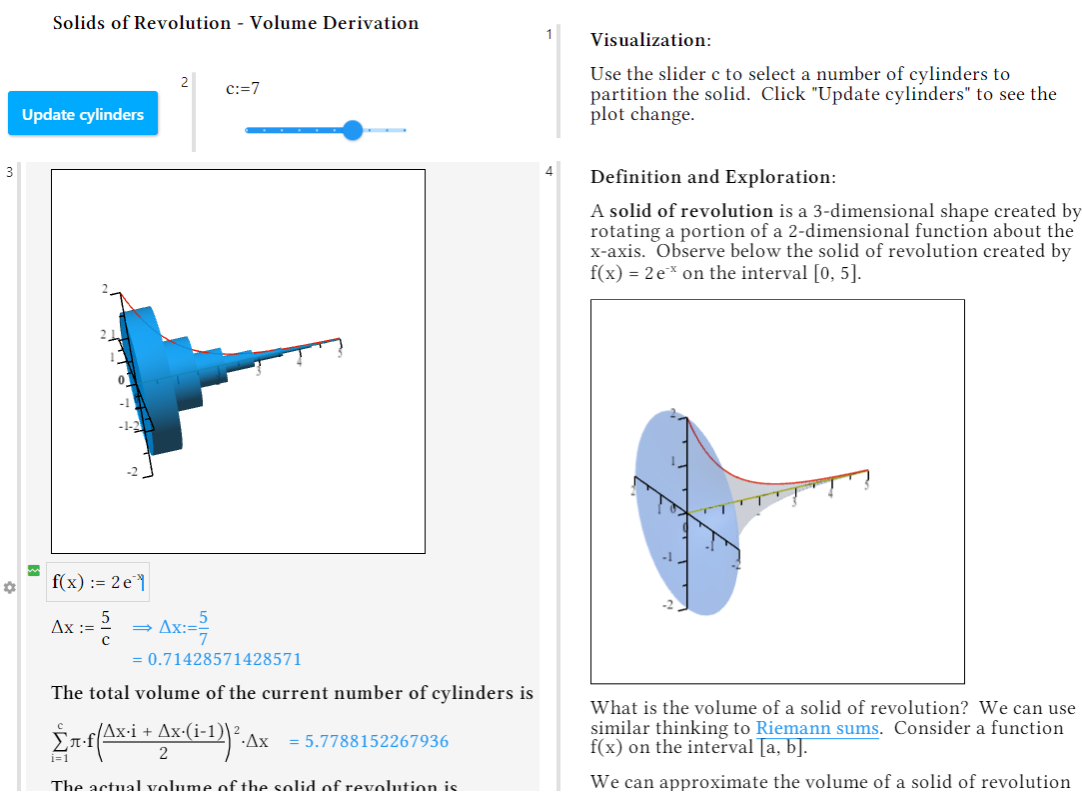
Ejemplo: Volumen de sólidos de revolución A los estudiantes a menudo les cuesta visualizar los sólidos de revolución, y los instructores se han retorcido hasta el cansancio intentando transmitir el concepto. En este ejemplo, los estudiantes pueden observar cómo se gira la curva 2D para formar la figura 3D y luego girar la imagen resultante para verla bien desde diferentes ángulos. Pueden observar cómo los cilindros se aproximan a la figura y aumentar el número de cilindros para comprobar, tanto visual como numéricamente, cómo mejora la aproximación. |
|
Desafío 2: Motivar a los estudiantes que no ven el sentido
Seguramente ha escuchado muchas variaciones de "¿Pero para qué sirve esto?" en clase. Algunos estudiantes pueden estar encantados de aprender matemáticas por el simple hecho de aprenderlas, pero la mayoría quiere saber por qué necesitan aprender lo que les estás enseñando. ¿Para qué sirve? ¿Por qué debería importarle a alguien?
Por supuesto, las matemáticas se usan en todas partes, y sus aplicaciones prácticas contribuyen enormemente a motivar a los estudiantes. Desafortunadamente, la mayoría de los ejemplos realistas son demasiado complicados para resolverlos en clase a mano, y a veces involucran matemáticas que los estudiantes aún no han aprendido. Pero con la tecnología adecuada, puede presentar a sus estudiantes aplicaciones motivadoras de los conceptos que necesita que aprendan, sin que nadie se atasque en los cálculos.
|
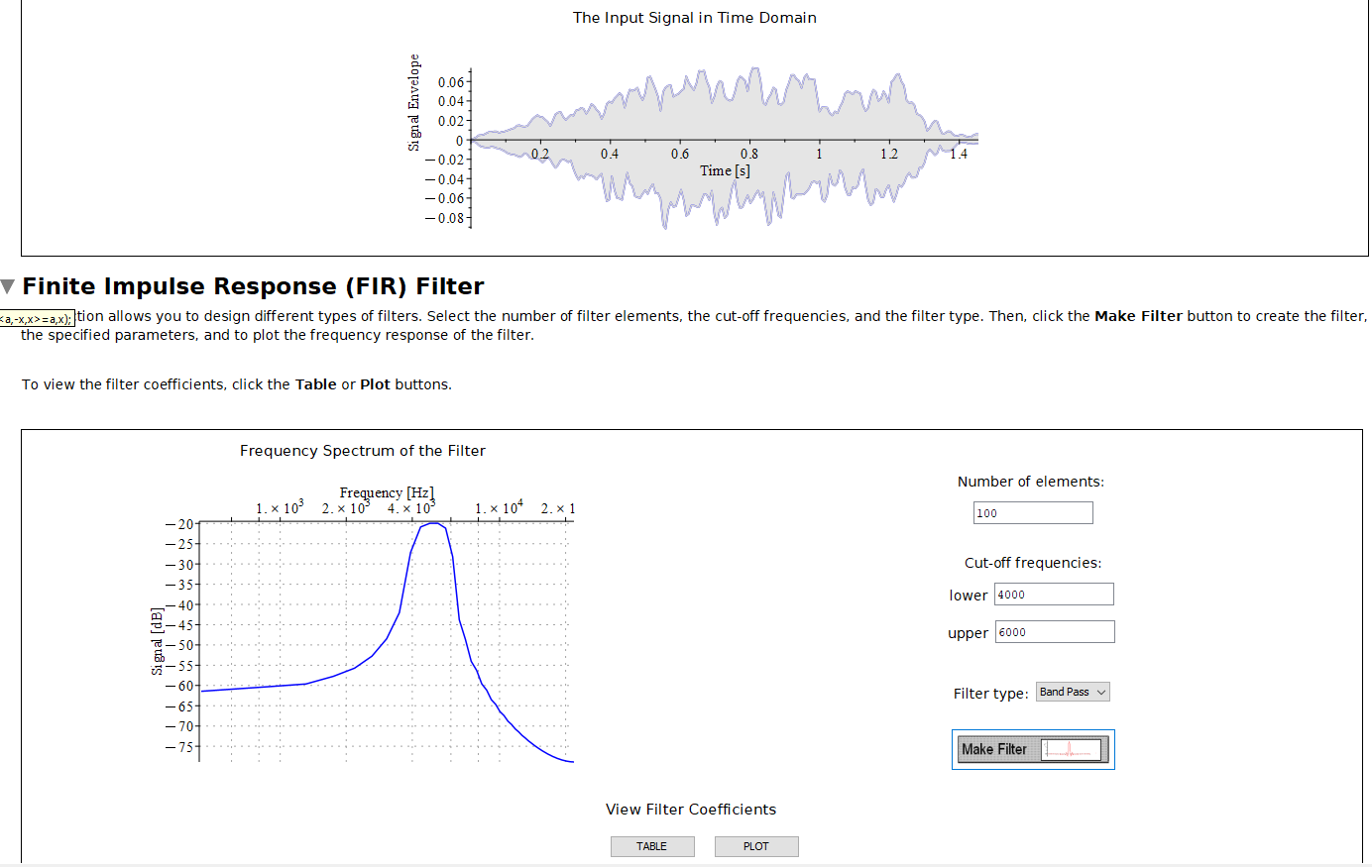
Ejemplo: Diseño de filtros digitales Las transformadas de Fourier y las transformadas rápidas de Fourier pueden parecer manipulaciones engorrosas, y puede ser difícil transmitir su importancia de forma tangible para los estudiantes. Sin embargo, casi todos los estudiantes han escuchado audio con sonido borroso en algún momento. En este ejemplo, los estudiantes diseñan filtros de Respuesta de Impulso Finito (FIR) para eliminar el ruido de un archivo de audio que pueden generar ellos mismos. Pueden experimentar con los diferentes tipos y configuraciones de filtros sin tener que lidiar aún con los cálculos, y ver, e incluso escuchar, los resultados por sí mismos. Al final, los estudiantes adquieren una comprensión más intuitiva de lo que significa eliminar el ruido de una señal, experimentan la necesidad de diferentes tipos de filtros para señales con diferentes características, tienen una mejor comprensión conceptual y una mayor motivación para aprender las matemáticas que lo sustentan. |
|
Desafío 3: Superar la ansiedad matemática
Algunos estudiantes llegan a clase ansiosos y estresados antes de que puedas siquiera abrir la boca. La ansiedad matemática inhibe su capacidad de aprendizaje, pero no hay suficientes horas a la semana para dedicarles mucha atención extra. Sin embargo, puedes usar la tecnología para ayudar a mejorar su confianza:
- Ayudándoles a identificar las habilidades que ya tienen
- Dándoles herramientas a las que puedan recurrir cuando se queden atascados.
- Mostrándoles dónde se equivocaron y cómo solucionarlo.
|
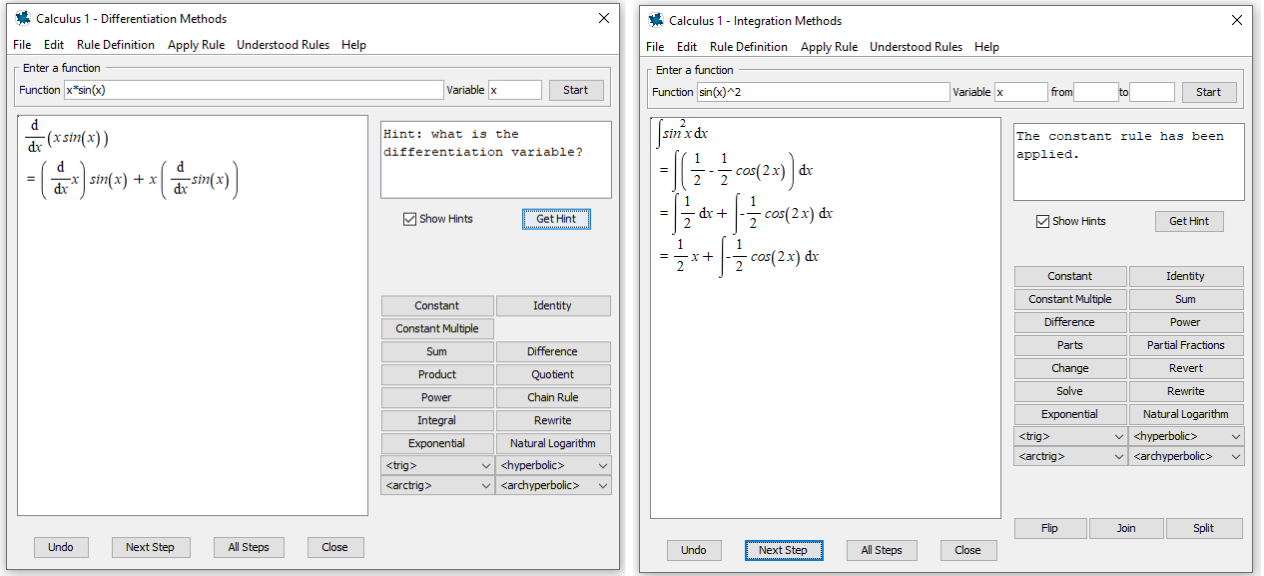
Ejemplo: comprobar cada línea de una solución trabajada El estudiante resuelve una integral en papel. Luego, solicita la solución a una herramienta matemática y, si la respuesta es correcta, se tranquiliza y se siente un poco menos ansioso. Si descubre que su respuesta es incorrecta, el estudiante ansioso suele asumir que simplemente "no lo entiende", lo que refuerza la ansiedad y la inseguridad. Pero en lugar de detenerse ahí, el estudiante puede tomar una foto de su trabajo con una aplicación de matemáticas en su teléfono y subir la solución completa a una herramienta en línea. Allí, puede pedirle a la herramienta que revise la solución línea por línea, y esta identifica dónde cometió el error. De esta manera, el estudiante ve dónde se equivocó y cuánto acertó. Si fue un pequeño error, recupera la confianza en su comprensión conceptual. Si necesita ayuda, ahora tiene una pregunta más precisa, lo que facilita mucho que su instructor, amigo u otra persona le ayude rápidamente, reduciendo el tiempo que el estudiante pasa sintiéndose ansioso. |
|
|
Ejemplo: Práctica de diferenciación e integración El estudiante ansioso tiende a ver cada respuesta incorrecta como una señal de que no entiende nada. Darle la oportunidad de practicar los conceptos por separado de los cálculos ayuda a reforzar las ideas importantes sin la ansiedad injustificada causada por errores simples. También le muestra al estudiante cuánto realmente entiende, para que pueda mantener la calma más tarde cuando falta un signo menos. En este ejemplo, estas herramientas ayudan al estudiante a practicar las reglas de diferenciación e integración, con un enfoque en comprender cuándo aplicar cada método. El estudiante elige qué paso aplicar, y la herramienta realiza los cálculos reales para que el estudiante pueda mantenerse enfocado en comprender cómo resolver problemas a un nivel superior. Si tiene dificultades, el tutor le da una pista si el estudiante comete un error, y el estudiante puede pedir una pista o el siguiente paso, para que nunca se atasque por completo ni se desanime. |
|
Desafío 4: Inculcar una verdadera comprensión en estudiantes que solo siguen el ritmo
Algunos estudiantes pueden imitar lo que aprenden en clase, pero no comprenden realmente qué hacen ni por qué. Siguen los pasos y llegan a una solución, pero simplemente siguen el procedimiento. Si cambias ligeramente el tipo de problema, o no lo notarán o no sabrán qué hacer. Quieres que tus estudiantes realmente comprendan lo que hacen, no que apliquen un algoritmo a ciegas.
En muchos casos, una buena manera de lograr el objetivo de comprensión es ayudar a los estudiantes a visualizar los conceptos detrás de los pasos, y la tecnología puede ayudarle a hacerlo.
|
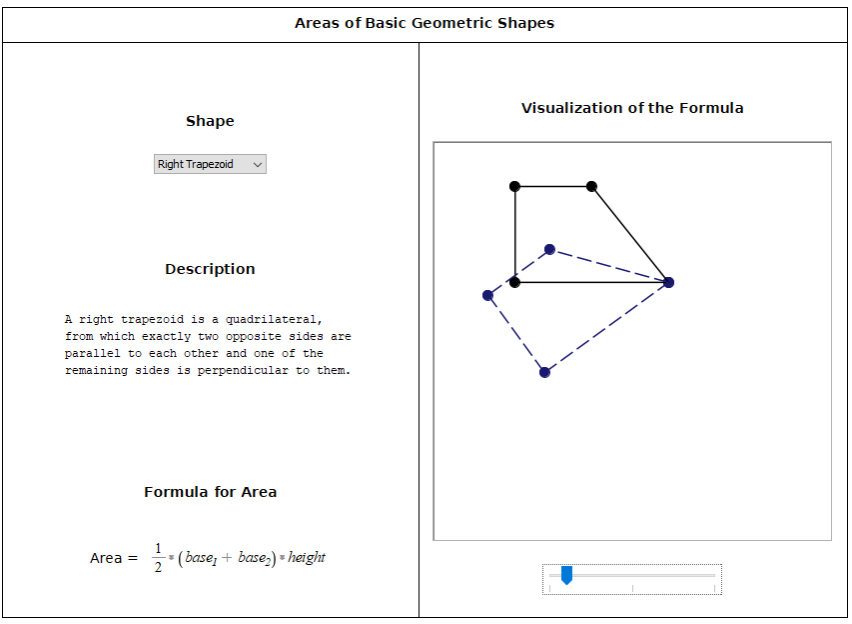
Ejemplo: Fórmulas de área de figuras geométricas básicas En esta aplicación, los estudiantes pueden animar la construcción geométrica detrás de la fórmula del área de una figura dada. Ahora, en lugar de memorizar un montón de fórmulas aparentemente aleatorias, pueden ver de dónde provienen, lo que les ayudará a recordarlas y les proporcionará técnicas para abordar problemas más complejos. Ver: Comprensión de las fórmulas de área de figuras geométricas |
|
|
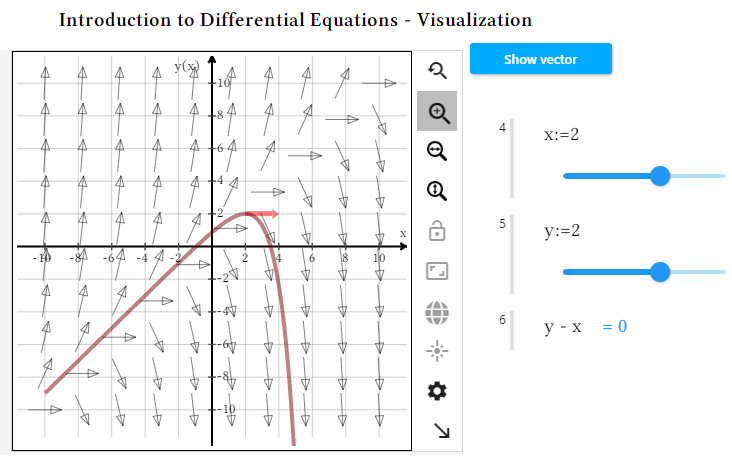
Ejemplo: Comprensión de ecuaciones diferenciales Una cosa es seguir los pasos para resolver una ecuación diferencial, pero otra muy distinta es comprender qué sucede realmente y por qué existen soluciones generales y particulares. En este ejemplo, los estudiantes ven un campo de direcciones para la ecuación diferencial elegida, la flecha de dirección en un punto específico y cómo la traza de una solución aproximada que pasa por ese punto sigue las flechas. Pueden experimentar seleccionando diferentes puntos y observando cómo cambian el vector y la solución en cada caso. Desarrollar su comprensión intuitiva mediante este tipo de exploración proporciona a los estudiantes una base sólida sobre la que desarrollar nuevas habilidades. |
|
Desafío 5: Brindar suficientes oportunidades para la práctica
Las visualizaciones que promueven la comprensión conceptual son importantes, pero también es necesario que los estudiantes se pongan manos a la obra y empiecen a resolver problemas. Hay muchísimos. Pero el libro de texto tiene un número limitado de problemas con soluciones, y a menudo, eso no será suficiente práctica para algunos estudiantes.
Con la tecnología adecuada, los estudiantes tienen acceso a un conjunto inagotable de ejercicios de práctica que les permiten practicar tanto como necesiten. La herramienta les indicará si aciertan o no, para que puedan ganar confianza a medida que desarrollan sus habilidades. Mejor aún, algunas herramientas pueden incluso ayudarles a comprender dónde se equivocaron y cómo retomar el rumbo.
|
Ejemplo: Práctica para hallar derivadas: reglas del producto y del cociente En este ejemplo, la herramienta genera una secuencia de ejercicios de práctica diseñados para que los estudiantes practiquen un conjunto muy específico de habilidades: aplicar las reglas del producto y el cociente para hallar derivadas. El estudiante primero resuelve el ejercicio en papel, luego usa una aplicación de matemáticas en su teléfono para tomar una foto y subirla a la herramienta, y hace clic en "Verificar trabajo". La herramienta examina cada línea de su solución y, en este caso, le indica al estudiante que cometió un error en el penúltimo paso. El estudiante entonces ve que aplicó las reglas correctamente, pero cometió un error aritmético en su derivación. Corrige el error en el documento, lo vuelve a revisar y luego pasa al siguiente ejercicio. El estudiante también puede pedir sugerencias y, como el instructor lo permite, puede solicitar ver la solución completa cuando necesite otro ejemplo para comprender mejor. Ver: Práctica: Hallar derivadas usando las reglas del producto y el cociente |
|
|
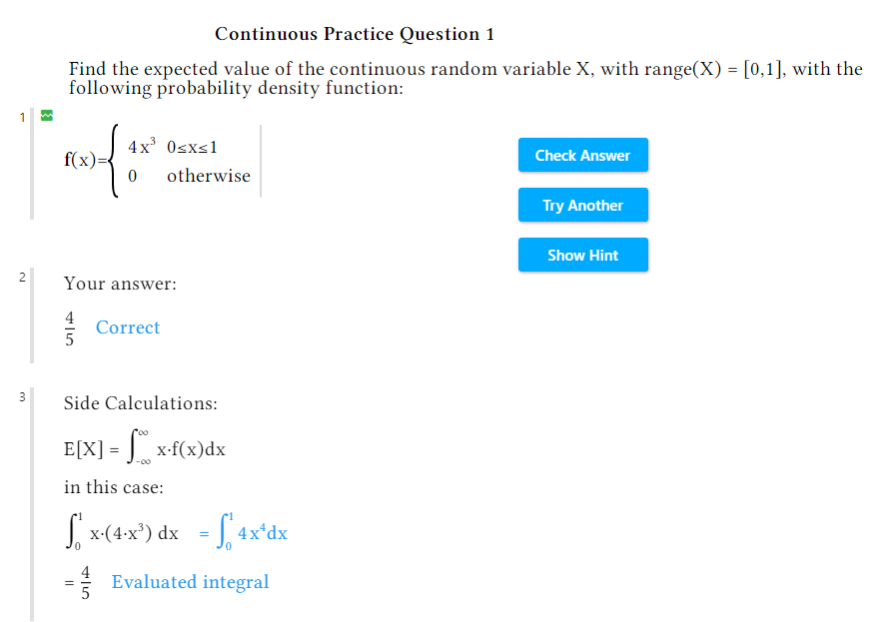
Ejemplo: Valor esperado Este documento genera preguntas que permiten a los estudiantes practicar la búsqueda del valor esperado de una variable aleatoria continua y luego comprobar sus respuestas. Primero, los estudiantes encuentran la solución dentro del documento, combinando pasos manuales y cálculos realizados por la herramienta. En este caso, el instructor optó por no incluir la opción de ver las soluciones completas, pero sí ofreció sugerencias. |
|
Desafío 6: Evaluar el progreso en un mundo donde es fácil buscar respuestas
Hoy en día, sus estudiantes pueden obtener respuestas fácilmente a las preguntas típicas del tipo "Resuelve esto", independientemente de si entienden lo que están haciendo o no. Puede comprender mucho mejor el aprendizaje de sus estudiantes al asignarles tareas y proyectos centrados en la resolución de problemas conceptuales. A menudo, estos proyectos implican una combinación de comprobación de hipótesis, visualización, explicaciones escritas, cálculos que desea que realicen por sí mismos y cálculos de los que no desea que tengan que preocuparse. La plataforma tecnológica adecuada puede brindarle el entorno necesario para crear proyectos interesantes que sus estudiantes no pueden realizar simplemente buscando respuestas. En cambio, necesitan pensar, cuestionar, comunicarse y aprender.
|
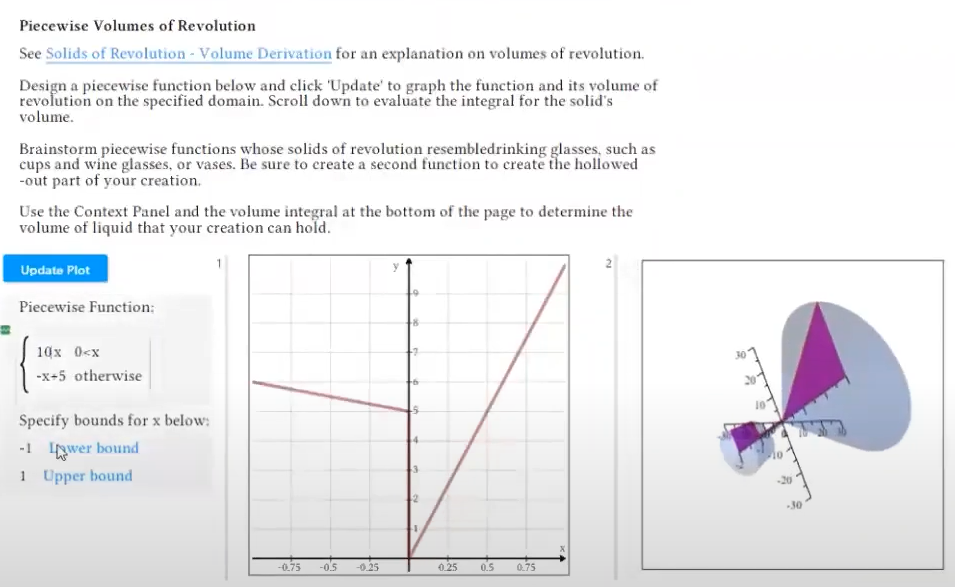
Ejemplo: Sólidos de revolución En este proyecto, se reta a los estudiantes a crear una función a trozos cuyo sólido de revolución se parezca a una copa de vino o un jarrón. Pueden probar varias funciones, con diferentes límites superiores e inferiores, y observar los resultados. Rápidamente, empiezan a pensar en cómo deberían modificar la función para obtener una forma más atractiva. El instructor también puede establecer un requisito para el volumen mínimo o máximo del recipiente, y los estudiantes pueden usar el software para configurar y resolver la integral y determinar el volumen de cada figura, y luego realizar ajustes adicionales a su función para refinar su vaso o jarrón. En el mismo entorno, el instructor puede pedir a los estudiantes que respondan preguntas que les obliguen a comunicar sus reflexiones y procesos de pensamiento. Ver: Proyecto: Diseña una copa de vino con sólidos de revolución |
|
Desafío 7: Gestionar distintos niveles de preparación para el curso
Los estudiantes ingresan a tu clase con diferentes antecedentes y distintos niveles de preparación. Quieres ayudar a los estudiantes menos preparados a alcanzar a sus compañeros y tener éxito, pero no hay tiempo para brindarles ayuda individualizada. Y eso sin siquiera pensar en los estudiantes más avanzados, a quienes te gustaría mantener motivados y fomentar sus habilidades e interés en la materia. Sin embargo, un buen repositorio de contenido interactivo listo para usar, que cubra diferentes temas y niveles, significa que los estudiantes con diferentes necesidades tienen acceso a materiales que les ayudarán a aprender por sí mismos. Y cuando ese contenido se puede personalizar fácilmente, puedes usarlo como punto de partida para desarrollar recursos más específicos, para el autoaprendizaje, demostraciones en clase, proyectos o lo que necesites.
|
Ejemplo: Recursos de contenido El contenido y las herramientas para ayudar a los estudiantes a utilizar las soluciones de Maplesoft Mathematics Suite incluyen:
|
|