Modelado basado en ecuaciones en COMSOL Multiphysics
- Detalles
- Categoría: Comsol
- Visto: 10215
Todos los que hemos pasado por escuelas de ingeniería hemo sido formados en la física y el cálculo prácticamente a la vez. Es lógico, ya que las ecuaciones matemáticas son la base fundamental para poder interpretar cualquier fenómeno físico.
Las destacan en gran medida por su caracter aplicado, debido a que la mayor parte de los fenómenos que ocurren en la naturaleza cambian con el tiempo, y como vivimos en un espacio 3D, las ecuaciones diferenciales parciales (que expresan el cambio en más de una dirección) surgen como una herramienta de gran importancia para expresar la física a nivel continuo para propósitos de ingeniería.
La inmensa mayoría de estas ecuaciones deben sus nombres a personalidades científicas de la ciencia tecnológica aplicada, como o , primeros pioneros que demostraron y promovieron en gran medida la interpretación de los fenómenos naturales a través de sus ecuaciones y con los que, tanto ingenieros como científicos tenemos una gran deuda. Tras ellos surgieron modelos matemáticos asociados a diferentes fenómenos de la Física (, , ...), Química (procesos de ), Biología (estudio de especies biológicas), Óptica (procesos de difusión de la luz), Estadística (), Economía (optimización del rendimiento), Ingeniería (diseño óptimo de ) por citar algunos ejemplos de la larga lista.
Pero no a todo el mundo le gustan la ecuaciones. De hecho muchos ingenieros lo son a pesar de las ecuaciones. Las quejas más comunes son que las ecuaciones son demasiado abstractas, complicadas y aburridas. Tienen poco que ver con el hecho de poner "cosas" juntas y hacer que funcionen, lo que forma una gran parte del método en ingeniería. Sin embargo, por otro lado podemos encontrar algunos ingenieros que son expertos teóricos y que se encuentran mucho más cómodos con las ecuaciones que con la cosa real que están haciendo o mejorando. En realidad, en cualquier organización de ingeniería, es probable encontrar ambos tipos de profesionales.
Por suerte COMSOL favorece ambos puntos de vista. Si se está más cómodo describiendo los fenómenos en términos de la física: cargas, restricciones, campos, conductividad, corrientes, etc. COMSOL permite utilizar terminología especializada específica para el tipo de aplicación. Esto se aplica a todo, desde las propiedades del material, a las condiciones de contorno y otras variables del modelo.
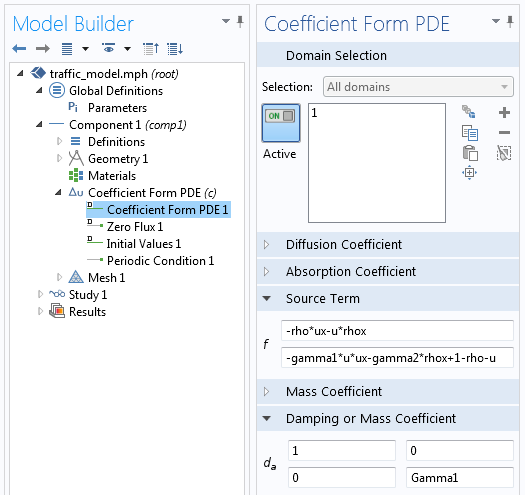
O bien, se puede ser del tipo que piensa que es mejor ver la ecuación y desentrañar lo que está describiendo. Para ellos se dispone de una sección en la ventana de ajustes (oculto para nadie se asuste de antemano). Esta opción abre la caja negra de la simulación y revela exactamente el sistema de ecuaciones que se está resolviendo.
El objetivo de COMSOL es hacer que el modelado multifísico sea accesible a todos los ingenieros serios, tanto investigadores como diseñadores o en producción.
Otra de las potentes posibilidades que ofrece COMSOL Multiphysics es la de ir más allá, gracias a su capacidad de realizar modelado basado en ecuaciones. El puede acceder fácilmente a las ecuaciones que describen la física con la que está trabajando y añadir términos o manipularlas como mejor le parezca. Algo que, sin duda, abre drásticamente las posibilidades que se pueden alcanzar a través del modelado y la simulación.
Puede acceder a una serie de para ver cómo los usuarios pueden acceder a las ecuaciones y añadir sus propias ecuaciones en derivadas parciales desde la interfaz de COMSOL Multiphysics.
Si quiere aprender más sobre el tema participe en el próximo seminario del 1 de junio que tendrá lugar en Bilbao.

